Функция 1 2 y x четная потому что
Четные и нечетные функции
Вы будете перенаправлены на Автор24
Четные функции
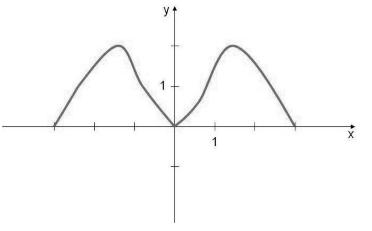
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
Нечетные функции
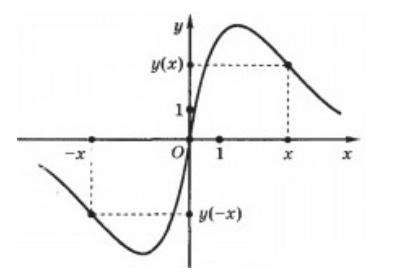
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
Готовые работы на аналогичную тему
Функция общего вида
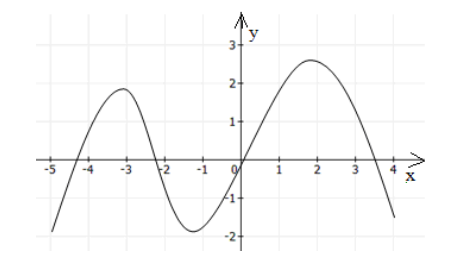
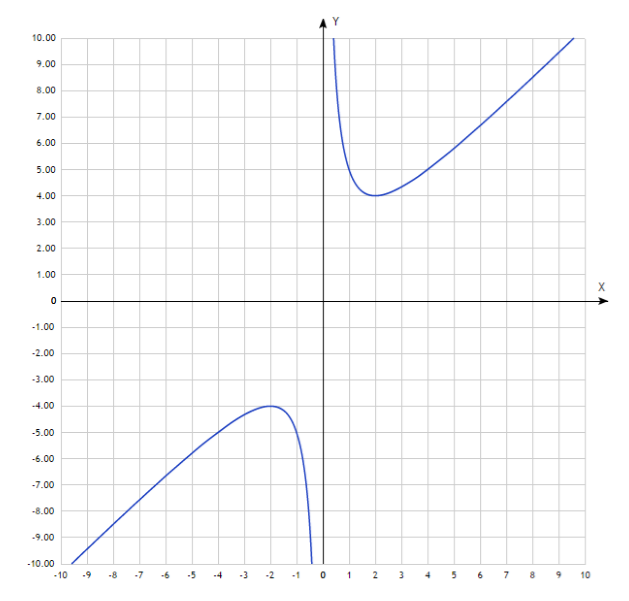
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
Пример задачи
Исследовать функцию на четность и нечетность и построить их графики.
Изобразим её на графике:
Изобразим её на графике:
Изобразим её на графике:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 07 2021
Четность и нечетность функции. Период функции. Экстремумы функции
Содержание
Способы задания функции
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Четная и нечетная функция
Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.
Исследуем на четность нижеприведенную функцию:
Значит, функция f(x)=3x^<3>-7x^ <7>является нечетной.
Периодическая функция
f(x) > 0 на (x_<1>; x_<2>) \cup (x_<3>; +\infty )
f(x) на (-\infty; x_ <1>) \cup (x_<2>; x_ <3>)
Ограниченность функции
Возрастающая и убывающая функция
Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0 ).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
Экстремумы функции
Необходимое условие
Достаточное условие
Наибольшее и наименьшее значение функции на промежутке
Квадратичная функция.
Обратите внимание: коэффициент a может быть любым действительным числом, кроме нуля. Действительно, если a = 0, то ax 2 + bx + c = 0·x 2 + bx + c = 0 + bx + c = bx + c. В этом случае в выражении не остаётся квадрата, поэтому его нельзя считать квадратным трёхчленом. Однако, такие выражения-двучлены как, например, 3x 2 − 2x или x 2 + 5 можно рассматривать как квадратные трёхчлены, если дополнить их недостающими одночленами с нулевыми коэффициентами: 3x 2 − 2x = 3x 2 − 2x + 0 и x 2 + 5 = x 2 + 0x + 5.
Если стоит задача, определить значения переменной х, при которых квадратный трёхчлен принимает нулевые значения, т.е. ax 2 + bx + c = 0, то имеем квадратное уравнение.
Если существуют действительные корни x1 и x2 некоторого квадратного уравнения, то соответствующий трёхчлен можно разложить на линейные множители: ax 2 + bx + c = a(x − x1)(x − x2)
Замечание: Если квадратный трёхчлен рассматривать на множестве комплексных чисел С, которое, возможно, вы еще не изучали, то на линейные множители его можно разложить всегда.
Когда стоит другая задача, определить все значения, которые может принимать результат вычисления квадратного трёхчлена при различных значениях переменной х, т.е. определить y из выражения y = ax 2 + bx + c, то имеем дело с квадратичной функцией.
При этом корни квадратного уравнения являются нулями квадратичной функции.
Квадратный трёхчлен также можно представить в виде
Это представление удобно использовать при построении графика и изучении свойств квадратичной функции действительного переменного.

Графиком квадратичной функции является парабола, вершина которой находится в точке 
Парабола обладает еще одним интересным свойством, которое также используется как её определение.
Парабола представляет собой множество точек плоскости, расстояние от которых до определенной точки плоскости, называемой фокусом параболы, равно расстоянию до определенной прямой, называемой директрисой параболы.
Построить эскиз графика квадратичной функции можно по характерным точкам.
Например, для функции y = x 2 берем точки
| x | 0 | 1 | 2 | 3 |
| y | 0 | 1 | 4 | 9 |
Соединяя их от руки, строим правую половинку параболы. Левую получаем симметричным отраженим относительно оси ординат.
Для построения эскиза графика квадратичной функции общего вида в качестве характерных точек удобно брать координаты её вершины, нули функции (корни уравнения), если они есть, точку пересечения с осью ординат (при x = 0, y = c) и симметричную ей относительно оси параболы точку (−b/a; c).
| x | −b/2a | x1 | x2 | 0 | −b/a |
| y | −(b 2 − 4ac)/4a | 0 | 0 | с | с |
| при D ≥ 0 | |||||
Производная квадратичной функции вычисляется по формуле (ax 2 + bx + c)’ = 2ax + b.
Формулы для такого перехода можно выучить наизусть, а можно научиться выделять полный квадрат из трёхчлена с заданными коэффициентами. Это умение весьма полезно также для решения некоторых уравнений и неравенств, для вычисления интегралов и т.д.
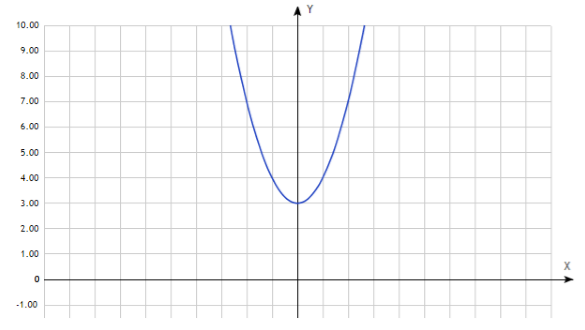
Итак, чтобы построить график функции y = 3x 2 − 5x + 2 из графика y = x 2 нужно последний сдвинуть по оси Ox вправо на 5/6 ≈ 0,83 единицы. Затем растянуть вдоль оси Oy в 3 раза и, наконец, опустить по оси Oy на 1/12 ≈ 0,08 единицы.
Посмотрите, что получилось.
Если Вы являетесь моим учеником или подписчиком, то можете поработать с интерактивными версиями этих графиков.
Преобразуем выражение с выделением полного квадрата: 
Строим график функции 
Видеоуроки с параболой.
Графики квадратичной функции и коэффициенты квадратного трёхчлена.
Положение и вид параболы в зависимости от знака и значения параметра c.
Построение параболы по характерным точкам.
Быстрое построение параболы как графика квадратичной функции.
Другие случаи. Примеры построения.
Задачи на анализ графика квадратичной функции.
Задания вида «Установить соответствие между коэффициентами квадратного трёхчлена и приведенными графиками квадратичной функции» встречаются в ОГЭ по математике в 9-ом классе, а также необходимы сдающим ЕГЭ за 11 класс в качестве промежуточного действия.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено.
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Параграф 2. Повторение и расширение сведений о функции.
Работу выполнил: Косярский А.А. студент группы 45.2
Пункт 2.1. Понятие числовой функции. Простейшие свойства числовых функций.
1. Понятие числовой функции
2. График функции
Графиком функции f называется множество всех точек координатной плоскости
с координатами (x; f (x)), где первая координата x
«пробегает» всю область определения функции, а вторая координата
равна соответствующему значению функции f в точке x
3. Возрастающие и убывающие функции
Функция f(x) возрастающая на множестве P:
если x2 > x1, то f(x2) > f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)
Функция f(x) убывающая на множестве P:
если x2 > x1, то f(x2)
4. Чётные и нечётные функции
Функция f(x) чётная:
если f(-x) = f(x)
для любых x из области определения.
График чётной функции симметричен относительно Oy
Объяснение и обоснование
1. Понятие функции. С понятием функции вы ознакомились в курсе алгебры.
Напомним, что зависимость переменной y от переменной x называется функцией, если
каждому значению x соответствуе единственное значение y.
В курсе алгебры и начал математического анализа мы будем пользоваться
следующим определением числовой функции.
Числовой функцией с областью определения D называется зависимость,
при которой каждому числу x из множества D ставится в соответствие
единственное число y.
Функции обозначают латинскими (иногда греческими) буквами. Рассмотрим
произвольную функцию f. Число y, соответствующее числу x (на рисунке 9 это
показано стрелкой), называют значением функции f в точке x и обозначают f (x).
Чаще всего функцию задают с помощью какой-либо формулы. Если нет
дополнительных ограничений, то областью определения функции, заданной
формулой, считается множество всех значений переменной, при которых эта
формула имеет смысл.
Например, если функция задана формулой y = √x + 1, то её область
определения: x ≥ 0, то есть D(y) = [0;+∞), а область значений:
y ≥ 1, то есть E(y) = [1;+∞).
Функция может задаваться не только при помощи формул, но и сс помощью
таблицы, графика или словесного описания. Например, на рисунке 10
графически задана функция y = f(x) с областью определения
D(f) = [-1;3] и множеством значений E(f) = [1;4]
3. Возрастающие и убывающие функции. Важными характеристиками
функций являются их возрастание и убывание.
На рисунке 15 приведён график ещё одной возрастающей функции
y = x³. Действительно, при x2 > x1 имеем x2³ > x1³,
то есть f(x2) > f(x1).
Функция f(x) называется убывающей на множестве P, если
большему значению аргумента из этого множества соответствует
меньшее значение функции.
То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) x1 имеем
-2⋅
отметим, что для возрастающих и убывающих функций выполняются
свойства, обратные утверждениям, содержащимся в определении.
Например, если x² > 8, то есть x² > 2², то,
учитывая возрастание функции f(x) = x², получаем x > 2.
4. Чётные и нечётные функции. Рассмотрим функции, области
определения которых симметричны относительно начала координат, то
есть содержат вместе с каждым числом x и число (-x). Для таких
функций вводятся понятия чётности и нечётности.
Функция f называется чётной, если для любого x из её области определения
f(-x) = f(x).
Если функция f(x) чётная, то ее графику вместе с каждой точкой
M с координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;f(x)). Точки M и M1
расположены симметрично относительно оси Oy (рис. 18), поэтому
и весь график чётной функции расположен симметрично относительно оси OY.
Если функци f(x) нечётная, то её графику вместе с каждой точкой M с
координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;-f(x)). Точки M и M1
расположены симметрично относительно начала координат (рис. 19), поэтому
и весь график нечётной функции расположен симметрично относительно начала координат.
Например, график нечётной функции y = 1/x (см. пункт 4 табл. 2) симметричен относительно
начала координат, то есть точки O.
ВОПРОСЫ ДЛЯ КОНТРОЛЯ:
ПРИМЕРЫ РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАНИЙ
УПРАЖНЕНИЯ К ПАРАГРАФУ
5. Обоснуйте, что заданная функция является возрастающей (на её области определения):
1) y = 3x 2) y = x + 5 3) y = x³ 4) y = x 5 5) y = √(x)
8. Докажите, что на заданном промежутке функция убывает:
1) y = 3/x, где x 0
9. Докажите, что функция y = x² на промежутке [0; + ∞) возрастает, а на промежутке (- ∞;0] убывает.
11. Используя утверждения, приведённые в примере 6:
1) Обоснуйте, что уравнение x³ + x = 10 имеет единственный корень x = 2;
2) Подберите корень уравнения √(x) + x = 6 и докажите, что других корней это уравнение не имеет.
12. Обоснуйте, что заданная функция является чётной:
1) y = x 6 2) y = 1/x² + 1 3) y = √ (x² + 1) 4) y = √ (|x| + x 4 )




.png)

.png)





















