Функция что это значит
Что такое функция
Понятие функции – одно из основных в математике.
На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.
Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.
1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.
Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.
2. Можно дать и другое определение.
Функция – это определенное действие над переменной.
Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.
3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.
Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.
Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:
Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.
А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:
Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.
Очень сложно было бы описать такое соответствие математически, не правда ли?
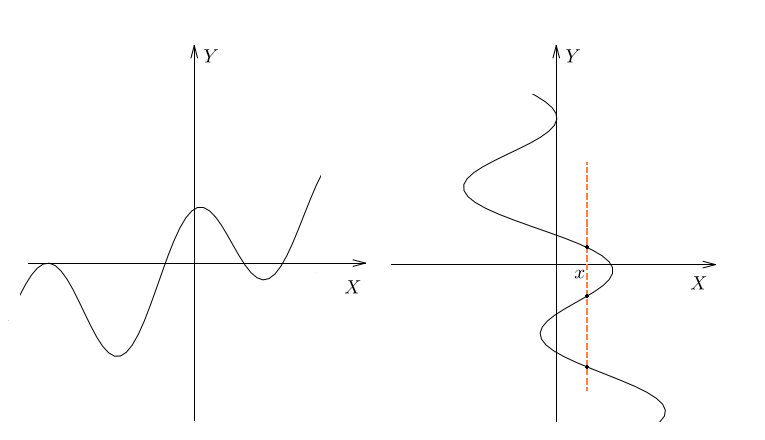
Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?
Ты нашел то, что искал? Поделись с друзьями!
Перечислим способы задания функции.
Это примеры функций, заданных формулами.
К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.
ФУНКЦИЯ
Смотреть что такое «ФУНКЦИЯ» в других словарях:
ФУНКЦИЯ — (лат. functio – исполнение) обязанность, круг деятельности. «Функция – это существование, мыслимое нами в действии» (Гёте). Наука о функциях органов живых существ – физиология; специальная наука о функциях нервной системы – физиология органов… … Философская энциклопедия
функция — Команда или группа людей, а также инструментарий или другие ресурсы, которые они используют для выполнения одного или нескольких процессов или деятельности. Например, служба поддержки пользователей. Этот термин также имеет другое значение:… … Справочник технического переводчика
функция — См … Словарь синонимов
ФУНКЦИЯ — (лат. functio). В физиологии: отправление каким либо органом ему одному свойственных действий, как напр., дыхание, пищеварение. 2) в математике: величина, зависящая от другой переменной величины. Словарь иностранных слов, вошедших в состав… … Словарь иностранных слов русского языка
Функция — [function] 1. Зависимая переменная величина; 2. Соответствие y=f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение… … Экономико-математический словарь
Функция — (от латинского functio исполнение, осуществление), 1) деятельность, обязанность, работа; внешнее проявление свойств какого–либо объекта в данной системе отношений (например, функция органов чувств, функция денег). 2) Функция в социологии роль,… … Иллюстрированный энциклопедический словарь
ФУНКЦИЯ — (от лат. functio исполнение осуществление). 1) деятельность, обязанность, работа; внешнее проявление свойств какого либо объекта в данной системе отношений (напр., функция органов чувств, функция денег)2)] Функция в социологии роль, которую… … Большой Энциклопедический словарь
ФУНКЦИЯ — ФУНКЦИЯ, в математике одно из основных понятий, выражение, определяющее регулярную зависимость между двумя множествами переменных величин, заключающуюся в том, что каждому элементу одного множества соответствует определенная, единственная… … Научно-технический энциклопедический словарь
ФУНКЦИЯ — (function) Взаимосвязь между двумя и более переменными. Если у является функцией от х и записывается в виде y=f(x), то, если значение аргумента х известно, функция позволяет показывает, как найти значение у. Если у – однозначная функция от х, то… … Экономический словарь
ФУНКЦИЯ — (от лат. исполняю, совершаю) центр, понятие в методологии функционального и структурно функционального анализа об в. Понятие “Ф.” стало активно использоваться в социальных науках со вт. пол. 19 в. в связи с проникновением сначала… … Энциклопедия культурологии
Значение слова «функция»
1. Явление, зависящее от другого и изменяющееся по мере изменения другого явления. Литература в целом мире признается как одна из функций общественного бытия. Салтыков-Щедрин, Признаки времени.
2. Мат. Переменная величина, меняющаяся в зависимости от изменения другой величины (аргумента). Тригонометрические функции. □ [Володя], бойко постукивая мелом о черную доску, толкует о функциях, синусах, координатах и т. п. Л. Толстой, Отрочество.
3. Биол. Работа, производимая органом, организмом, как проявление его жизнедеятельности. Вот вам азбука биологии: если какой-нибудь орган продолжительное время не упражнять, то он утрачивает способность отправлять свои функции. Федин, Города и годы. [Котельников:] Проблема сводится к восстановлению жизненных функций организма, пораженного тем или иным ядом. Лавренев, Мы будем жить!
4. перен. Обязанность, круг деятельности. — [Развалихин] утром сказал, что пойдет в школу проводить обществоведение вместо тебя. «Это, говорит, моя прямая функция, а не Корчагина». Н. Островский, Как закалялась сталь.
5. Значение, назначение, роль. Функция творительного падежа. Функции денег.
[От лат. functio — исполнение]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Функция (философия) — обязанность, круг деятельности.
Функция (работа) — работа, производимая органом, организмом, прибором; роль, значение чего-либо; назначение чего-либо.
Функция (литературоведение) — назначение персонажа в литературном произведении.
Социальная функция — использование того или иного механизма социальных взаимодействий для достижения определённой цели или реализации определённых ценностей.
Функция (математика) — закон зависимости одной величины от другой.
Функция (программирование) — вид подпрограммы в информатике.
Функциональная зависимость (программирование) — в теории реляционных баз данных.
ФУ’НКЦИЯ, и, ж. [латин. functio — выполнение работы]. 1. Явление, зависящее от другого и изменяющееся по мере изменения этого другого явления (книжн.). 2. Переменная величина, меняющаяся в зависимости от изменения другой величины (мат.). Величина давления газа есть функция величины его объема. 3. Работа, производимая органом, организмом (биол., физиол.). Отделение слюны является основной функцией слюнной железы. 4. перен. Обязанность, круг деятельности чего-н., подлежащая исполнению работа (книжн.). Служебные функции. Исполнять свою функцию в обществе. Функции государственного управления. 5. Значение, назначение, роль (книжн.). Ф. математического знака. Ф. родительного падежа.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
фу́нкция
1. перен. книжн. обязанность, круг деятельности чего-либо, подлежащая исполнению работа ◆ Служебные функции. ◆ Исполнять свою функцию в обществе. ◆ Функции государственного управления.
2. книжн. значение, назначение, роль ◆ Функция математического знака. ◆ Функция родительного падежа.
3. матем. переменная величина, меняющаяся в зависимости от изменения другой величины, а также закон, определяющий свойства такого изменения ◆ Величина давления газа есть функция величины его объёма.
4. книжн. явление, зависящее от другого и изменяющееся по мере изменения этого другого явления
5. биол. физиол. работа, производимая органом, организмом. ◆ Выделение слюны является основной функцией слюнной железы.
7. комп. в программировании — фрагмент программного кода (подпрограмма), к которому можно обратиться из другого места программы.
Что такое Функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.