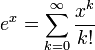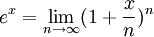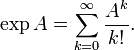Функция exp что значит

Экспоненциальная функция

Содержание

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:

Свойства

Экспонента от комплексного аргумента

От комплексного аргумента z = x + iy экспонента определяется следующим образом:

Вариации и обобщения

Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

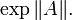
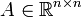
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение 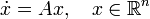с начальным условием x(0) = x₀ имеет своим решением x(t) = exp(At)x₀.

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x) :

См. также

Полезное

Смотреть что такое «Экспоненциальная функция» в других словарях:

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Большой Энциклопедический словарь

экспоненциальная функция — экспонента — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы экспонента EN exponential function … Справочник технического переводчика

экспоненциальная функция — то же, что показательная функция. * * * ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ, то же, что показательная функция (см. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ) … Энциклопедический словарь

экспоненциальная функция — eksponentinė funkcija statusas T sritis fizika atitikmenys: angl. exponential function vok. exponentielle Funktion, f rus. экспоненциальная функция, f pranc. fonction exponentielle, f … Fizikos terminų žodynas

Экспоненциальная функция — функция у = ex, то есть Показательная функция. Обозначается также y = exp х. Иногда Э. ф. называют и функцию у = ax при любом основании а > 0 … Большая советская энциклопедия

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — показа тельная функция, функция у=е х;обозначается также y = ехр х. Иногда Э. ф. наз. и функцию у = а х при любом основании а>0. БСЭ 3 … Математическая энциклопедия

ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Естествознание. Энциклопедический словарь

экспоненциальная — функция [ Словарь иностранных слов русского языка

Источник

Экспонента в математике – это функция «y=ex», которая отражает непрерывный рост с коэффициентом. В этой функции «е»‎ ‎– это число Эйлера, которое представляет собой постоянную (

2,72). Говоря иначе, рост любой величины прямо пропорционален ее значению.

Допустим, мы слепили снежный ком и спустили его с горы. Он начинает катиться, одновременно наращивая объем. При этом чем больше он становится, тем выше скорость его движения. И наоборот: чем быстрее он катится, тем быстрее увеличивается в размерах. Получается, что масса и скорость снежного кома (y) экспоненциально возрастают со временем (x).

Экспонента в жизни. Экспоненциальный рост

Рассмотрим примеры экспоненты и экспоненциального роста в реальной жизни.

Вклад в банке под процент. У всех процессов, идущих по экспоненте, есть одна особенность: за одно и то же количество времени их параметры меняются одинаковое количество раз.

Например, вклад в банке каждый год увеличивается на определенное количество процентов. Если положить 1000 рублей в банк под 10% годовых, то через год вклад будет составлять 1100 рублей. А в следующем году 10% будут начисляться уже исходя из суммы в 1100 рублей. То есть, вклад вырастет сильнее, и так размер прироста будет увеличиваться из года в год.

Численность животных. Чем больше популяция животных, тем больше они размножаются. Соответственно, рост численности популяции прямо пропорционален количеству особей в ней.

Чем экспоненциальный рост отличается от линейного?

Линейный рост характеризуется стабильным прибавлением постоянной, а экспоненциальный рост – это следствие многократного умножения на постоянную. То есть если линейный рост на графике представляет собой стабильную линию, то экспоненциальный рост характеризуется быстрым взлетом.

В качестве примера можно привести обычную ходьбу. Если длина одного шага составляет 1 метр, то через 6 шагов человек преодолевает расстояние в 6 метров. Это и называется линейным ростом.

При экспоненциальном росте длина каждого шага в нашем примере увеличивается в 2 раза. То есть сначала человек шагает на 1 метр, потом на 2 метра, потом на 4 метра и так далее. В таком случае за 6 шагов можно пройти 32 метра, что гораздо больше, чем в предыдущем примере.

Источник

Что такое Экспонента

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

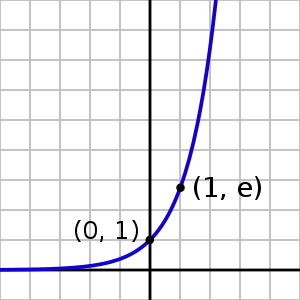
График экспоненты выглядит следующим образом:

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Источник

Примеры работы функции EXP для возведения числа Эйлера в Excel

Функция EXP в Excel используется для возведения числа Эйлера (константа e, которая примерно равна 2,718) в указанную степень и возвращает соответствующее числовое значение.

Примеры использования функции EXP в Excel

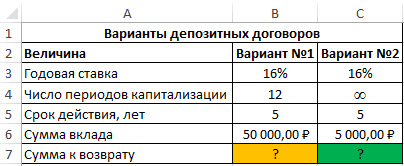
Пример 1. Вкладчику банка предложили два варианта вклада:

Какое предложение является более выгодным? Сумма вклада – 50000 рублей, срок действия договора – 5 лет.

Вид исходной таблицы данных:

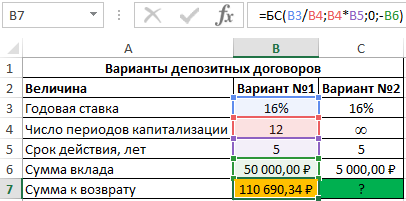
Формула для расчета будущей стоимости вклада для первого варианта депозитного договора:

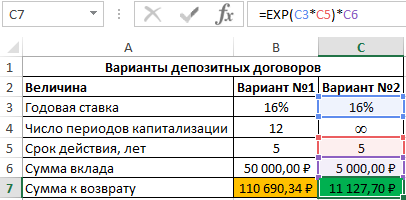
Во втором случае капитализация происходит непрерывно, поэтому можно воспользоваться следующей функцией:

Вариант с непрерывным ростом капитализации является более выгодным.

Расчет скорости деления клеток ткани в Excel

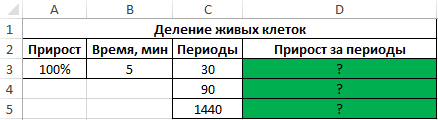
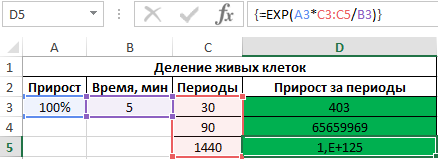
Пример 2. В начальный момент времени была только одна клетка живой материи. Каждые 5 минут такая клетка делится на 2 идентичные клетки. Определить, сколько клеток ткани образуется за 0,5 часа, 1,5 часа, сутки?

Исходная таблица имеет следующий вид:

Для расчета используем формулу массива:

Скорость уменьшения массы радиоактивного вещества с течением времени

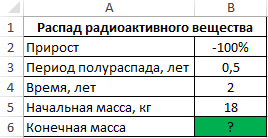
Пример 3. Количество радиоактивного вещества уменьшается вдвое за полгода. Сколько будет весить вещество спустя 2 года, если начальная масса составляла 18 кг.

Вид исходной таблицы:

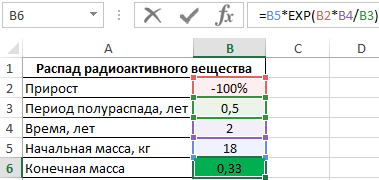
Формула для расчета:

Спустя 2 года от 18 кг останется всего примерно 330 г.

Особенности использования функции EXP в Excel

Функция EXP имеет следующую синтаксическую запись:

Источник

Функция EXP (экспонента) в Microsoft Excel

Функция EXP (экспонента) в Microsoft Excel

Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.

Вычисление экспоненты в Эксель

Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:

где e – это число Эйлера, а n – степень возведения.

Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.

Способ 1: вычисление экспоненты при помощи ручного ввода функции

Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:

То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.

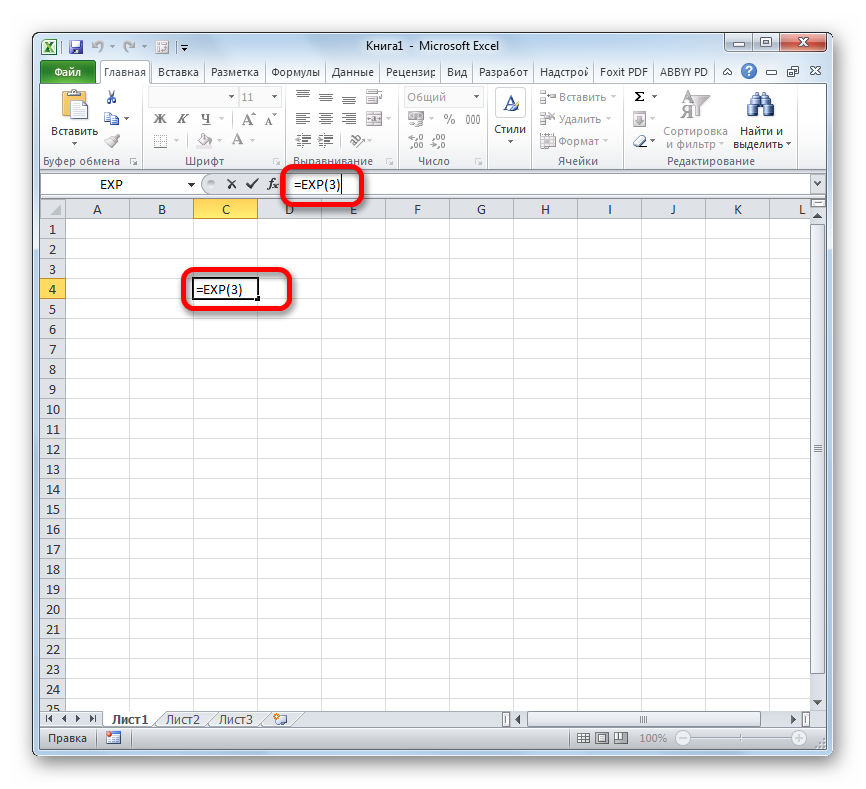
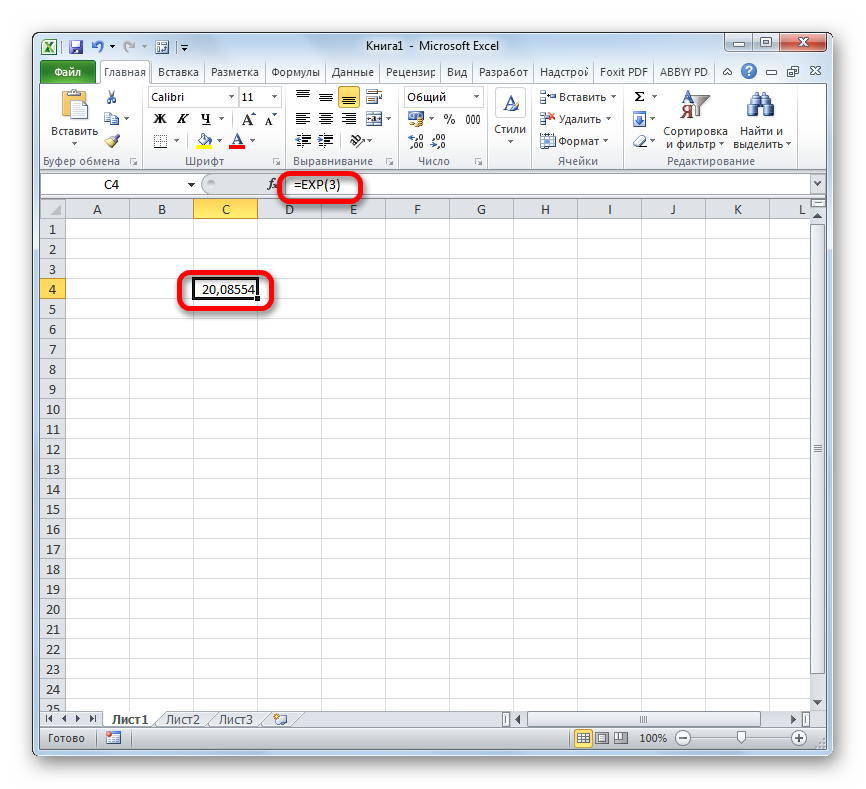
Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:

Способ 2: использование Мастера функций

Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.

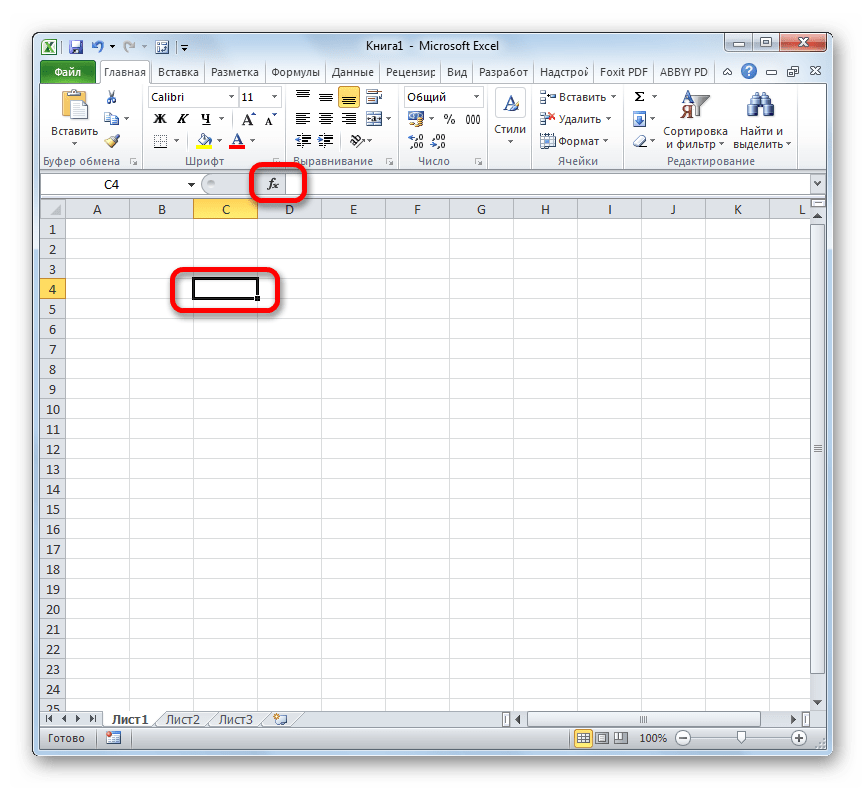
Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.

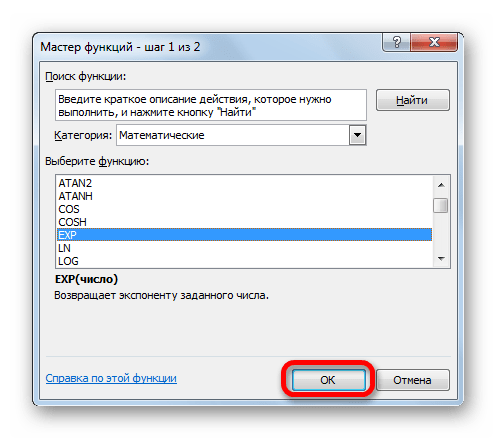
Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».

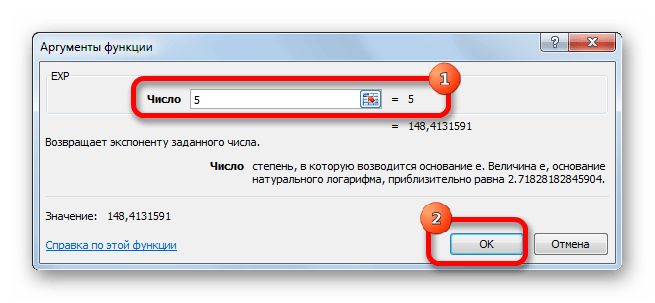
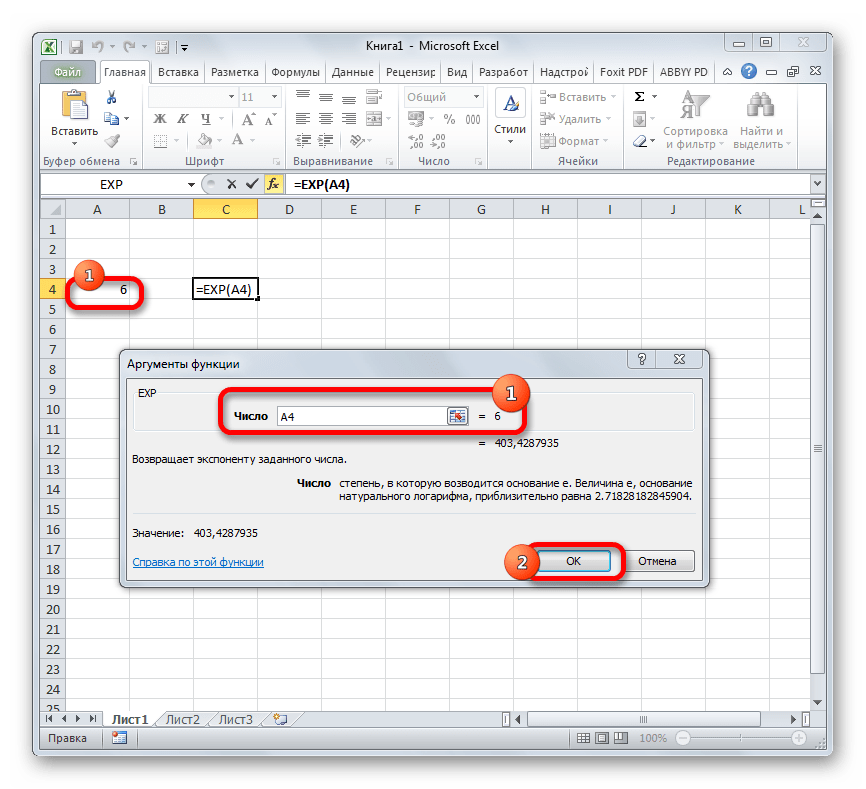
Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».

Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».

Способ 3: построение графика

Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.

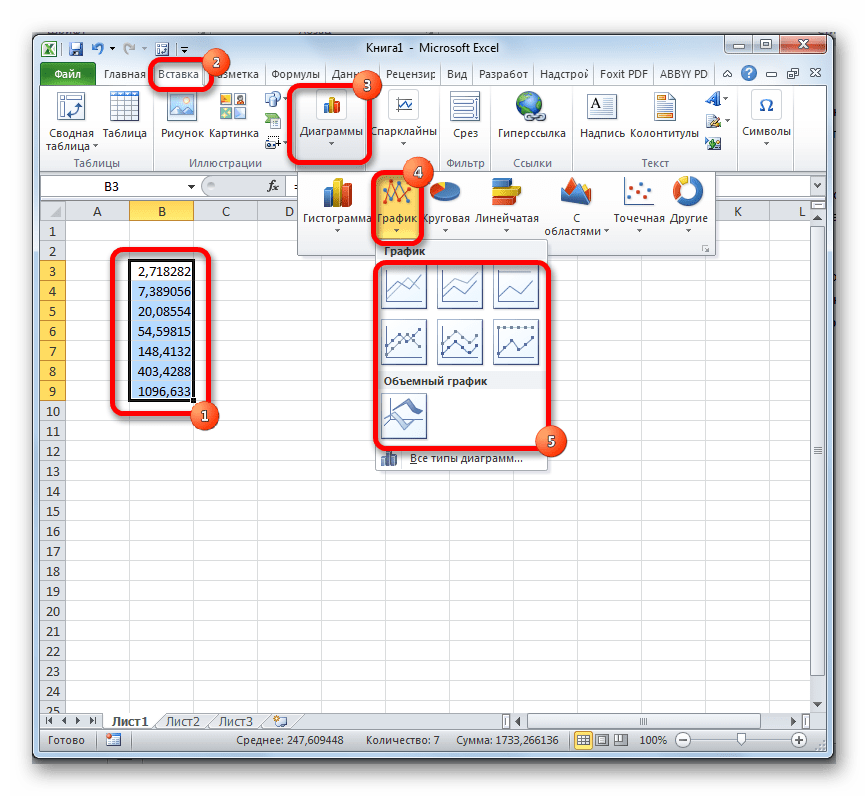
Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.

Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Excel works!

Excel работает за вас

Excel works!

Thanks for Visiting

Экспонента в Excel. Что такое экспонента и как применять?

Экспонента. Что это такое?

Мы знаем, что наш мир описан точными науками — т.е. набором правил и законов более-менее точно описывающих происходящее. Для этого в большинстве случаев помогают функции/формулы. В природе довольно часто встречаются экспоненциальные явления (описываем экспонентой) формулой с числом e, а у = e в степени x уже будет экспоненциальной функцией:

Число e — это т.н. число Эйлера, приблизительно равное 2,72. Примечательно оно тем, что производная от этой функции равна самой функции exp(x)` = exp(x).

Что это вообще такое, и что для нас означает?

Лучше всего, действие экспоненты показывают графики ниже:

Если грубо, то в природе, это действительно встречается часто — чем больше клеток делятся, тем быстрее их становиться больше. Чем больше у вас денег в банке, тем большую прибыль они приносят. Например:

Вы вложили 1 000 руб. в банк, через год они принесли свои 100 руб. процентами, еще через год на вас работают уже 2 работника 1 000 руб. и 100 руб. и так далее пока вы не заберете деньги или не случится банковский кризис.

Кстати население на планете Земля тоже растет по экспоненте;)

Принцип Парето и экспонента

Слышали о таком принципе? Думаю да. «20% усилий приносят 80% результата». Это он. Лучшее определение для запоминания, мне кажется:

20% любителей пива употребляют 80% всего пива

На принципе Парето построен и ABC анализ запасов, например.

Этот принцип Парето — еще один пример экспоненты.

Кстати очень справедливый закон в реальной жизни, подтверждаю своим опытом.Когда-то на первом своем проекте я заметил, что примерно за 20% времени ты создаешь 80% продукта (в количественном эквиваленте), далее работаешь на качество. Т.е. еще 80% времени допиливаешь, ищешь ошибки, настраиваешь. Я даже слышал, что говорят «разработка в стадии экспоненты» — т.е. в стадии приближения к идеалу.

При таком «допиливании» проекта важно вовремя остановиться, ведь продукт никогда не будет идеальным. Поэтому заранее определитесь какое качество вы хотели бы получить в конце. Если делаете не себе, обязательно соберите требования с заказчика. Принцип выглядит примерно так:

Экспонента в Excel

Когда по смыслу функции более-менее объяснил, напишу как считать ее и есть ли функция экспонента в Excel. Само собой есть.

В Эксель все посчитать несложно:

или можно число возвести в степень

Дополнение. Как запомнить 15 знаков числа е?

В качестве отвлечения привожу способ, как запомнить число e c точностью до 15 знаков

Примеры работы функции EXP для возведения числа Эйлера в Excel

Функция EXP в Excel используется для возведения числа Эйлера (константа e, которая примерно равна 2,718) в указанную степень и возвращает соответствующее числовое значение.

Примеры использования функции EXP в Excel

Пример 1. Вкладчику банка предложили два варианта вклада:

Какое предложение является более выгодным? Сумма вклада – 50000 рублей, срок действия договора – 5 лет.

Вид исходной таблицы данных:

Формула для расчета будущей стоимости вклада для первого варианта депозитного договора:

Во втором случае капитализация происходит непрерывно, поэтому можно воспользоваться следующей функцией:

Вариант с непрерывным ростом капитализации является более выгодным.

Расчет скорости деления клеток ткани в Excel

Пример 2. В начальный момент времени была только одна клетка живой материи. Каждые 5 минут такая клетка делится на 2 идентичные клетки. Определить, сколько клеток ткани образуется за 0,5 часа, 1,5 часа, сутки?

Исходная таблица имеет следующий вид:

Для расчета используем формулу массива:

Скорость уменьшения массы радиоактивного вещества с течением времени

Пример 3. Количество радиоактивного вещества уменьшается вдвое за полгода. Сколько будет весить вещество спустя 2 года, если начальная масса составляла 18 кг.

Вид исходной таблицы:

Формула для расчета:

Спустя 2 года от 18 кг останется всего примерно 330 г.

Особенности использования функции EXP в Excel

Функция EXP имеет следующую синтаксическую запись:

МНК: Экспоненциальная зависимость в MS EXCEL

Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.

Метод наименьших квадратов (англ. Ordinary Least Squares, OLS) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК – МНК: Метод Наименьших Квадратов в MS EXCEL.

В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:

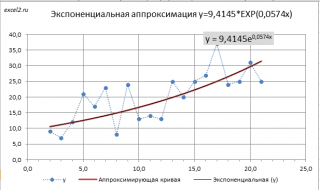
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).

Примечание: Построить линию тренда по методу наименьших квадратов можно также с помощью инструмента диаграммы Линия тренда (Экспоненциальная линия тренда). Поставив в диалоговом окне галочку в поле «показывать уравнение на диаграмме» можно убедиться, что найденные выше параметры совпадают со значениями на диаграмме. Подробнее о диаграммах см. статью Основы построения диаграмм в MS EXCEL.

Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больших по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.

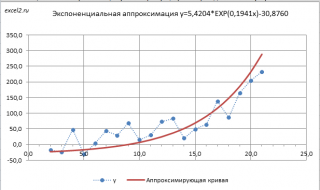
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y, ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).

Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a файл примера лист Экспонента3 ).

Функция РОСТ()

Синтаксис функции следующий:

РОСТ(известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст])

Для работы функции нужно просто ввести ссылки на массив значений переменной Y (аргумент известные_значения_y) и на массив значений переменной Х (аргумент известные_значения_x). Функция рассчитает прогнозные значения Y для Х, указанных в аргументе новые_значения_x. Если требуется, чтобы экспоненциальная кривая y=a*EXP(b*x) имела a=1, т.е. проходила бы через точку (0;1), то необязательный аргумент конст должен быть установлен равным ЛОЖЬ (или 0).

Если среди значений y есть отрицательные, то с помощью функции РОСТ() аппроксимирующую кривую построить не удастся.

Безусловно, использование функции РОСТ() часто удобно, т.к. не требуется делать замену переменных и сводить задачу к линейному случаю.

Наконец, покажем как с помощью функции РОСТ() вычислить коэффициенты уравнения y=a*EXP(b*x).

Чтобы вычислить коэффициент b используйте формулу:

= LN(РОСТ(C26:C45;B26:B45;МИН(B26:B45))/
РОСТ(C26:C45;B26:B45;МАКС(B26:B45)))/
(МИН(B26:B45)-МАКС(B26:B45))

Функция ЛГРФПРИБЛ()

Функция ЛГРФПРИБЛ() на основе имеющихся значений переменных Х и Y подбирает методом наименьших квадратов коэффициенты а и m уравнения y=a*m^x.

Используя свойство степеней a mn =(a m ) n приведем уравнение экспоненциального тренда y=a*EXP(b*x)=a*e b *x = a*(e b ) x к виду y=a*m^x, сделав замену переменной m= e b =EXP(b).

Чтобы вычислить коэффициенты уравнения y=a*EXP(b*x) используйте следующие формулы:

= LN(ЛГРФПРИБЛ(C26:C45;B26:B45)) – коэффициент b

= ИНДЕКС(ЛГРФПРИБЛ(C26:C45;B26:B45);;2) – коэффициент a

Примечание: Особой нужды в функции ЛГРФПРИБЛ() нет, т.к. с помощью логарифмирования и замены переменной показательную функцию y=a*m^x можно свести к линейной ln(y)=ln(a)+x*ln(m)=> Y=A+bx. То же справедливо и для экспоненциальной функции y=a*EXP(b*x).

Источник