Хопфилд что сделал и когда

НациональностьАмериканецАльма-матерSwarthmore College
Корнелл УниверситетИзвестенСеть Хопфилда
Поляритон
Кинетическая корректураНаградыПремия Гарольда Пендера (2002)
Медаль Дирака из ICTP (2002)
Приз Оливера Бакли из Американское физическое общество
Мировая премия имени Альберта Эйнштейна в области науки (2005)
Медаль Бенджамина Франклина (2019)Научная карьераПоляФизика, Молекулярная биология, НеврологияУчрежденияBell Labs
Университет Принстона
Калифорнийский университет в Беркли
Калифорнийский технологический институтТезисКвантово-механическая теория вклада экситонов в комплексную диэлектрическую проницаемость кристаллов (1958)ДокторантАльберт ОверхаузерДокторантыДэвид Дж. С. Маккей
Терри Сейновски
Бертран Гальперин
Стивен Гирвин
Эрик Винфри
Дэвид Бератан
Хосе Онучич
Ли Чжаопин
Санджой Махаджан
Сэм Роуис
Карлос Броуди
Олли Даунс
Гейл Виттенберг

Джон Джозеф Хопфилд (родился 15 июля 1933 г.) Американец ученый, наиболее широко известный своим изобретением ассоциативный нейронная сеть в 1982 году. Сейчас он более известен как Сеть Хопфилда.

Содержание

биография

Хопфилд родился в 1933 году в семье польского физика. Джон Джозеф Хопфилд и физик Хелен Хопфилд. Хелен была второй женой старшего Хопфилда. Он шестой из детей Хопфилда, у него трое детей и шесть внуков.

Он получил свой А.Б. от Swarthmore College в 1954 г. и докторскую степень по физике от Корнелл Университет в 1958 г. (под руководством Альберт Оверхаузер). Два года он проработал в теоретической группе в Bell Laboratories, а впоследствии был преподавателем в Калифорнийский университет в Беркли (физика), Университет Принстона (физика), Калифорнийский технологический институт (Химия и биология) и снова в Принстоне, где он является почетным профессором молекулярной биологии Говарда А. В течение 35 лет он также поддерживал тесные связи с Bell Laboratories.

В 1986 году он был соучредителем Вычислительные и нейронные системы Программа PhD в Калтехе.

Его самые влиятельные работы были «Вклад экситонов в комплексную диэлектрическую проницаемость кристаллов» (1958), в которых описывался поляритон; «Электронный перенос между биологическими молекулами посредством термически активированного туннелирования» (1974), описывающий квантовую механику переноса электронов на большие расстояния; «Кинетическая корректура: новый механизм для уменьшения количества ошибок в биосинтетических процессах, требующих высокой специфичности »(1974);« Нейронные сети и физические системы с возникающими коллективными вычислительными способностями »(1982) (известная как сеть Хопфилда) и, с DW Tank,« Нейронные вычисления решения в задачах оптимизации »(1985). Его текущие исследования и недавние статьи в основном сосредоточены на том, как потенциал действия время и синхронность могут использоваться в нейробиологических вычислениях.

Награды и почести

Он был награжден Медаль Дирака МЦТФ в 2002 году за его междисциплинарный вклад в понимание биологии как физического процесса, включая процесс корректуры в биомолекулярном синтезе и описание коллективная динамика и вычисления с аттракторами в нейронных сетях, а Приз Оливера Бакли Американского физического общества за работу по взаимодействию между светом и твердые тела. Хопфилд был избран членом Национальная Академия Наук в 1973 г. член Американская академия искусств и наук в 1975 г. и член Американское философское общество в 1988 г. [1] [2] [3] В 1985 году Хопфилд получил премию Golden Plate Award Американская академия достижений. [4] Он получил Мировая премия имени Альберта Эйнштейна в области науки в 2005 году. [5] В 2006 году он был президентом Американского физического общества. [6]

Источник

Нейронная сеть Хопфилда на пальцах

Статья посвящена введению в нейронные сети и примеру их реализации. В первой части дано небольшое теоретическое введение в нейронные сети на примере нейронной сети Хопфилда. Показано, как осуществляется обучение сети и как описывается ее динамика. Во второй части показано, как можно реализовать алгоритмы, описанные в первой части при помощи языка С++. Разработанная программа наглядно показывает способность нейронной сети очищать от шума ключевой образ. В конце статьи есть ссылка на исходный код проекта.

Теоретическое описание

Введение

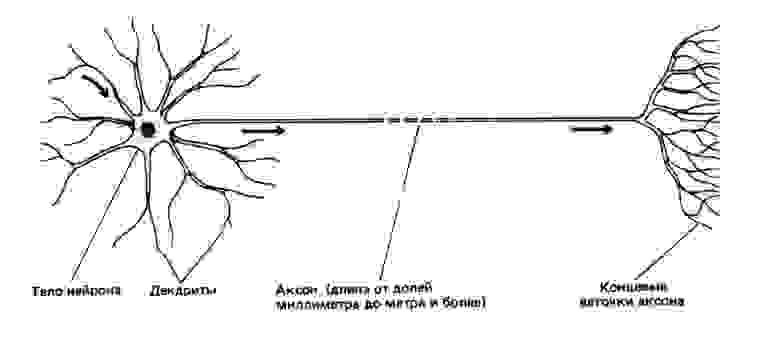
Для начала, необходимо определить, что такое нейрон. В биологии нейрон — специализированная клетка, из которой состоит нервная система. Биологический нейрон имеет строение, показанное на рис.1.

Рис.1 Схема нейрона

Нейронную сеть можно ввести как совокупность нейронов и их взаимосвязей. Следовательно, для того, чтобы определить искусственную (не биологическую) нейронную сеть необходимо:

В качестве архитектуры нейронной сети будет использоваться сеть Хопфилда. Данная модель, видимо, является наиболее распространенной математической моделью в нейронауке. Это обусловлено ее простотой и наглядность. Сеть Хопфилда показывает, каким образом может быть организована память в сети из элементов, которые не являются очень надежными. Экспериментальные данные показывают, что при увеличении количества вышедших из строя нейронов до 50%, вероятность правильного ответа крайне близка к 100%. Даже поверхностное сопоставление нейронной сети (например, мозга) и Фон-Неймановской ЭВМ показывает, насколько сильно различаются эти объекты: к примеру, частота изменения состояний нейронов («тактовая частота») не превышает 200Гц, тогда как частота изменения состояния элементов современного процессора может достигать нескольких ГГц (Гц).
Формальное описание сети Хопфилда

Сеть состоит из N искусственных нейронов, аксон каждого нейрона связан с дендритами остальных нейронов, образуя обратную связь. Архитектура сети изображена на рис. 2.

Рис.2 Архитектура нейронной сети Хопфилда

Каждый нейрон может находиться в одном из 2-х состояний:

где — состояние нейрона в момент . «Возбуждению» нейрона соответствует , а «торможению» . Дискретность состояний нейрона отражает нелинейный, пороговый характер его функционирования и известный в нейрофизиологи как принцип «все или ничего».

Динамика состояния во времени -ого нейрона в сети из нейронов описывается дискретной динамической системой:

где — матрица весовых коэффициентов, описывающих взаимодействие дендритов -ого нейрона с аксонами -ого нейрона.

Стоит отметить, что и случай не рассматриваются.

Обучение и устойчивость к шуму

Обучение сети Хопфилда выходным образам сводится к вычислению значений элементов матрицы . Формально можно описать процесс обучения следующим образом: пусть необходимо обучить нейронную сеть распознавать образов, обозначенных . Входной образ представляет собой: где — шум, наложенный на исходный образ .
Фактически, обучение нейронной сети — определение нормы в пространстве образов . Тогда, очистка входного образа от шума можно описать как минимизацию этого выражения.

Важной характеристикой нейронной сети является отношение числа ключевых образов , которые могут быть запомнены, к числу нейронов сети : . Для сети Хопфилда значение не больше 0.14.

Вычисление квадратной матрицы размера для ключевых образов производится по правилу Хебба:

где означает -ый элемент образа .

Стоит отметить, что в силу коммутативности операции умножения, соблюдается равенство

Входной образ, который предъявляется для распознавания соответствует начальным данным для системы, служащий начальным условием для динамической системы (2):

Уравнений (1), (2), (3), (4) достаточно для определения искусственной нейронной сети Хопфилда и можно перейти к ее реализации.

Реализация нейронной сети Хопфилда

Реализация нейронной сети Хопфилда, определенной выше будет производиться на языке C++. Для упрощения экспериментов, добавим основные определения типов, напрямую связанных с видом нейрона и его передаточной функции в класс simple_neuron, а производные определим далее.

Самыми основными типами, напрямую связанными с нейроном являются:

На основе этих типов можно ввести остальные базовые типы:

Обучение сети, или, вычисление элементов матрицы в соответствии с (3) производится функцией learn_neuro_net, принимающей на вход список обучающих образов и возвращающей объект типа link_coeffs_t. Значения вычисляются только для нижнетреугольных элементов. Значения верхнетреугольных элементов вычисляются в соответствии с (4). Общий вид метода learn_neuro_net показан в листинге 2.

Обновление состояний нейронов реализовано с помощью функтора neuro_net_system. Аргументом метода _do функтора является начальное состояние , являющееся распознаваемых образом (в соответствии с (5)) — ссылка на объект типа neurons_line.

Метод функтора модифицирует передаваемый объект типа neurons_line до состояния нейронной сети в момент времени . Значение жестко не фиксировано и определяется выражением:

т.е., когда состояние каждого нейрона не изменилось за 1 «такт».

Для вычисления (2) применены 2 алгоритма STL:

Исходный код функтора neurons_net_system и метода calculate класса simple_neuron показан в листинге 3.

Для вывода в консоль входных и выходных образов создан тип neurons_line_print_descriptor, который хранит ссылку на образ и формат форматирования (ширину и высоту прямоугольника, в который будет вписан образ). Для этого типа переопределен оператор Листинг 4. Вывод в поток состояния нейронной сети

Пример работы нейронной сети

Для проверки работоспособности реализации, нейронная сеть была обучена 2 ключевым образам:

Рис.3 Ключевые образы

На вход подавались искаженные образы. Нейронная сеть корректно распознала исходные образы. Искаженные образы и распознанные образы показаны на рис.4, 5

Рис.4 Распознавание образа 1

Рис.5 Распознавание образа 2

Запуск программы производится из командной строки строчкой вида: AppName WIDTH HEIGHT SOURCE_FILE [LEARNE_FILE_N], где:

В репозитории проект CMake, из которого можно сгенерировать проект Visual Studio (VS2015 компилирует проект успешно) или обычные Unix Makefile’ы.

Источник

Русские Блоги

Нейронная сеть Хопфилда и ее реализация на Python (1)

Резюме

Хопфилд сыграл ключевую роль в возрождении исследований нейронных сетей в начале 1980-х годов. В начале своей академической деятельности Хопфилд изучал взаимодействие между светом и твердыми телами, а затем сосредоточился на механизме переноса электронов между биомолекулами, своих академических исследованиях в области математики и физики и своем более позднем опыте в биологии. Комбинация, в настоящее время называется междисциплинарной, и она заложила прочную основу для исследования нейронных сетей и концепции в будущем. В 1982 году была предложена нейронная сеть Хопфилда, которая может решать большой класс задач распознавания образов, а также может дать приближенное решение класса задач комбинаторной оптимизации. Эта модель нейронной сети позже была названа нейронной сетью Хопфилда. В 1985 году Хопфилд опубликовал в PRD статью, в которой подробно описал взаимосвязь между сетью и моделью Изинга и предложил ее характеристики фазового перехода.
Эта статья в основном раскрывает понимание и опыт автора нейронной сети Хопфилда в последние дни с четырех аспектов, в основном на основе ее реализации на Python, на основе оптимизации кода и оптимизации результатов. Основные приложения и возможные улучшения. И уточнить его связь с моделью Изинга и характеристиками фазового перехода. Поскольку последняя часть включает в себя много знаний, связанных с термодинамикой, знания бакалавриата немного застенчивы, поэтому я в основном привожу некоторый опыт автора и смутные чувства.

основное содержание

1. Сетевые характеристики

В предыдущем исследовании мы познакомились со многими распространенными нейронными сетями. Например, выходной сигнал нейрона может напрямую воздействовать на свою собственную RNN в следующий период времени. FNN разработана и применяется в наибольшей степени. Из-за присущих локальным узорам изображения (например, глаз, носа, рта и т. Д. На лице), Следовательно, обработка изображения и божественная сеть объединяются, чтобы привести к CNN сверточной нейронной сети.Чтобы преодолеть исчезновение градиента, передаточные функции, такие как ReLU и maxout, заменяют сигмовидную DNN. Как нейронные сети, с которыми мы очень хорошо знакомы, эти сети были очень зрелыми в отрасли и в жизни и получили широкое распространение. Нейронная сеть Хопфилда является очень типичной нейронной сетью с обратной связью.В дополнение к прямой связи между теми же нейронами, что и нейронная система с прямой связью, очевидно, что существует еще и обратная связь. В целом структуру сети Хопфилда можно описать следующей схематической диаграммой:

Как видно из принципиальной схемы, структура нейронной сети имеет следующие три характеристики:

Второй, подробный алгоритм

Три, программа Python подробно

Прежде всего, объясните имя библиотеки, тип библиотеки и модуль, который вы используете. Основные из них, используемые в этом коде, следующие:

После этого я начал разбивать алгоритм на понятные блоки в соответствии со своими привычками. В этом процессе обнаруживается, что существует множество шагов, на которых необходимо преобразовать изображение в двоичную матрицу или ее обратную операцию, поэтому сначала удобно написать несколько функций.
Следующая функция используется для преобразования изображений в формате jpg или jpeg в двоичную матрицу. Сначала сгенерируйте нулевую матрицу x, чтобы классифицировать значения цветности в imgArray, чтобы получить окончательную двоичную матрицу. Эта функция будет вызываться несколько раз по всему тексту.

Ниже приводится определение его обратного преобразования.Поскольку функция для этого обратного преобразования уже существует в Python, ее можно использовать с небольшой обработкой.

На этом этапе вы можете ввести исходное изображение, чтобы получить двоичную матрицу. Здесь следует отметить, что при выборе изображения старайтесь выбирать черно-белое изображение, чтобы получить хорошее отображение. Вы можете настроить размер и порог, чтобы изменить контраст и размер окончательного изображения. Следующий рисунок является выходом:

Ниже приводится еще одна программа, написанная для удобства вычислений, с использованием x.shape для получения номера каждого измерения матрицы x, тем самым получая вектор с нулевыми значениями из m элементов. Присвойте x вектору tmp1 в порядке i \ j. Наконец, вектор, преобразованный из матрицы, получен.

Чтобы лучше увидеть влияние итерации на систему, мы вычисляем энергию системы после каждой итерации в соответствии с определением и, наконец, рисуем изображение E для проверки предыдущей точки.

После определения основной функции мы переходим к основной части и вызываем функцию, определенную выше, чтобы кратко выразить основную функцию. Вы можете настроить размер и порог, чтобы получить лучшие входные эффекты, но это также может увеличить объем компьютерных вычислений и увеличить время работы. Чтобы повысить способность к обобщению, мы открываем обучающую картинку после регуляризации и получаем матрицу весов с помощью этой программы.

Первым шагом после получения весовой матрицы, естественно, является ввод тестового изображения.После регуляризации тестовое изображение преобразуется в двоичное изображение в соответствии с методом изображение-матрица-изображение, как показано на рисунке ниже.

На последнем шаге мы используем матрицу тестового изображения (матрицу состояний нейрона) для итеративного обновления, пока не будет достигнуто определенное количество итераций. Наконец, матрица в конце итерации преобразуется в двоичное изображение для вывода. Используя ранее определенную функцию, можно сказать, что этот шаг выполняется за один раз.

На этом программа Python для реализации Hopfiled завершена. Давайте посмотрим на предыдущую входную картинку Хиллари, какой вывод мы можем получить после обучения-повторного вызова?

После ввода тестового изображения и повторения 8000 раз программа может более точно вспомнить исходное изображение Хиллари. И видно, что энергия системы соответствует характеристикам уменьшения с количеством итераций и постепенно переходит в стационарное или метастабильное состояние. У программы еще много недостатков, например, слишком долго запускается в случае высокой точности фотографии (в основном расчет функции энергии).
В этой статье автор в основном представляет основные характеристики дискретных нейронных сетей Хопфилда, алгоритмы и реализацию программ Python, а также некоторые недавние мысли и опыт. В следующей статье я в основном объясню его термодинамические характеристики.Для нейронных сетей решение модели Изинга может получить многие термодинамические характеристики и объяснить некоторые интуитивные явления, поэтому это также очень важно. Быть в курсе!

Источник

Хопфилд, Джон

физика, молекулярная биология, нейробиология

Терри Сейновски, Дэвид Маккей

Джон Джозеф Хопфилд (англ. John Joseph Hopfield ; род. 15 июля 1933 года) — американский учёный в основном известный за изобретение ассоциативной нейронной сети в 1982 году. Эта сеть известна под названием сети Хопфилда.

Получил докторскую степень по физике в Корнелльском университете в 1958 году. В течение двух лет проработал в теоретической группе Bell Laboratories, а затем работал на факультетах Калифорнийского университета в Беркли, Принстонского университета и Калифорнийского технологического института.

В 2001 году он был награжден медалью Дирака за вклад в развитие понимания биологии как физического процесса. В 2006 году он был президентом Американского физического общества.

Основные публикации

Ссылки

Полезное

Смотреть что такое «Хопфилд, Джон» в других словарях:

Медаль Дирака — (официально: англ. Dirac Medal of the Abdus Salam International Centre for Theoretical Physics медаль Дирака от Международного центра теоретической физики имени Абдуса Салама) медаль (а также премия) в области физики, ежегодно присуждаемая… … Википедия

Искусственная нейронная сеть — У этого термина существуют и другие значения, см. Нейронная сеть (значения). Схема простой нейросети. Зелёным цветом обозначены входные нейроны, голубым скрытые нейроны, жёлтым выходной нейрон … Википедия

Рекуррентная нейронная сеть — Для улучшения этой статьи желательно?: Добавить иллюстрации. Рекуррентные нейронные сети (англ. … Википедия

Искусственная нейросеть — Запрос «Нейронная сеть» перенаправляется сюда. Cм. также другие значения. Схема простой нейросети. Зелёным обозначены входные элементы, жёлтым выходной элемент Искусственные нейронные сети (ИНС) математические модели, а также их программные или… … Википедия

Нейронные сети — Запрос «Нейронная сеть» перенаправляется сюда. Cм. также другие значения. Схема простой нейросети. Зелёным обозначены входные элементы, жёлтым выходной элемент Искусственные нейронные сети (ИНС) математические модели, а также их программные или… … Википедия

Нейросети — Запрос «Нейронная сеть» перенаправляется сюда. Cм. также другие значения. Схема простой нейросети. Зелёным обозначены входные элементы, жёлтым выходной элемент Искусственные нейронные сети (ИНС) математические модели, а также их программные или… … Википедия

Нейросеть — Запрос «Нейронная сеть» перенаправляется сюда. Cм. также другие значения. Схема простой нейросети. Зелёным обозначены входные элементы, жёлтым выходной элемент Искусственные нейронные сети (ИНС) математические модели, а также их программные или… … Википедия

Рекуррентные нейронные сети — это наиболее сложный вид нейронных сетей, в которых имеется обратная связь. При этом под обратной связью подразумевается связь от логически более удалённого элемента к менее удалённому. Наличие обратных связей позволяет запоминать и… … Википедия

Источник