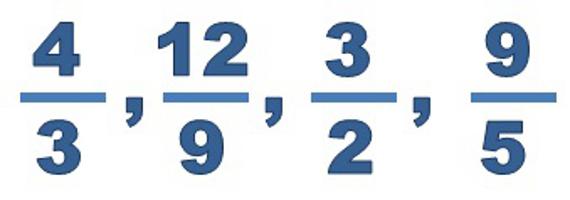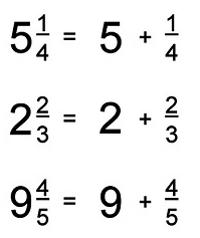Как сделать дробь неправильной дроби

Перевод смешанного или целого числа в неправильную дробь

Общие сведения о дробях

Дробь — форма записи рационального числа в виде доли целого.

В стандартном виде дроби записываются так: \( \frac mn.\)

Число над чертой называется числителем, под ней — знаменателем. Такую запись можно передать словами, как m частей из n, причем \(\frac nn\) равняется единице.

Например, \(\frac67\) — это 6 частей из 7.

В такой форме можно записать любое рациональное число, в том числе целое. При этом в качестве знаменателя может выступать любое натуральное число.

Так, единицу можно представить как \(\frac88,\;\frac<13><13>,\;\frac<857><857>\) и так далее.

Для записи чисел больше одного в дробной форме необходимо это число умножить на числитель:

Существует понятие правильных и неправильных дробей.

Правильной называют дробь, у которой модуль числителя меньше модуля знаменателя.

Соответственно, у неправильной дроби числитель больше или равен знаменателю. Из приведенных выше примеров \( \frac67\) — правильная дробь, а \(\frac88,\;\frac<13><13>,\;\frac<857><857>\) и \(\frac<10>5\) — неправильные.

Формы дробной записи

Как уже описывалось выше, стандартный способ записи обыкновенных дробей — через горизонтальную черту. Числитель помещается сверху, знаменатель — под чертой: \(\frac mn.\)

Один из самых распространенных и часто используемых на практике методов записи дробей — десятичная дробь. В этом случае число записывается как результат деления числителя на знаменатель. При этом, целая часть отделяется от остаточной при помощи запятой (в стандарте стран СНГ) или точкой.

По своей сути, все десятичные дроби являются смешанными числами.

Понятие смешанного числа

Смешанное число — комбинация целочисленной и дробной форм записи рациональных чисел.

Как соотносятся между собой неправильные дроби и смешанные числа

Неправильные дроби отличаются от правильных тем, что в них числитель больше знаменателя. То есть, если представлять их буквально как операцию деления, то делимое больше делителя. Это значит, что в них содержится целая часть, выделив которую можно получить смешанное число.

Необходимость и алгоритм преобразования

При решении задач зачастую необходимо преобразовать смешанные числа в дробные, так как с ними проще проводить вычисления.

Как перевести смешанное число в неправильную дробь

Чтобы записать смешанное число в форме неправильной дроби необходимо выполнить два действия: умножить целую часть на знаменатель и прибавить полученный результат к числителю.

Этот упрощенный способ преобразования работает на том принципе, что любое целое число можно представить в виде произведения этого числа на единицу. Единицу же в свою очередь можно представить в виде дроби, где числитель равен знаменателю. Разберем предыдущий пример более подробно:

Как выделить из неправильной дроби целую часть

Обратное преобразование работает на принципе, согласно которому, при делении двух некратных друг другу чисел, делимое можно представить в виде суммы кратного делителю числа и некоего остатка. В качестве примера возьмем число из предыдущего пункта:

В этом преобразовании можно пойти дальше и представить смешанное число в виде десятичной дроби. Для этого целая часть отделяется запятой, а операция деления продолжается с остатком, умноженным на 10. Само деление продолжается до тех пор, пока остаток не окажется равен нулю.

В случае с бесконечными десятичными дробями, деление продолжается до тех пор, пока число знаков после запятой не удовлетворит условие задачи. В таком случае, последняя цифра округляется согласно установленным правилам.

Работы любой сложности

Квалифицированная помощь от опытных авторов

Источник

Изучение основных правил умножения: как из неправильной дроби сделать правильную

Огромный блок математики посвящен работе с дробями или нецелыми числами. С ними очень часто встречаются и в жизни, поэтому знать, как работать с такими цифрами важно для любого человека. Математика – это наука, в которой ученик начинает с познания простых вещей и действий, а затем переходит к более сложным….

Знание и умение работать с подобными цифрами облегчит ему в дальнейшем работу с логарифмами, рациональными показателями и интегралами. С такими числами можно делать все то же самое, что и с обыкновенными: складывать дроби, делить, вычитать и умножать. Кроме этого, их можно сокращать. Работать с дробями просто, главное – это знать основные правила и методы их вычисления.

Основные понятия

Для того, чтобы понять, что это за значение такое, необходимо представить некий целый предмет. Допустим, что есть торт, который порезали на несколько одинаковых или равных кусков. Каждый кусочек будет называться долей.

Важно! В случае с дробями, есть некое целое число, которое состоит из равных долей – отдельных меньших чисел.

Например, 10 состоит из 5 двоек, каждая двойка – это часть от десяти.

Доли имеют свои названия, в зависимости от их общего количества в целом числе: 10 может состоять из двух пятёрок или пяти двоек, в первом случае она будет называться (одна вторая) , а во втором (одна пятая). Следует помнить, что равняется половине числа, (одна третья) трети, а (одна четвертая) – четвертью. Их могут также изображать через черточку: ½, 1/3 или 1/5.

Цифру, написанную сверху горизонтальной линии или слева от наклонной, называют числителем – он показывает сколько долей взяли у целого числа, а цифра под линии или справа от нее – знаменатель, он показывает на сколько всего долей разделили. Например, торт разделили на 10 кусков и сразу отложили два из них для опоздавших гостей. Это будет 2/10 (две десятых), т.е. взяли 2 (числитель) куска от общих 10 (знаменатель).

Дроби

Какие бывают доли, что такое неправильная дробь, что такое обыкновенная дробь? На эти вопросы легко ответить:

Смешанная цифра всегда может трансформироваться в неправильную дробь и наоборот.

Главное свойство гласит: при умножении, а также деления делимого и делителя на одинаковый множитель, в целом величина дроби не изменится. Это свойство делает возможным все операции с дробями.

Как из неправильной дроби сделать правильную

Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения

Как сократить?

Главное правило гласит, что долевую цифру можно сократить поделить ее числитель и знаменатель на одинаковый делитель (отличный от 0) так, чтобы получилась новая цифра с меньшими параметрами, но равная исходной по величине. Исходя из этого правила можно понять, что дроби бывают сократимые и несократимые.

Сокращать можно при умножении дробных выражений друг на друга: * . Сами по себе эти числа несократимые, но выполняя операцию умножения, можно сократить их по диагонали: * = = . Сокращать при умножении можно только крест-накрест: числитель первой со знаменателем второй, и наоборот.

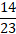
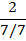
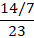
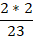
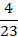
Сокращать можно и смешанную цифру, т.е. целую часть и правильную дробь представить в виде неправильной. Для этого следует выполнить некоторые действия:

Справедливо и обратное действие: из неправильной дроби сделать смешанную. Для этого рассмотрим обратное действие с :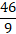

Таким способом сокращать дроби при любых операциях возможно. Можно сокращать значения ее делимого и делителя при умножении их на одинаковый множитель, и превращая из смешанного числа в долю, и наоборот.

Сокращение дробей

Возможные действия

Все основные виды вычислений доступны при счете долей, как и с целыми цифрами: сложение, вычитание и прочие. Рассмотрим каждое действие по отдельности с примерами:

Сложение и вычитание

Складывать доли можно двумя путями, в зависимости от их делителя. Они бывают одинаковыми и разными. Рассмотрим пример складывания долей с одинаковыми делителями.

Для решения + необходимо по отдельности сложить делимое долей, а делитель не трогать: 1+1. Результатом станет цифра , но поскольку она неправильная, то ее можно преобразовать в смешанную, разделив делимое на делитель: 2:2= 1. Неправильную долю всегда (!) следует приводить к правильной и несокращаемой, т. е. если ее делимое и делитель можно поделить на одинаковый множитель – это следует сделать в обязательно порядке.

В случае сложения долей с различными делителями, их необходимо изначально привести к одинаковому. Например, для решения : 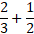необходимо:

Вычитание осуществляется точно так же: в случае с одинаковыми делителями их не трогаем, а числители последовательно вычитаем: = = . Если же знаменатели различные, то следует поступить, как и при сложении: найти НОК, множители, умножить доли, а затем вычесть уже доли с одинаковыми делителями.

Сложение дробей

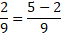
Умножение и деление

При умножении необходимо последовательно перемножить их верх и низ между собой: 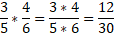= поскольку есть возможность сокращения на 6. В случае деления все несколько сложнее.

Для деления 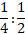следует:

Важно! Деление всегда можно заменить умножением, но только при соблюдении условия замены делителя на обратное ему число.

Перевод смешанного числа в неправильную дробь

Выделение целой части из неправильной дроби

Чтобы правильно решать подобные примеры, следует запомнить главное свойство и правила сокращения. Что касается операций, то важно знать, как правильно складывать и умножать при одинаковых и разных знаменателях, поскольку делятся и вычитаются они по одинаковому принципу.

Источник

Общие сведения

Слово «дробь» в обиход ввёл математик средневековой Европы Фибоначчи. На Руси под этим понятием понимались доли чисел. В дословном переводе на русский с арабского термин обозначает «ломать» или «раздроблять». Вид записи выражения, который применяется и сегодня, предложили арабы. Но фундамент теории заложили греческие и индийские учёные.

В математике под дробным отношением понимают число, образованное из некоторой части единицы. Простыми словами это можно объяснить на наглядном примере. Пусть на столе лежит две круглые пиццы. Каждую из них разрезали на восемь равных частей. Всего получилось шестнадцать долей. Через какое-то время было съедено одиннадцать кусков. Соответственно на столе осталось пять. В математической записи такое действие будет выглядеть как 11 / 8.

Число, стоящее в верхней части выражения, называют делимым или числителем, а в нижней делителем или знаменателем. В зависимости от их числового значения все дроби разделяют на три класса:

Кроме этого, выделяют ещё одну группу выражений. Дроби, относящиеся к ней, называют десятичными. Это такие отношения, у которых знаменатель — это десятичное число, стоящее в любой натуральной степени. Для записи десятичных выражений используют не дробную черту, а запятую. Например, 12 / 10 = 1,2.

Суть отношения

Обыкновенная дробь может быть правильной или неправильной. Например, 19 / 21 — правильное выражение, так как результат деления будет меньше единицы. В то же время обыкновенные числа 32 / 6 и 90 / 90 — неправильные, так как ответ, получаемый при делении, будет больше единицы в первом случае и равен ей во втором.

Чтобы разобраться, почему же дробные выражения, у которых числитель превосходит или равняется знаменателю называют «неправильными» можно порассуждать следующим образом.

Пусть имеется неправильная дробь 10 / 10. Эта запись обозначает, что взято десять долей чего-то состоящего из такого же числа частей. Иными словами, из имеющихся десяти долей можно сложить целый предмет. Неправильное выражение вида 10 / 10, по сути, означает целый предмет. Значит, можно записать, что 10 / 10 =1. Следовательно, такое отношение можно заменить натуральным числом.

Теперь можно рассмотреть неправильные отношения 7 / 3 и 12 / 4. Совершенно очевидно, что из этих семи третьих долей легко составляется два целых числа. Одно из них будет содержать три части. Значит, для оставшихся двух долей понадобится шесть частей: 3 + 3 = 6. При этом останется ещё одна доля — третья. Таким образом, выражение семь третьих означает две целые части и ещё одну третью от них. Аналогично из двенадцати четвёртых можно сформировать три целых числа по четыре доли в каждом. То есть дробное отношение 12 / 4 означает, по сути, три целых предмета.

Если провести анализ полученных результатов, то можно сделать вывод о том, что неправильные дроби, могут быть представлены в двух видах:

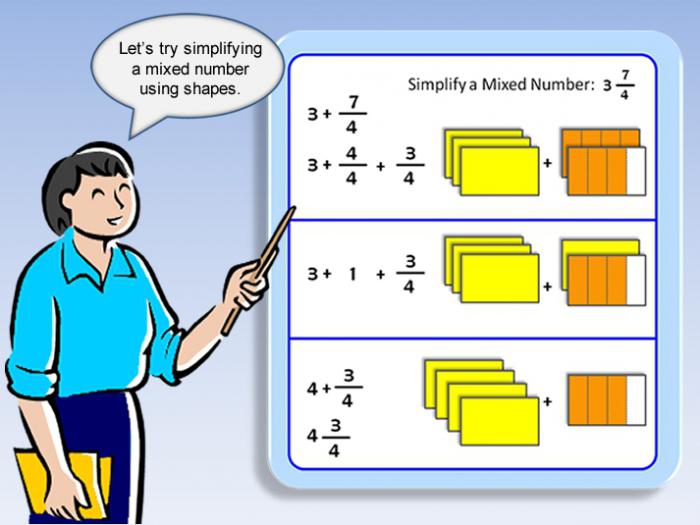
Особенный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной части. Это действие называется выделением целой доли из неправильного отношения. Причём такая операция может быть выполнена и в обратном направлении — трансформация выражения в смешанное.

Превращение дробей

По смыслу неправильные выражения представляют собой целую и дробную часть, записанную в виде отношения. Поэтому любую смешанную дробь можно превратить в правильную, и наоборот. Деление целого числа на такое же можно объяснить так. Пусть нужно разделить четыре на пять. Значит, единицу понадобится разделить на пять равных частей, то есть 1 / 5. Четыре же единицы дадут 1 / 5 + 1/ 5 + 1 / 5 + 1 / 5 = 4 / 5. В этом случае получается правильное выражение. Но бывает, что числитель количественно превышает знаменатель. Значит, для более понятной формы записи нужно из такого выражения выделить целую часть.

Например, нужно преобразовать число 25 / 8. Это действие подразумевает нахождение целых единиц, содержащихся в выражении. Рассуждать нужно следующим образом. Одна единица может быть представлена как 8 / 8, две — 16 / 8, три — 24 / 8. Значит, число состоит из трёх единиц и оставшейся 1 / 8 части. Поэтому записать его можно так: 3 (1 / 8).

Такого вида преобразования часто приходится выполнять при решении примеров с дробями в 5 классе. Поэтому понять принцип превращения лучше всего на конкретное задание. При этом можно использовать следующий алгоритм:

Итак, пусть имеется выражение 3 (5 / 7). Так как фактически это сумма трёх и пяти седьмых, то следуя алгоритму, можно решение расписать так: 3 + 5 / 7 = (3 * 7 + 5) / 7 = (21 + 5) / 7 = 26 / 7. Аналогичный результат мог быть получен при простом сложении двух частей смешанного числа: 3 / 1 + 5 / 7 = (3 * 7) / 1 * 7 + 5 / 7 = 21 / 7 + 5 / 7 = (21 + 5) / 7 = 26 / 7. Первый вариант, конечно же, более удобен. Его можно выразить формулой: a (c / d) = (a * d + c) / d.

Эту выражение нужно обязательно запомнить, так как его придётся довольно часто использовать при решении задач различной сложности.

Выполнение действий

Отличие неправильной дроби от правильной заключается в том, что первая равна или больше единицы, а вторая меньше её. Поэтому правило выполнения арифметических действий одинаковое для этих двух групп. Для того чтобы ребёнок понял, как правильно решать простые и сложные задания объяснение в 5 классе неправильных дробей и действий над ними начинают с повторения правила разложения числа на простые множители.

Выполняется оно за несколько шагов. Вначале ищут минимальную величину, на которую можно разделить исходное без остатка. Далее, находят результат деления и повторяют действие, но уже для полученного числа. Операцию повторяют до тех пор, пока в ответе не получится единица.

Разложение на простые множители используется при поиске наименьшего знаменателя при сложении или вычитании неправильных дробей с разными делителями. Существует алгоритм, придерживаясь которого можно выполнить любое арифметическое действие над двумя и более дробными выражениями. Он заключается в следующем:

Например, 4 / 3 + 9 / 7 = (7 * 4) / 21 + (3 * 9) / 21 = 28 / 21 + 27 / 21 = (28 + 27) / 21 = 55 / 21 = 2 (13 / 21) и 56 / 9 — 6 / 9 = (56 — 6) / 9 = 50 / 9 = 5 (5 / 9).

Неправильные выражения можно не только складывать, но и вычитать. Для того чтобы их перемножить следует отдельно найти произведение делимых и делителей. Затем в числитель записать первый результат, а в знаменатель второй. То есть действие нужно выполнять по формуле: f / n * s / m = (f * s) / (n * m). Выполнить деление также просто. Для этого действия в вычитаемом выражении меняется местами аргументы и выполняется умножение: (f / n) / (s / m) = (f * m) / (n * s).

Источник

Неправильные дроби: как научиться решать с ними примеры?

Какие виды дробей существуют?

Для начала о том, что это такое. Дробь — число, которое имеет некоторую часть от единицы. Ее можно записать в двух видах. Первый носит название обыкновенной. То есть такая, у которой есть горизонтальная или наклонная черта. Она приравнивается к знаку деления.

В такой записи число, стоящее над черточкой, называется числителем, а под ней — знаменателем.

Среди обыкновенных выделяют правильные и неправильные дроби. У первых числитель по модулю всегда меньше знаменателя. Неправильные потому так и называются, что у них все наоборот. Значение правильной дроби всегда меньше единицы. В то время как неправильная всегда больше этого числа.

Есть еще смешанные числа, то есть такие у которых имеются целая и дробная части.

Второй вид записи — десятичная дробь. О ней отдельный разговор.

Чем отличаются неправильные дроби от смешанных чисел?

По своей сути, ничем. Это просто разная запись одного и того же числа. Неправильные дроби после несложных действий легко становятся смешанными числами. И наоборот.

Смешанное число еще сравнивают с суммой целой части и дробной. Причем вторая всегда меньше единицы.

Как представить смешанное число в виде неправильной дроби?

Если требуется выполнить какое-либо действие с несколькими числами, которые записаны в разных видах, то нужно сделать их одинаковыми. Один из методов — представить числа в виде неправильных дробей.

Для этой цели потребуется выполнить действия по такому алгоритму:

Вот примеры того, как записать неправильные дроби из смешанных чисел:

Как записать неправильную дробь в виде смешанного числа?

Следующий прием противоположен рассмотренному выше. То есть когда все смешанные числа заменяются на неправильные дроби. Алгоритм действий будет таким:

Примеры такого преобразования:

76/14; 76:14 = 5 с остатком 6; ответом будет 5 целых и 6/14; дробную часть в этом примере нужно сократить на 2, получится 3/7; итоговый ответ — 5 целых 3/7.

108/54; после деления получается частное 2 без остатка; это значит, что не все неправильные дроби удается представить в виде смешанного числа; ответом будет целое — 2.

Как целое число превратить в неправильную дробь?

Бывают ситуации, когда необходимо и такое действие. Чтобы получить неправильные дроби с заранее известным знаменателем, потребуется выполнить такой алгоритм:

Самый простой вариант, когда знаменатель равен единице. Тогда ничего умножать не нужно. Достаточно просто написать целое число, которое дано в примере, а под чертой расположить единицу.

Пример: 5 сделать неправильной дробью со знаменателем 3. После умножения 5 на 3 получается 15. Это число будет знаменателем. Ответ задания дробь: 15/3.

Два подхода к решению заданий с разными числами

В примере требуется вычислить сумму и разность, а также произведение и частное двух чисел: 2 целых 3/5 и 14/11.

В первом подходе смешанное число будет представлено в виде неправильной дроби.

После выполнения действий, описанных выше, получится такое значение: 13/5.

Для того чтобы узнать сумму, нужно привести дроби к одинаковому знаменателю. 13/5 после умножения на 11 станет 143/55. А 14/11 после умножения на 5 примет вид: 70/55. Для вычисления суммы нужно только сложить числители: 143 и 70, а потом записать ответ с одним знаменателем. 213/55 — эта неправильная дробь ответ задачи.

При умножении 13/5 и 14/11 не нужно приводить к общему знаменателю. Достаточно перемножить попарно числители и знаменатели. Получится ответ: 182/55.

Так же и при делении. Для правильного решения нужно заменить деление на умножение и перевернуть делитель: 13/5 : 14/11 = 13/5 х 11/14 = 143/70.

Во втором подходе неправильная дробь обращается в смешанное число.

После выполнения действий алгоритма 14/11 обратится в смешанное число с целой частью 1 и дробной 3/11.

Во время вычисления суммы нужно сложить целые и дробные части по отдельности. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Итоговый ответ получается 3 целых 48/55. В первом подходе была дробь 213/55. Проверить правильность можно, переведя его в смешанное число. После деления 213 на 55 получается частное 3 и остаток 48. Нетрудно заметить, что ответ правильный.

Для нахождения произведения и частного пользоваться смешанными числами неудобно. Здесь всегда рекомендуется переходить к неправильным дробям.

Источник