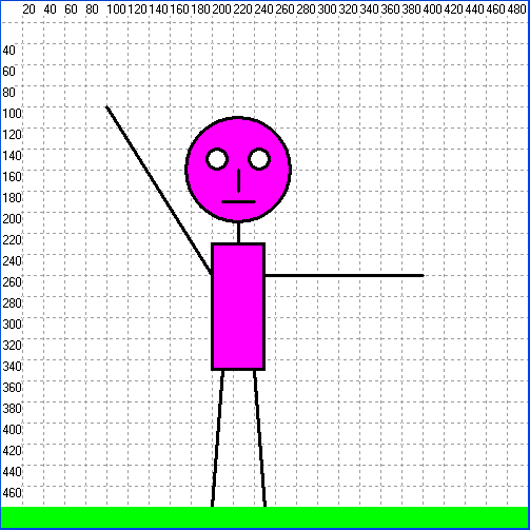Как сделать движение в паскале

Организация движения объектов на графическом экране в программе Турбо Паскаль

Тип урока: Урок формирования знаний.

Цели урока: Познакомить учащихся с понятием анимации. Сформировать умение организовывать перемещение фрагментов рисунка на экране в программе Турбо Паскаль.

Образовательный аспект:

Учащиеся должны уметь:

Развивающий аспект: Развитие представления о возможности создания простой анимации в программе Turbo Pascal при помощи стандартных процедур и кодов клавиш.

Воспитательных аспект: Воспитывать у учащихся гармоничное восприятие компьютерных технологий.

Программная поддержка: программа Turbo Pascal.

Раздаточный материал:

Ход урока

1 Организационный этап (3 минуты):

1.1 Приветствие учащихся.

1.2 Отметить отсутствующих.

1.3 Постановка цели и задач урока.

Цель урока – организация движения фрагментов рисунка на экране.

Для достижения задуманной цели необходимо выполнить следующие задачи:

2 Повторение ранее изученного материала (5 минут):

2.1 Раздача материала («Карточки с таблицей основных процедур для модуля Graph», «Карточки с таблицей кодов клавиш»).

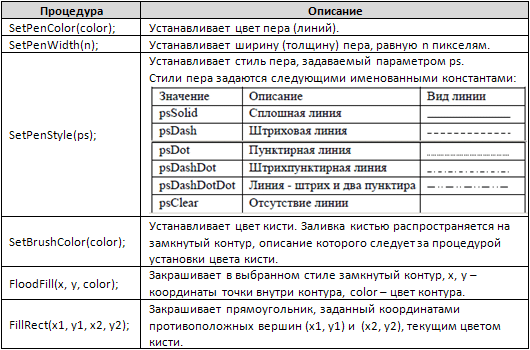
Карточка с таблицей основных процедур для модуля Graph

Заголовок процедуры

Пояснение к процедуре

Построение окружности с центром (х,у) и радиусом r

Соединение двух точек отрезками

Цвет объекта рисунка

Очистка фрагментов рисунка

Вывод текста, начиная с точки Х,У

Карточка с таблицей кодов клавиш

Клавиша управления

Код клавиши

2.2 Учащимся предлагается вспомнить основные графические процедуры, изученные на прошлых уроках (карточка с таблицей основных процедур для модуля Graph). Также учащиеся должны вспомнить параметры данных процедур.

3 Изучение нового материала (15 минут):

3.1 Запуск и демонстрационный показ программы «Перемещение неваляшки» в программе Turbo Pascal с помощью мультимедийного проектора (выполняет учитель).

3.2 Учащимся предлагается изучить карточку с таблицей кодов клавиш. На данном этапе изучения темы нужно обратить внимание учащихся на то, что код клавиши указывается символом # («решётка») и определенным числом, поэтому в программе коды клавиш также имеют символьный тип.

Учащимся предлагается изучить карточку с листингом программы «Перемещение неваляшки»:

Карточка с листингом программы «Перемещение неваляшки»

program Animation;
uses crt, graph;
const a=5;
var gd,gm,x,y:integer;
ch:char;
procedure anima(x1,y1:integer);
begin
setcolor(14);
circle(x1,y1,20);
setcolor(10);
circle(x1-6,y1-6,2);
circle(x1+6,y1-6,2);
circle(x1+2,y1+50,30);
circle(x1-30,y1+30,8);
circle(x1+33,y1+28,8);
setcolor(11);
line(x1-5,y1+10,x1+5,y1+10);
OutTextXY(250,150,’Hello. ‘)
end;
begin
gd:=detect;
initgraph(gd,gm,’c:\bp\bgi’);
x:=getmaxx div 2; y:=getmaxy div 2;
anima(x,y);
repeat
ch:=readkey; if ch=#0 then ch:=readkey;
case ch of
#75:x:=x-a; #77:x:=x+a; #72:y:=y-a; #80:y:=y+a;
end;
cleardevice;
anima(x,y);
until ch=#27;
closegraph; end.

Изучение фрагмента программы «procedure anima»: Обратить особое внимание на процедуру anima, которая непосредственно выполняет прорисовку отдельных частей неваляшки: голова, глаза, рот, нос, «ручки».

4 Компьютерный практикум (13 минут):

4.1 Учащиеся рассаживаются за компьютеры.

4.2 Запускают программу Turbo Pascal.

4.3 Создают новый документ.

4.4 Печатают листинг программы«Перемещение неваляшки».

4.5 Сохраняют документ программы.

4.6 Запускают программу «Перемещение неваляшки».

Учитель контролирует выполнение работы, и в случае появления проблемы помогает учащимся.

5 Этап подведения итогов (2 минуты).

Учащиеся демонстрируют свои программы учителю. Если остаётся время, то пытаются изменить некоторые параметры частей рисунка (увеличение объектов, изменение цвета частей рисунка).

6 Домашнее задание (2 минуты).

На выбор составить процедуру для одного из предложенных пунктов, для того, чтобы на следующем уроке произвести закрепление изученного материала:

Источник

Управление движением мячика

Графика. Управление движением объектов с клавиатуры
Есть куча Line, Circle, Arc и тд, т.е. некий рисунок, ему нужно придать жизнь т.е. что бы он начал.

Движение, вращение, управление движением, управление вращением фигуры
Написать программу, выполняющую четыре операции над графическим.

Виталий777555, попробуйте так:

выдает ошибку «Прекращена работа программы»((((
Вы написали на PascalABC,а не PascalABC.NET

Добавлено через 21 час 57 минут
Со вторым и первым вопросом я разобрался) Помогите решить первый вопрос)

Вложения

graph.zip (1.11 Мб, 25 просмотров)

большое спасибо, уже лучше) Для первой игры думаю пойдет, со временем научусь чтобы действовали все восемь направлений как в игре колобок)Мне преподаватель по программированию говорит, что писать игры это хорошая тренировка для начинающего программиста)

Добавлено через 7 часов 24 минуты
Всем спасибо за внимание, все проблемы добил до конца

Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь.

Управление движением
Вопрос в следующем: хотел сделать, чтобы марио двигался только по зеленным и синим квадратам.

Управление движением объекта на форме
Здравствуйте! Решил написать небольшую игру, но так как в билдере новичок столкнулся с задачей. У.

Управление движением с помощью клавиш
сделать прогу управ движ * по экрану с помощью клавиш влево вправо вверх вниз

Задача моделирования и управление движением
Суть в том что, клетка находится изначально в любой клетке(например в верхней) и пользователь.

Источник

Работа с графикой в PascalABC

После запуска PascalABC, по умолчанию, запускается текстовый режим. Для работы с графикой служит отдельное графическое окно.

Чтобы его открыть, необходимо подключить модуль GraphABC. В этом модуле содержится набор процедур и функций, предназначенных для работы с графическим экраном, а также некоторые встроенные константы и переменные, которые могут быть использованы в программах с графикой.

С их помощью можно создавать разнообразные графические изображения и сопровождать их текстовыми надписями.

Подключение осуществляется в разделе описаний.
Формат подключения модуля GraphABC:Uses GraphABC;

Графический экран PascalABC (по умолчанию) содержит 640 точек по горизонтали и 400 точек по вертикали. Начало отсчета – левый верхний угол экрана. Ось x направлена вправо, а ось y –вниз. Координаты исчисляются в пикселях.

Все команды библиотеки GraphABC являются подпрограммами и описаны в виде процедур и функций. Для того, что бы команда выполнилась необходимо указать команду и задать значения параметров.

Управление графическим окном

После запуска PascalABC, по умолчанию, запускается текстовый режим. Для работы с графикой служит отдельное графическое окно.

Чтобы его открыть, необходимо подключить модуль GraphABC. В этом модуле содержится набор процедур и функций, предназначенных для работы с графическим экраном, а также некоторые встроенные константы и переменные, которые могут быть использованы в программах с графикой.

С их помощью можно создавать разнообразные графические изображения и сопровождать их текстовыми надписями.

Подключение осуществляется в разделе описаний.
Формат подключения модуля GraphABC:Uses GraphABC;

Графический экран PascalABC (по умолчанию) содержит 640 точек по горизонтали и 400 точек по вертикали. Начало отсчета – левый верхний угол экрана. Ось x направлена вправо, а ось y –вниз. Координаты исчисляются в пикселях.

Все команды библиотеки GraphABC являются подпрограммами и описаны в виде процедур и функций. Для того, что бы команда выполнилась необходимо указать команду и задать значения параметров.

Процедуры рисования графических примитивов

Процедуры, используемые для работы с цветом

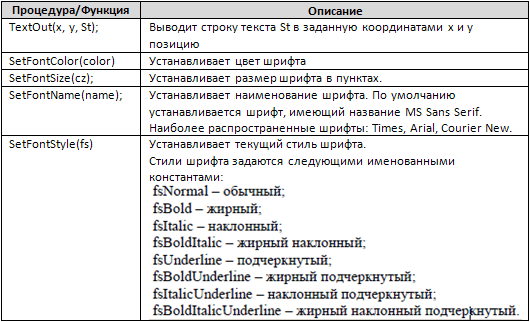
Процедуры для работы с текстом

Цвета в PascalABC

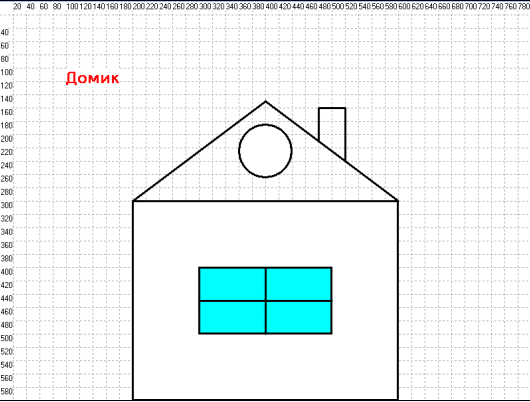
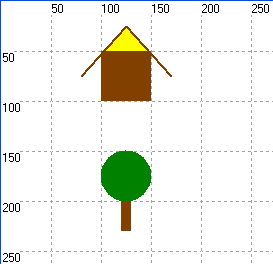
Пример графической программы, рисующей изображение дома:

Рисунок в PascalABC

Программа, рисующая фигурку:

Практическая работа за компьютером

Задание 1. Определите координаты и составьте программу, выводящую на экран рисунок дома и дерева.

Программа будет иметь вид:

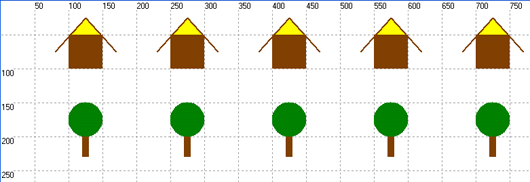
Задание 2. Используя оператор цикла и введя переменную для пересчета координат по оси x, постройте “поселок”, состоящий из 5 домов. Внесите соответствующие дополнения и изменения в предыдущую программу.

Весь наш «поселок» выстроился вдоль горизонтальной оси экрана — оси X. Построение рисунка начинается с левого верхнего угла стены первого дома — точки с координатами (100, 50). Координата Y не изменяется. Чтобы начать рисовать второй домик, нужно координату X увеличить на 150 (50 точек — ширина первого дома и 100 точек — расстояние между домиками).

Выберем в качестве параметра цикла целочисленную переменную X.
Для всех элементов нашего рисунка абсолютное значение координаты X заменим на относительное. Например, для стены дома процедура для рисования запишется следующим образом:

Отличное подспорье в подготовке к уроку. Спасибо

Большое спасибо.Хорошо представлен материал, удобнее чем в справке языка.

Спасибо! Доступно и методически грамотно изложено.

Спасибо большое! Просто и доступно!

Прекрасно и доходчиво изложен материал.Очень мне помог.Спасибо

Давно пользуюсь Вашими разработками. Большое спасибо.
Ищу урок о преобразовании компьютерной системы координат в математическую в PascalABC.
Для Visual Basic у Вас такой урок есть.

Очень помогло!! спасибо за такую информацию

Источник

Графика и анимация в Паскаль АВС
план-конспект урока

Данная разработка предназначена для учащихся 7-9 классов, изучающих программирование на языке Паскаль. Уроки позволят освоить элементы графики и анимации в ПаскальАВС. Процесс создания графики вызывает у учащихся особый интерес. Подобные уроки формируют у учащихся пространственное воображение, умение работать с координатной плоскостью, развиваются навыки программирования, а также способствуют развитию воображения и логического мышления, формированию чувства композиции и художественно-графических умений, навыков конструирования и проектирования, приобщению к творческому процессу и развитию терпения и трудолюбия.

Скачать:

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Предварительный просмотр:

Цель : закрепление и систематизация знаний и умений учащихся при работе с графикой в Паскаль АВС.

Тип урока : закрепления знаний.

Формы работы : фронтальная, индивидуальная.

Методы работы : частично-поисковый, репродуктивный.

Оборудование урока : ПК, мультимедийный проектор

Требования к результатам усвоения учебного материала.

Ученики должны знать:- язык программирования PascalАВС

— особенности работы в графическом режиме GraphАВС;

— стандартные процедуры и функции модуля GraphАВС;

— графические операторы языка программирования

Ученики должны уметь:

— строить элементарные изображения;

— работать в графическом режиме;

— правильно применять стандартные процедуры и функции модуля GraphАВС;

— применять базовые алгоритмические структуры при программировании

-производить необходимые действия с программой;

Прямоугольник в Паскале рисуется:

Треугольник рисуется процедурами:

Окружность можно нарисовать с помощью процедуры:

Ф УНКЦИЯ RANDOM ДЛЯ ИСПОЛЬЗОВАНИЯ ОКРАСКИ

 SetPenColor(rgb(random(256), random(256), random(256))); — выбирает случайное число из 256-цветной палитры для красного, зеленого и синего.

* раскрасить круги случайным цветом

Задание 4: «Круги на воде».
Нарисуйте пару десятков концентрических окружностей, то есть окружностей разного радиуса, но имеющих общий центр.

Задание 5:
Воспроизвести изображение при помощи программы:

Пример графической программы, рисующей изображение дома:

uses Graphabc; //подключение модуля GraphABC

SetWindowWidth ( 800 ) ; //ширина окна программы

SetWindowHeight ( 600 ) ; //высота окна программы

SetPenWidth ( 3 ) ; //толщина пера

SetFontSize ( 18 ) ; //размер шрифта

SetFontColor ( clRed ) ; //цвет шрифта

SetFontStyle ( fsBold ) ; //жирный стиль шрифта

SetBrushColor ( clAqua ) ; //цвет заливки окна

Рисунок в PascalABC

Программа, рисующая фигурку:

SetPenWidth ( 3 ) ; //устанавливаем стиль пера

SetBrushColor ( clFuchsia ) ; //устанавливаем цвет кисти

Задание 1. Определите координаты и составьте программу, выводящую на экран рисунок дома и дерева.

Весь наш «поселок» выстроился вдоль горизонтальной оси экрана — оси X. Построение рисунка начинается с левого верхнего угла стены первого дома — точки с координатами (100, 50). Координата Y не изменяется. Чтобы начать рисовать второй домик, нужно координату X увеличить на 150 (50 точек — ширина первого дома и 100 точек — расстояние между домиками).

Выберем в качестве параметра цикла целочисленную переменную X.
Для всех элементов нашего рисунка абсолютное значение координаты X заменим на относительное. Например, для стены дома процедура для рисования запишется следующим образом:

Сформулируем условие выполнения циклических действий для нашей задачи.

Какие координаты имеет левый верхний угол пятого дома? Конечное значение выбранного нами параметра цикла x = 700. Тогда условие выполнения цикла записывается так: x

Словесное описание алгоритма коротко можно записать так:

Переменной цикла x присвоить начальное значение 100. Пока x

Самостоятельно составить программу.

Предварительный просмотр:

Урок 3. Анимация в Паскале

Цель: Изучить построение анимации в Паскаль

Образовательные задачи: Познакомить с понятием «Анимация»,

Закрепить знания детей об алгоритме построения анимации.

Задачи воспитания : Воспитать трудолюбие, самостоятельность, культуру речи, и общения.

Задачи развития: Развивать мышление, память, речь и другие психические процессы.

Тип урока: Формирование новых знаний и их закрепление.

Оборудование: Компьютеры, интерактивная доска, проектор, презентация.

Методы обучения: Иллюстративно-обьяснительный

Оборудование урока : ПК, мультимедийный проектор,язык программирования Паскаль АВС.

Анимация в программировании заключается в том, что сначала рисуется фигура цветным инструментом, затем с тем же координатами рисуется та же фигура белым цветом. После чего происходит сдвиг фигуры и действия повторяются.

В этом уроке будет показано, как можно создать анимированное изображение с помощью модуля GraphABC.

Пример: Воспроизвести движение круга по горизонтали.

Теперь рассмотрим пример: создать движение нескольких (примитивных) фигур по заданной траектории.

Без чего мы обойтись не сможем, не сможем мы обойтись без нескольких инструментов:

Рисование средствами PascalABC происходит очень медленно. Пока оно идет, картинка на экране успевает много раз обновиться. Отсюда мерцание. То есть, мы видим не окончательную картинку, а процесс ее рисования. Окончательную картинку в общем-то не видим — как только она построилась, мы ее тут же стираем и начинаем новый цикл рисования. Для борьбы с этим эффектом придумали двойную буферизацию. Идея в том, чтобы сначала построить картинку в памяти (не выводя на экран), а затем отобразить новый кадр на экране целиком, без промежуточных вариантов, где не хватает половины лучиков. Для этого в начале программы вызываем процедуру LockDrawing.

Процедура ClearWindow (color);

После каждой прохода по циклу очищает графическое окно указанным цветом, который передается в качестве параметра.

После этого все команды рисования будут создавать картинку в памяти (в так называемом вторичном буфере). Непосредственно на экране ничего рисоваться не будет. После того, как очередной кадр анимации полностью отрисован (то есть перед ClearWindow), нужно вызвать процедуру Redraw;

Эта процедура вызовет перерисовку всей картины.

Нарисуем сначала четыре окружности.

//Отрисовка четырех окружностей.

Второй стадией, будет отрисовка пятой окружности и с помощью вышеуказанных процедур и цикла заставим его двигаться по заданной траектории.

//Движение от первой точки до второй

for i := 100 to 300 do

//Движение от второй точки до третьей

for i := 100 to 300 do

//Движение от третьей точки до четвертой

for i := 300 downto 100 do

//Движение от четвертой точки до первой

for i := 300 downto 100 do

Задание 6: Выполнить анимацию движения квадрата по следующей траектории:

Задача №7 Создать проезжающий грузовик

По теме: методические разработки, презентации и конспекты

Презентацию можно использовать для демонстрации эффектов анимации, используемых в MS Power Point.

Описывает технологию создания анимации в программе Macromedia Flash.

Разработка урока предусматривающая работу в Паскале.

Материал предназначен для студентов 1 курса.

Данная разработка предназначена для учащихся 7-9 классов, изучающих программирование на языке Паскаль.Уроки позволят освоить элементы графики и анимации в ПаскальАВС. Процесс создания графики вызывает.

Материал для проведения расчетов по математике на тему Треугольник Паскаля.

Источник