Как сделать график линейной функции
Построение графика линейной функции. Визуальный гид (ЕГЭ – 2021)
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое линейная функция.
Начнем с небольшой проверки:
Приступим к покорению линий и графиков!
ШПОРА ПО ГРАФИКУ ЛИНЕЙНОЙ ФУНКЦИИ
График линейной функции – прямая линия. Прямую можно провести через две точки.
Чтобы построить график линейной функции вида \( \displaystyle y=kx+b\), нужно:
Пример для функции \( y=2x+1\):
Проще всего найти функцию, если аргумент: \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).
Итак, первая точка имеет координаты \( \left( 0;1 \right)\).
Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).
Вторая точка имеет координаты \( \left( 1;3 \right)\).
Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой. Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\)
\( \displaystyle k=tg\alpha =\frac
Построение графика линейной функции
Итак, ты уже умеешь обращаться с линейной функцией, анализировать ее график и строить его по точкам. Кстати, сколько нужно точек, чтобы построить график линейной функции?
Скажу сразу, эта тема настолько простая, что много нового ты здесь не выучишь. Но ты научишься не теряться во всяких нестандартных ситуациях.
Итак, дамы и господа, линейная функция:
Построение графика линейной функции: ты берешь два каких-либо икса, (например, \( \displaystyle 0\) и \( \displaystyle 1\)), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Но бывает, что функция задана по-другому, например, неявно. Сейчас разберем, как быстро справляться с такими ситуациями.
Пример неявно заданной линейной функции
Постройте график уравнения \( \displaystyle 2y+3x=6\).
Ну а что тут сложного? Чтобы произвести построение графика линейной функции выражаем y и строим по точкам.
Это да, но можно сделать проще и интересней!
Выясним, в какой точке эта прямая будет пересекать ось \( \displaystyle Ox\).
Что характерно для этой точке? Правильно, \( \displaystyle y=0\). Так и пишем:
\( \displaystyle 2\cdot 0+3x=6\text< >\Rightarrow \text< >x=2\)
А теперь проделаем то же самое с другой осью: в какой точке график пересекает ось \( \displaystyle Oy\)?
\( \displaystyle x=0\text< >\Rightarrow \text< >2y+3\cdot 0=6\text< >\Rightarrow \text< >y=3\)
Бум! Вот и они – две точки графика. Осталось только приложить линейку:
Согласись, это было быстро и просто!
А теперь сам:
Ладно, а как еще можно задать функцию?
Ну, например словесно:
Прямая проходит через точку \( \displaystyle A\left( 2;3 \right)\), а ее угловой коэффициент равен \( \displaystyle 0,75\).
Ну что же, вспоминаем: что такое угловой коэффициент?
Что такое угловой коэффициент
Это, с одной стороны, коэффициент при \( \displaystyle x\), а с другой – это тангенс угла между прямой и осью \( \displaystyle Ox\).
Вот это мы и используем когда делаем построение графика линейной функции: ставим точку \( \displaystyle A\), и рисуем прямоугольный треугольник так, что один его катет параллелен оси \( \displaystyle Ox\), а другой – перпендикулярен.
При этом второй катет должен быть ровно в \( \displaystyle 0,75\) раз больше первого.
Очень удобно в этом случае, чтобы первый катет был равен \( \displaystyle 4\), тогда второй будет равен \( \displaystyle 3\):
Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.
Регистрируйся здесь и приходи!
Разбор нескольких примеров построения графиков линейной функции
Пример №1
Прямая, уравнение которой имеет вид \( y=-2x+b\) (\( b\) неизвестно), проходит через точку \( M\left( 1;2 \right)\). Постройте ее.
Должно получиться вот так:
Пример №2
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
Строить график прямой \( y=-1,5x+1\) нельзя.
О, это что-то новенькое. Про параллельность прямых мы еще не учили.
Но как обычно, все просто. Нарисуем несколько параллельных прямых на координатной плоскости:
Что у них общего? Вообще, какие параметры важны для графиков? Конечно же, коэффициенты \( k\) и \( b\).
И сразу становится ясно: раз \( k\) отвечает за наклон, а наклон у них одинаковый (это же параллельные прямые, а ось \( Ox\) – секущая), значит, у них одинаковый коэффициент \( k\)!
Вернемся к задаче. Напомню условие:
Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).
График пересекает ось ординат в точке \( \displaystyle y=5,5\). Это и есть коэффициент \( \displaystyle b\):
Пример №3
Ответ: \( y=2x+4\).
Пройди эти 4 урока и ты научишься решать экономическую задачу любой сложности с самого нуля, шаг за шагом. Подробно о том, что входит в курс можно прочитать здесь.
Пример №4
И еще один тип прямых. Самый простой из всех.
Зарегистрируйся один раз и ты откроешь все 100 статей учебника
А также получишь доступ к видеоурокам и другим бесплатным материалам курса «Подготовка к ЕГЭ с репетитором»
* Если не понравятся бесплатные материалы, ты сможешь отписаться в любой момент
Хм… Даже на линейную функцию непохоже, чего это он самый простой?
А вот почему: достаточно небольшого преобразования, и получится самая обычная линейная функция:
А, нет, не все… еще ведь ОДЗ: на ноль делить нельзя, бла бла бла…
Это и есть все отличие от обычной прямой: просто надо будет выколоть из графика одну точку: \( y=x-5\).
Ответ: \( y=x-1,\text< >x\ne 2\)
P.S. Последний бесценный совет!
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут. Почему? Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем большинство твоих сверстников. Проблема в том, что этого может не хватить…
Для успешной сдачи ЕГЭ и поступления в ВУЗ мечты на бюджет и, самое главное, для жизни. Я не буду тебя ни в чем убеждать, просто скажу одну вещь… Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил.
Это статистика. Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Что нужно, чтобы сдать наверняка ЕГЭ, поступить в ВУЗ мечты и быть в конечном итоге… более счастливым? Две вещи.
Первое, тебе нужно набить руку, решая задачи
На экзамене у тебя не будут спрашивать теорию. Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка. “Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
И сейчас будет честная реклама наших курсов подготовки к ЕГЭ, потому что они решают обе эти проблемы.
Тебе же понятен этот учебник? Так вот наши курсы такие же понятные как этот учебник.
Потому что их подготовил и ведет автор этого учебника Алексей Шевчук.
Он буквально разжевывает все на вебинарах. Вы решаете задачи. Много задач. У вас будет проверка домашки и марафон «Год за месяц» в мае, чтобы «упаковать» ваши знания и улучшить результат на 20-30%.
Курсы очень бюджетные: от 2000 до 3990 тыс/мес за 12 двухчасовых занятий с Алексеем.
Кликайте по этим кнопкам и читайте условия, там все очень подробно описано:
Как построить график линейной функции
Как построить график линейной функции?
Графиком линейной функции является прямая. Для построения прямой достаточно знать две её точки. Следовательно, чтобы построить график линейной функции, нужно найти две любые точки, через которые он проходит.
Абсциссу, то есть координату x, для каждой точки выбираем сами. Удобно брать первой x=0. Следующую абсциссу желательно брать на расстоянии, не меньшем 2 единиц, например, x=2, или x=-2. Чем дальше друг от друга расположены точки, тем точнее получится график.
Если k и b — дроби, следует (по возможности) подбирать x таким образом, чтобы обе координаты (x;y) являлись целыми числами.
Построить график функции:
Это — линейная функция. Её графиком является прямая. Для построения прямой нужно взять две точки.
Полученные точки (0;-5) и (6;7) отмечаем на координатной плоскости и проводим через них прямую.
Точки (0;6) и (5;2) отмечаем на координатной плоскости и проводим через них прямую.
Точки (0;3) и (-7;-2) отмечаем на координатной плоскости и проводим через них прямую.
Точки (0;-7) и (-6;3) отмечаем на координатной плоскости и проводим через них прямую.
Это — частный случай линейной функции. Графиком является прямая, параллельная оси Ox. На оси Oy отмечаем точку (0;4) (можно отметить любую другую точку с ординатой y=4) и проводим через неё параллельно оси Ox прямую.
Другой частный случай линейной функции — прямую пропорциональность y=kx — рассмотрим отдельно.
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Парабола
Гипербола
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>
Если k 0, ветви гиперболы проходят через II и IV четверти.
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Алгоритм построения графика линейной функции
Линейная функция и ее график
1) Линейной функцией называется функция, которую можно задать формулой вида
3) Алгоритм построения графика линейной функции:
1) Найти координаты двух точек графика
2)Отметить полученные точки на координатной плоскости
3)Провести через полученные точки прямую
Построение графика линейной функции: ты берешь два каких-либо икса, (например, 0 и 1 ), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Линейная функция и ее график
1) Линейной функцией называется функция, которую можно задать формулой вида
3) Алгоритм построения графика линейной функции:
1) Найти координаты двух точек графика
2)Отметить полученные точки на координатной плоскости
3)Провести через полученные точки прямую
Построение графика линейной функции: ты берешь два каких-либо икса, (например, 0 и 1 ), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Линейная функция и ее график
1) Линейной функцией называется функция, которую можно задать формулой вида
3) Алгоритм построения графика линейной функции:
1) Найти координаты двух точек графика
2)Отметить полученные точки на координатной плоскости
3)Провести через полученные точки прямую
Построение графика линейной функции: ты берешь два каких-либо икса, (например, 0 и 1 ), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Линейная функция и ее график
1) Линейной функцией называется функция, которую можно задать формулой вида
3) Алгоритм построения графика линейной функции:
1) Найти координаты двух точек графика
2)Отметить полученные точки на координатной плоскости
3)Провести через полученные точки прямую
Построение графика линейной функции: ты берешь два каких-либо икса, (например, 0 и 1 ), подставляешь их в формулу, находишь соответствующие игреки.
Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.
Линейная функция и ее график
1) Линейной функцией называется функция, которую можно задать формулой вида
3) Алгоритм построения графика линейной функции:
1) Найти координаты двух точек графика
2)Отметить полученные точки на координатной плоскости
3)Провести через полученные точки прямую
Линейная функция и ее график
1) Линейной функцией называется функция, которую можно задать формулой вида
3) Алгоритм построения графика линейной функции:
1) Найти координаты двух точек графика
2)Отметить полученные точки на координатной плоскости
3)Провести через полученные точки прямую
Инклюзия в современном обществе и ее роль в социализации
идёт регистрация Успейте записаться до 2 февраля!
Номер материала: ДБ-668902
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
✅ На балансе занятий — 1
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Построение графиков функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Чтобы ребенок разобрался в теории и чувствовал себя увереннее на школьных контрольных, запишите его на современные уроки математики в онлайн-школу Skysmart.
Интерактивные задания, математические комиксы и карта прогресса в личном кабинете — математика еще никогда не была таким увлекательным приключением!
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
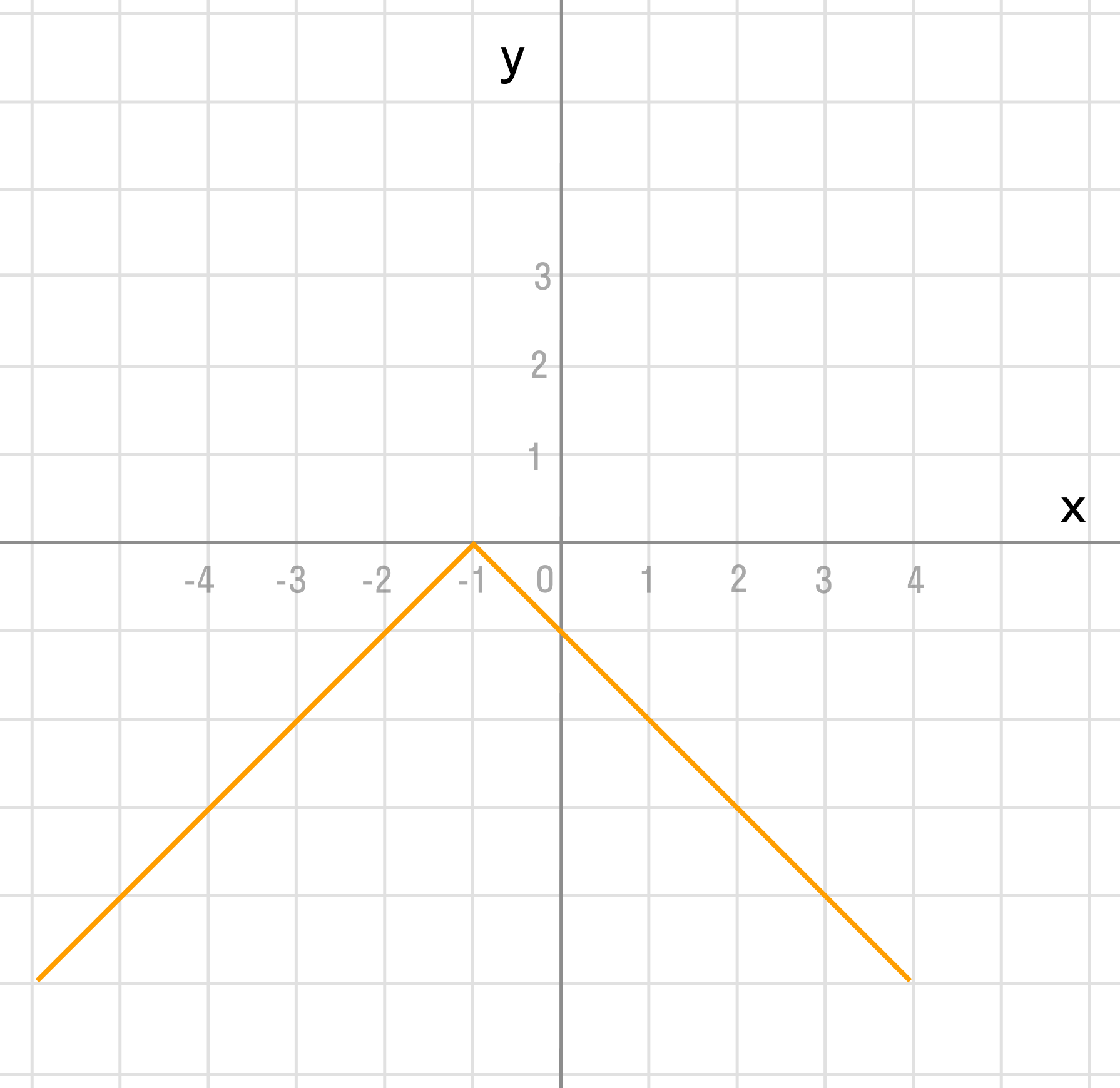
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

В детской школе Skysmart учиники чертят графики на специальной онлайн-доске. Учитель видит, как размышляет ученик и может вовремя его направить в нужную сторону.
Запишитесь на бесплатный вводный урок математики и занимайтесь в современном формате и с поддержкой заботливых учителей.