Как сделать сферу в mathcad
Построение графиков в MathCad
В статье рассмотрены основные возможности построения графиков в программе mathcad. Для инженерных и студенческих расчетов, как правило, достаточно знать следующие методы построения графиков:
Построение графика по точкам
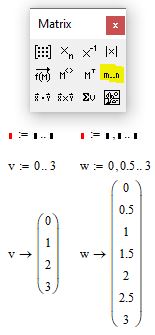
Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)
Рис. 1. Создание матриц-столбцов
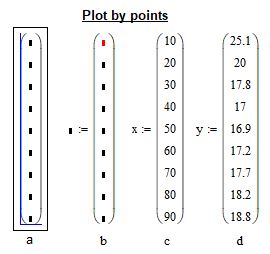
В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «:«. У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.
Рис. 2. Заполнение матриц-столбцов для графика
На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)
Рис. 3. Создание заготовки для графика
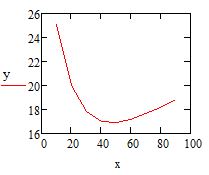
Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)
Рис. 4. График по точкам
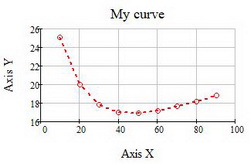
Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)
Рис. 5. Настройка отображения графика
Построение графика функции f(x)
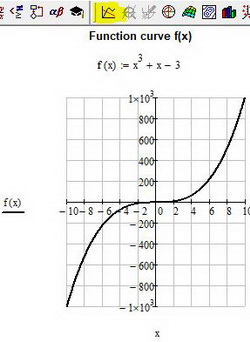
Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой
Рис. 6. Построение графика функции f(x)
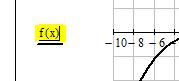

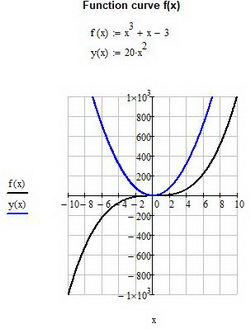
Рис. 7. Построение двух графиков функции
Построение эпюры в mathcad
Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:
— ввести функцию в виде y = f(x), как это показано в примерах выше;
— ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
— создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
— настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании
Рис. 8. Ввод ранжированной переменной
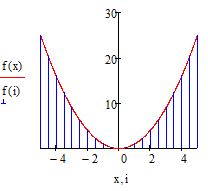
Ранжированные переменные можно использовать для построения эпюр распределения физических величин. Для этого постройте ваш исходный график одним из методов, описанных выше. Пусть это будет график f(x):=x^2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже
Рис. 9. Ввод ранжированной переменной
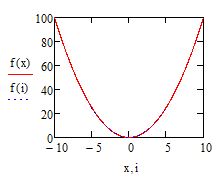
Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже
Рис. 10. Построение эпюры. Шаг 1
Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.
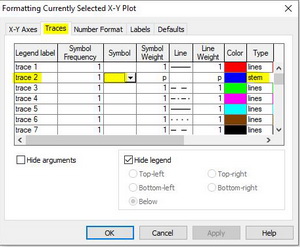
Рис. 11. Построение эпюры. Шаг 2
В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)
Рис. 12. Построение эпюры. Шаг 3
Построение графика в полярных координатах в mathcad
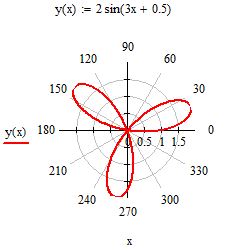
Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)
Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph
Рис. 13. Создание загатовки для графика в полярных координатах
Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.
Рис. 14. Построение графика в полярной системе координат
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Как сделать сферу в mathcad
Интерполяция использует значения некоторой функции, заданные в ряде точек, чтобы предсказать значения функции между ними. В Mathcad можно или соединять точки данных прямыми линиями (линейная интерполяция) или соединять их отрезками кубического полинома (кубическая сплайн-интерполяция).
В отличие от функций регрессии, обсуждаемых в следующем разделе, функции интерполяции определяют кривую, точно проходящую через заданные точки. Из-за этого результат очень чувствителен к ошибкам данных. Если данные зашумлены, следует рассмотреть возможность использования регрессии вместо интерполяции.
Линейное предсказание заключается в использовании существующих значений данных, чтобы предсказать значения за их пределами. В Mathcad есть функция, которая позволяет предсказывать будущие значения данных на основе уже имеющихся данных.
Всякий раз, когда массивы используются в любой из функций, описанных в этом разделе, убедитесь, что каждый элемент массива содержит определённое значение, так как Mathcad присваивает значение 0 любым элементам, которые явно не определены.
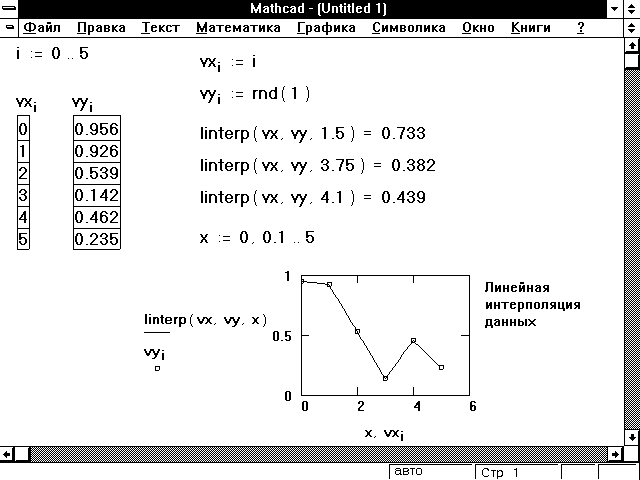
При линейной интерполяции Mathcad соединяет существующие точки данных прямыми линиями. Это выполняется функцией linterp, описанной ниже.
| linterp (vx, vy, x) | Использует векторы данных vx и vy, чтобы возвратить линейно интерполируемое значение y, соответствующее третьему аргументу x. Аргументы vx и vy должны быть векторами одинаковой длины. Вектор vx должен содержать вещественные значения, расположенные в порядке возрастания. |
Эта функция соединяет точки данных отрезками прямых, создавая таким образом ломаную. Интерполируемое значение для конкретного x есть ордината y соответствующей точки ломаной.
Для значений x, расположенных перед первой точкой в vx, Mathcad продолжает ломаную прямой линией, проходящей через первые две точки данных. Для значений x, расположенных за последней точкой в vx, Mathcad продолжает ломаную прямой линией, проходящей через последние две точки данных.
Для получения наилучших результатов значение x должно находиться между самым большим и самым маленьким значениями в векторе vx — маловероятно, что будут полезны значения, вычисленные для x вне этого диапазона. Функция linterp предназначена для интерполяции, а не экстрaполяции. Рисунок 5 показывает некоторые примеры линейной интерполяции.
Рисунок 5: Примеры линейной интерполяции.
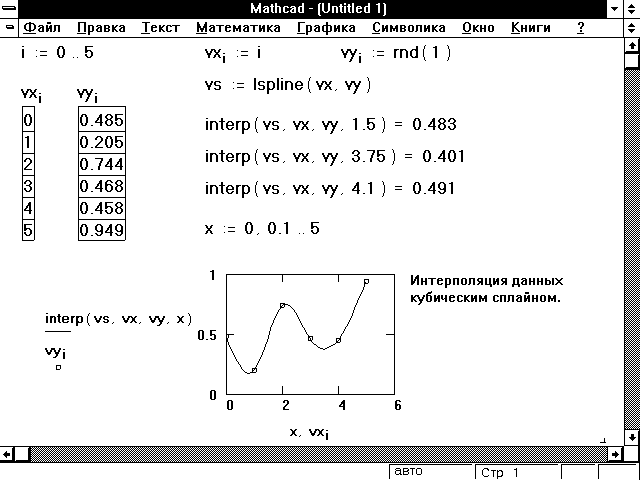
Кубическая сплайн-интерполяция позволяет провести кривую через набор точек таким образом, что первые и вторые производные кривой непрерывны в каждой точке. Эта кривая образуется путем создания ряда кубических полиномов, проходящих через наборы из трёх смежных точек. Кубические полиномы затем состыковываются друг с другом, чтобы образовать одну кривую.
Обратите внимание, что можно сделать то же самое, вычисляя:
Рисунок 6: Пример сплайн-интерполяции.
На практике, возможно, придётся вычислять interp во многих различных точках. Так как обращение к cspline может требовать много времени, и так как возвращаемый ею результат не зависит от рассматриваемой точки, имеет смысл сделать это один раз, сохранить результат и многократно использовать, как описано выше.
Рисунок 6 показывает, как построить сплайн для примера, приведенного на Рисунке 5. Описание шагов, сделанных на Рисунке 6:
Выражение с функцией cspline вычисляет массив вторых производных vs для сплайна, используемого для интерполяции данных из vx и vy.
Как только массив vs найден, функция interp вычисляет интерполируемые значения.
Обратите внимание, что массив vs должен вычисляться только один раз, даже для множественных интерполяций. Так как вычисление vs требует много времени, лучше сохранять промежуточные результаты в виде вектора, чем повторно вычислять их по мере необходимости.
В дополнение к cspline Mathcad поставляется с двумя другими кубическими сплайн-функциями. Три сплайн-функции:
| cspline(vx, vy) pspline(vx, vy) lspline(vx, vy) | Они все возвращают вектор коэффициентов вторых производных, который мы будем называть vs. Этот вектор, vs, обычно используется в функции interp, описанной ниже. Аргументы vx и vy должны быть вещественнозначными векторами одинаковой длины. Значения в vx должны быть вещественны и расположены в порядке возрастания. |
Они все возвращают вектор коэффициентов вторых производных, который мы будем называть vs. Этот вектор, vs, обычно используется в функции interp, описанной ниже. Аргументы vx и vy должны быть вещественнозначными векторами одинаковой длины. Значения в vx должны быть вещественны и расположены в порядке возрастания.
| interp (vs, vx, vy, x) | Возвращает интерполируемое значение y, соответствующее аргументу x. Вектор vs вычисляется на основе векторов данных vx и vy одной из функций lspline, pspline или cspline. |
Интерполируемое значение для конкретного x есть ордината y соответствующей точки сплайна. Для значений x, расположенных перед первой точкой в vx, Mathcad продолжает сплайн первой из составляющих его кубических парабол. Для значений x, расположенных за последней точкой в vx, Mathcad продолжает сплайн последней из составляющих его кубических парабол.
Для получения наилучших результатов значение x должно находиться между самым большим и самым маленьким значениями в векторе vx — маловероятно, что будут полезны значения, вычисленные для x вне этого диапазона. Сплайны предназначены для интерполяции, а не экстрaполяции.
Интерполяция вектора точек
Можно использовать оператор векторизации, чтобы вычислить сразу целый набор интерполируемых значений, соответствующих вектору заданных точек. Это возможно и с interp, и с linterp.
Рисунок 7 показывает, как выполнить эту операцию. Чтобы применить оператор векторизации к функции, щёлкните мышью на имени функции и нажимайте [ ], пока в рамку не попадёт нужная функция. Затем нажмите [Ctrl]- (держите нажатой клавишу [Ctrl] и нажмите знак минус).
Рисунок 7: Вычисление интерполируемых значений в наборе точек.
Интерполяция сплайнами функций нескольких переменных
Mathcad выполняет интерполяцию кубическими сплайнами функции двух переменных тем же самым образом, как и в одномерном случае, обсужденном ранее. Mathcad проводит через сетку узлов поверхность, составленную из кубических полиномов от x и y, таким образом, что первые и вторые частные производные являются непрерывными в каждом узле сетки.
interp( cspline( Mxy, Mz), Mxy, Mz, 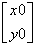
На практике, возможно, придётся вычислять interp во многих различных точках. Так как обращение к cspline может требовать много времени, и так как возвращаемый ею результат не зависит от рассматриваемой точки, имеет смысл сделать это один раз, сохранить результат и многократно использовать, как описано выше.
В дополнение к cspline Mathcad поставляется с двумя другими функциями сплайн-интерполяции. Функции сплайн-интерполяции Mathcad:
| interp (vs, Mxy, Mz, v) | Возвращает интерполируемое значение z, соответствующее точкам x = v0 и y = v1. Вектор vs вычисляется lspline, pspline, или cspline на основе данных из Mxy и Mz. |
Для получения наилучших результатов не используйте функцию interp для значений x и y, удалённых от узлов сетки. Сплайны предназначены для интерполяции, а не экстрaполяции, поэтому маловероятно, что значения, вычисленные для таких x и y, будут полезны.
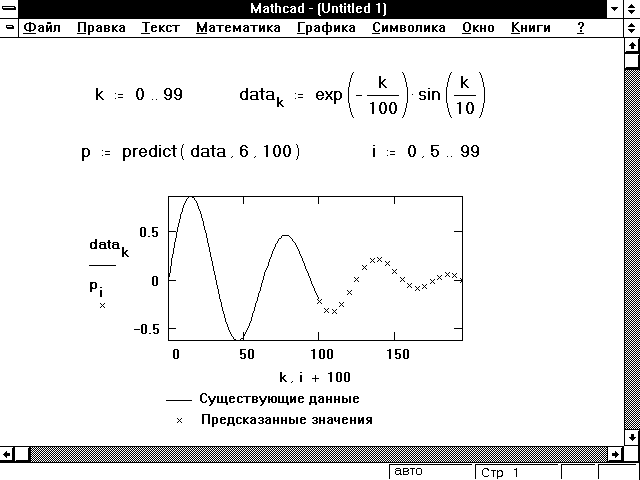
Функции интерполяции, описанные в этом разделе до сих пор, позволяют по заданным значениям некоторой функции в ряде точек оценить её значения в промежуточных точках. Иногда необходимо оценить значения функции в точках, находящихся вне области расположения сетки, на которой заданы значения функции. В Mathcad есть функция predict, которая позволяет это сделать. Эта функция использует линейный алгоритм предсказания, который является полезным, когда экстраполируемая функция является гладкой и осциллирующей, хотя не обязательно периодической. Линейное предсказание можно рассматривать как разновидность экстрaполяции, но его нельзя путать с линейной или полиномиальной экстрaполяцией.
Рисунок 8: Использование функции предсказания для экстраполяции данных.
| Е predict (v, m, n) | Возвращает n предсказанных значений, основанных на m последовательных значениях вектора данных v. Элементы в v должны представлять собой значения, взятые через равные интервалы. |
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter