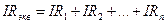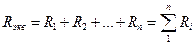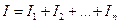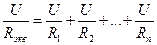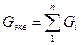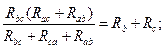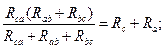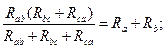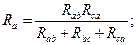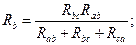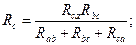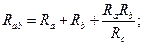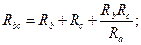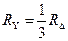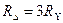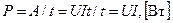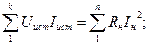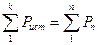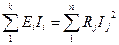Как сделать схему замещения

13.01.202313.02.2023 admin 0 Comments

СОСТАВЛЕНИЕ СХЕМ ЗАМЕЩЕНИЯ

Лекция 3

Составление схем замещения сводится к приведению параметров элементов и ЭДС различных ступеней трансформации к какой-либо одной ступени, выбранной за основную. Параметры элементов и ЭДС выражают в именованных или в относительных единицах. Для определения токов и напряжений в месте КЗ необходимо полную схему замещения преобразовать путем эквивалентирования ветвей к простейшей радиальной ветви согласно рис.1. Тогда начальный ток I_по*, о.е., в месте КЗ равен I_по* = ,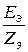

Как сделать схему замещения. Смотреть фото Как сделать схему замещения. Смотреть картинку Как сделать схему замещения. Картинка про Как сделать схему замещения. Фото Как сделать схему замещения

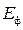
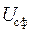
Схема замещения трехфазной электрической системы составляется на одну фазу, соответственно источник питания представляется в ней фазной ЭДС или фазным напряжением , приложенным за сопротивлением энергосистемы: Х_{с макс} и Х_{с мин}.

Дополнительные трудности при расчетах токов КЗ возникают, если в схеме имеется несколько магнитно-связанных цепей, т.е. трансформаторов (автотрансформаторов). В этом случае для упрощения проводимых расчетов такую схему целесообразно представить схемой замещения, заменив имеющиеся в ней магнитно-связанные цепи одной эквивалентной электрически связанной цепью. Составление такой схемы замещения сводится к приведению параметов элементов и ЭДС различных ступеней заданной схемы к одной ступени, выбранной за основную, – той, где установлены устройства релейной защиты, для которых выполняются расчеты. На расчетной схеме и схеме замещения целесообразно обозначить места установки релейной защиты. При этом используют известные соотношения для ЭДС напряжений, токов и сопротивлений при приведении их с одной стороны трансформатора на другую. Общие выражения для определения приведенных к основной ступени значений отдельных величин электрической цепи при наличии n трансформаторов между приводимой и основной ступенью таковы [2]:

для ЭДС 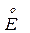= (К_т1∙ К_т2 ∙ … К_т_n)Е;

для напряжения 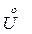= (К_т1∙ К_т2 ∙ … К_т_n)U;

для тока 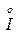= I/(К_т1∙ К_т2 ∙ … К_т_n);

для индуктивного и активного сопротивлений соответственно

= (К_т1∙ К_т2 ∙ … К_т_n) 2 Х;

= (К_т1∙ К_т2 ∙ … К_т_n) 2 R,

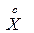
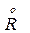
где К_т1, К_т2, …, К_т_n – коэффициенты трансформации силовых трансформаторов (автотрансформаторов).

Таким образом, истинные величины должны быть пересчитаны столько раз, сколько имеется трансформаторов между приводимой цепью и принятой основной ступенью. Для трансформаторов можно принять, что отношение числа витков равно отношению соответствующих напряжений при холостом ходе трансформатора, т.е. К_т = ω₁/ω₂ ≈ U_1хх/U_2хх. Поэтому в вышеприведенных выражениях под коэффициентом трансформации трансформатора (автотрансформатора) понимается отношение междуфазного напряжения холостого хода его обмотки, обращенной в сторону основной ступени напряжения, к аналогичному напряжению его другой обмотки, находящейся ближе к ступени, элементы которой подлежат приведению [2]. Для пояснения данного положения рассмотрим схему на рис. 2.1, где представлена электрическая система, состоящая из генератора Г, трансформаторов Т1 и Т2, линий Л1 и Л2 с тремя ступенями напряжения: первой cтупени (I), второй ступени (II) и третьей ступени (III).

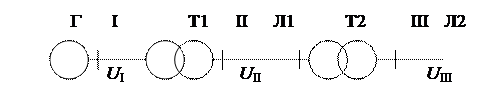Рис. 2. Схема электрической сети с несколькими

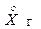
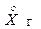
В качестве основной ступени примем третью ступень напряжения – III. Приведенное к III (основной) ступени напряжения, сопротивление генератора Г , Ом, определяется как

= Х_г (U_II/U_I) 2 (U_III/U′_II) 2 ;

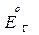
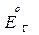
ЭДС генератора , кВ, определяется по выражению

= Е_г (U_II/U_I) (U_III/U′_II) ;

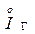
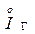
Ток генератора , кА, определяется по выражению

= I_г /(U_II/U_I) (U_III/U′_II),

где К_т1 = U_II/U_I – действительный коэффициент трансформации трансформатора Т1; К_т2 = U_III/U′_II – действительный коэффициент трансформации трансформатора Т2.

Рассмотренное приведение по действительным коэффициентам трансформации называют точным приведением.

В паспортных данных генератора его сопротивление представляют в относительных единицах (о.е.) при номинальных условиях: Х_*г(н). Для нахождения его сопротивления Х_г Ом, можно воспользоваться выражением [2]

где U_н – номинальное напряжение генератора, кВ; I_н – номинальный ток генератора, кА; S_н – номинальная мощность генератора, МВ∙А.

Данное выражение можно использовать для определения сопротивления в именованных единицах и для других элементов электрической системы, у которых параметры даны в относительных единицах, приведенных к номинальным данным этих элементов, т.е.

В паспортных данных трансформатора (автотрансформатора) представлено значение напряжения короткого замыкания в процентах, по нему определяется сопротивление в относительных единицах: Z_т = U_к/100. В большинстве случаев активным сопротивлением трансформатора R_т пренебрегают, а индуктивное сопротивление Х_т принимают равным напряжению короткого замыкания U_к: Х_т = U_к, %.

Как известно, на трансформаторах распределительных сетей 35 кВ и выше устанавливаются автоматические регуляторы напряжения (АРН) для поддержания на шинах низшего напряжения (НН) номинального напряжения при эксплуатационных изменениях режима. Это достигается регулированием коэффициента трансформации с помощью изменения положения регулировочного ответвления трансформатора, чаще всего со стороны ВН трансформатора.

Ниже рассмотрены особенности расчетов токов КЗ в сетях, содержащих трансформаторные цепи со встроенными устройствами регулирования напряжения под нагрузкой РПН.

Для двухобмоточного трансформатора (рис. 3), в котором предусматривается регулирование с помощью ответвлений со стороны нейтралей от обмотки высшего напряжения ВН (I), отношение напряжения на обмотках при холостом ходе равно отношению количества витков:

где ω_1ном – число витков обмотки ВН трансформатора в номинальном режиме; ± ∆ω – число витков ответвлений от этой обмотки (ступеней) для положительного и отрицательного регулирования напряжения (принимаются одинаковыми); ω_II – число витков обмотки низшего напряжения НН, U_I – напряжение обмотки ВН, U_II – напряжение обмотки НН.

Используя отношения напряжений к их номинальным значениям, формулу (2.14) можно привести к виду

Из последних выражений видно, что при работе трансформатора в понижающем режиме (рис. 3) при увеличении или уменьшении числа витков обмотки ВН (I) напряжение на обмотке НН (II) изменяется в обратном направлении.

Рис.3. Принципиальная схема регулирования напряжения

Из представленных выражений видно, что при работе трехобмоточного трансформатора в понижающем режиме одновременно и пропорционально изменяются среднее и низшее напряжения.

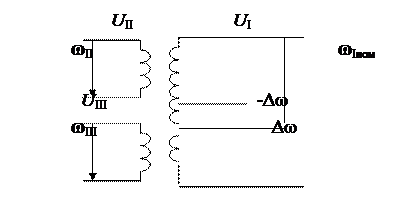Рис. 4. Принципиальная схема регулирования

напряжения трехобмоточного трансформатора

При этом увеличение или уменьшение числа витков обмотки ВН вызывает изменение напряжения обмоток СН и НН в обратном направлении.

Сопротивление трансформатора Z_т, Ом, приведенное к напряжению одной из сторон трансформаторной цепи, где предусматривается регулирование, равно [2]

где S_{т ном} – номинальная мощность трансформатора, МВ·А; U_рег – напряже-ние холостого хода на соответствующей стороне трансформаторной цепи, кВ; U_к – напряжение короткого замыкания, %.

Дата добавления: 2014-01-07 ; Просмотров: 3364 ; Нарушение авторских прав?

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Лекция №2. 1. Схемы замещения электрических цепей

1. Схемы замещения электрических цепей

2. Эквивалентные преобразования пассивных электрических цепей

3. Расчет цепей посредством двух законов Кирхгофа

4. Мощность в цепях постоянного тока

5. Баланс мощностей

1. Схемы замещения электрических цепей

Схемой электрической цепи называется ее графическое изображение с использованием обозначений идеальных элементов. Например:

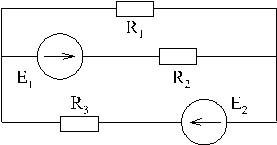Если учесть сопротивление утечки реального конденсатора, сопротивление витков реальной индуктивной катушки и внутреннее сопротивление реального источника ЭДС, то можно составить соответствующие схемы замещения этих элементов:

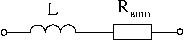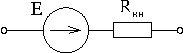Отсюда следует, что все схемы по сути дела являются лишь более или менее точными схемами замещения реальных электрических цепей.

Представленный на рис.2 контур содержит три участка: участок с постоянным напряжением U = Е, не зависящим от тока источника, и участки с напряжениями RвхI и U на нагрузке Rн.

Направление ЭДС выбрано совпадающим с направлением тока, но оно противоположно напряжению на этом элементе.

2. Эквивалентные преобразования пассивных электрических цепей

Для упрощения анализа сложных электрических цепей отдельные их участки, не содержащие ЭДС, или пассивные цепи целиком можно заменить одним эквивалентным сопротивлением. Под эквивалентным понимают такое сопротивление, которое, будучи включенным в цепь вместо заменяемой группы сопротивлений, не изменяет распределение токов и напряжений в остальной части цепи.

При последовательном соединении сопротивлений по каждому из них

протекает один тот же ток, следовательно, падение напряжения на эквивалентном сопротивлении должно быть равно сумме падений напряжений на исходных сопротивлениях:

Если группа заменяемых сопротивлений соединена параллельно, то

напряжения на каждом из них и на эквивалентном сопротивлении одинаковы. Условия эквивалентности будут выполнены, если ток через искомое сопротивление будет равен сумме токов через отдельные параллельные сопротивления:

Используя закон Ома для отдельного сопротивления, можем записать:

Поскольку величина, обратная сопротивлению, есть проводимость, то, вводя обозначения для проводимости 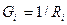, получим:

При анализе сложных схем встречаются случаи, когда часть схемы образует так называемый треугольник сопротивлений:

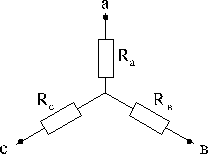Схема упрощается, если треугольник с сопротивлениями Rав, Rвс, Rса заменить эквивалентной звездой с сопротивлениями Rа, Rв, Rс. Иногда, наоборот, необходимо обратное преобразование звезды в треугольник. Схемы треугольника и звезды считаются эквивалентными, если после преобразования все токи и напряжения в остальных частях схемы (не затронутых преобразованиями) остаются неизменными.

Очевидно, условия эквивалентности должны выполняться и при обрыве проводов, подходящих к узлам «а», «в», «с». Например, при обрыве провода, подходящего к узлу «а», сопротивления между точками «в» и «с» в треугольнике и звезде должны быть одинаковы, т.е.:

Рассуждая аналогичным образом, можно записать:

Решая полученную систему уравнений относительно Rа, Rв и Rс, получим формулы эквивалентного преобразования треугольника в звезду:

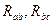
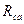
Решая систему относительно и получим формулы преобразования звезды в треугольник:

В частном случае, когда сопротивления звезды или треугольника одинаковы, эти формулы упрощаются:

3. Расчет цепей посредством двух законов Кирхгофа

а) произвольно задаются положительными направлениями токов во всех ветвях схемы,

б) для всех узлов схемы кроме одного составляются уравнения по 1-му закону Кирхгофа,

в) для всех независимых контуров составляются уравнения по 2-му закону Кирхгофа (контур будет считаться независимым от остальных, если в него входит хотя бы одна новая ветвь, т.е. не вошедшая в состав других контуров).

Общее число уравнений, составленных по 1 и 2-му законам Кирхгофа должно быть равно числу неизвестных токов. Полученная система линейных уравнений разрешается относительно токов с использованием известных методов решения систем уравнений (например, с помощью определителей)

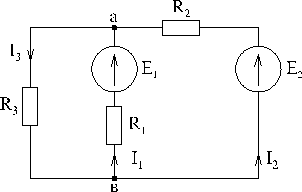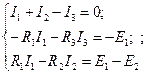Если при решении системы уравнений значение какого-либо тока получилось отрицательным, то это означает, что истинное направление тока противоположно выбранному. Данный метод расчета является универсальным, однако расчет вручную возможен лишь для несложных схем (4-5 неизвестных тока). Для более сложных схем требуется применение иных методов или вычислительной техники.

4. Мощность в цепях постоянного тока

Для оценки энергетических условий важно знать сколь быстро совершается работа.

Отношение работы «А» к соответствующему промежутку времени t определяет мощность: