Как сделать задачу на построение

Класс: 7

Презентация к уроку

Цели уроков:

Тип уроков: урок ознакомления с новым материалом, урок отработки практических навыков, урок закрепления навыков и умений.

2. План решения задач на построение;

3. Выполнение простейших задачи на построение;

4. Решение задач на построение;

5. Примеры задач на построение

1. Вступительная лекция (слайд 3):

Зачем Евклиду потребовались построения? Зачем вообще в геометрии построения? Зачем нужно учиться решать задачи на построение (Евклид называл их проблемами, в отличие от теорем)?

Решение задач на построение развивает геометрическое мышление гораздо полнее и острее, чем решение задач на вычисление, и способно вызвать увлечение работой, которое приводит к усилению любознательности и к желанию расширить и углубить изучение геометрии.

Инструменты для построения: (слайд 4):

Инструменты, употребляемые для выполнения геометрических построений, весьма разнообразны. К основным инструментам принадлежат линейка и циркуль, служащие для проведения прямых линий, одиночных, параллельных и перпендикулярных, и окружностей. Угольник есть вспомогательный инструмент, так как, имея линейку и циркуль, можно строить параллельные и перпендикулярные прямые. К вспомогательным инструментам относится также миллиметровая шкала, которую можно построить с помощью циркуля и линейки, отложив на прямой линии циркулем одинаковые сантиметровые отрезки и разделив каждый из этих отрезков на 10 равных между собою частей. Транспортир есть уже самодеятельный инструмент, так как точное в геометрическом смысле градуирование любой дуги на произвольное число равных частей с помощью линейки и циркуля невозможно.

С глубокой древности повелось допускать к исполнению геометрических построений только циркуль и линейку, т. е. приборы, позволяющие проводить прямые линии и окружности.

С помощью циркуля можно провести произвольную окружность, можно провести окружность с данным центром и данного радиуса. Можно также на данной прямой отложить отрезок, равный данному.

2. План решения задач на построение (слайд 5)

Выполнив анализ, наметив план, описывают само построение. Оно может содержать лишь основные построения и элементарные действия с циркулем и линейкой.

Далее требуется привести доказательство того, что построенная фигура удовлетворяет всем условиям задачи и, кроме того, проделать исследование, т.е. выяснить, всегда ли (при любых ли данных) описанное построение возможно, нет ли частных случаев, в которых построение упрощается или делается невозможным.

Таким образом, решение задачи на построение состоит из 4-х частей: анализ, построение, доказательство, исследование. Анализ опускается в простых задачах или в тех, решение которых уже известно.

3. Выполнение простейших задачи на построение

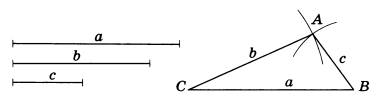
Построение 1: построить треугольник по трем сторонам, т.е. построить треугольник, стороны которого равны трем данным отрезкам а, b и с. Построение треугольника по трем сторонам сводится к построению последовательно трех отрезков, равных данным (слайд 6).

Доказательство следует непосредственно из равенства сторон построенного треугольника заданным отрезкам.

Построение 2: построить угол, равный данному, от данной полупрямой в данную полуплоскость (слайды 7-8).

Построение 3: построить биссектрису данного угла (слайды 9-10).

Построение 4: деление отрезка пополам (одновременное построение серединного перпендикуляра данного отрезка) (слайд 11).

Построение 5: через точку O провести прямую, перпендикулярную данной прямой a. Рассмотреть два возможных случая (слайды 12-14).

Построение 6: построение прямой, проходящей через данную точку А параллельно данной прямой а. (слайд 15).

4. Решение задач на построение;

Задача 1. Построить равнобедренный треугольник по углу при основании и высоте, опущенной на основание (слайд 16).

Анализ. ( рис. 1) Предположим, что задача решена, и построен равнобедренный треугольник АВС, АВ = ВС, в котором угол ВАС = a и высота BD = отрезку h.

Через точку А проводим прямую, перпендикулярную прямой AN (построение 5), и на построенной прямой откладываем отрезок АМ = h (в той же полуплоскости, в которой построен угол).

Через точку М проводим прямую, параллельную прямой AN (построение 6), точку ее пересечения со стороной угла обозначаем В.

Из точки В опускаем перпендикуляр BD на прямую AN (построение 5) и откладываем DC = DA. Соединяем В и С.

Исследование: В равнобедренном треугольнике угол при основании острый, поэтому построение возможно, если заданный угол острый.

Построение единственно, т.к. точка В находится единственным образом. Задача имеет только одно решение.

Задача 2. Построить треугольник по данному периметру и двум углам (слайд 17).

Анализ (рис. 3) Предположим, что такой треугольник АВС построен.

Аналогично 3 = 4 = /2. В треугольнике А₁В₁С известны два угла 1 и 3 и сторона между ними А₁В₁ = Р. Такой треугольник можно построить, тогда точки А и В найдутся, как точки пересечения серединных перпендикуляров отрезков А₁С и В₁С с прямой А₁В₁.

Доказательство: По построению А₁D = DC, AD А₁С, следовательно, А₁АD = CAD (по первому признаку) и А₁А = АС.

Исследование: Построение возможно всегда, если только сумма двух углов меньше 180° (сумма двух углов треугольника всегда меньше 180° ). Решение единственно, т.к. точка С, а затем точки А и В определяются единственным образом.

Анализ (рис. 4): Предположим, что построен прямоугольный треугольник АВС с углом А, равным a, и разностью катетов, равной m.

Применим метод спрямления: отложим на прямой АС от точки С отрезок СК, равный ВС, тогда АК = m. В треугольнике АКВ известна сторона АК и два прилежащих угла: ВАК = a и ВКА = 135°. Такой треугольник можно построить, а точку С найти как основание перпендикуляра из точки В на прямую АК.

На прямой l выбираем точку А и откладываем отрезок АК = m. Через точку К проводим перпендикуляр KL к прямой АК (построение 5).

Проводим биссектрису КР угла, дополнительного к прямому углу АКL (построение 3).

От луча АК откладываем угол КАМ, равный данному углу a (построение 2), точку пересечения с прямой КР обозначаем В.

Исследование: Построение возможно, если существует треугольник А₁КС со сторонами А₁С = СК = m и А₁К =а, что возможно лишь при условии а . Построение единственно, все точки определяются единственным образом.

5. Задачи для самостоятельного решения

Задача 1. Через данную точку провести прямую под данным углом к данной прямой (слайд 20).

Указание к решению задачи: Построить угол, равный данному в произвольной точке данной прямой, одна из сторон которого лежит на этой прямой; затем через данную точку провести параллельную прямую.

Задача 2. описать окружность, которая проходила бы через данную точку А и касалась бы данной прямой в данной на ней точке В (слайд 21).

Задача 3. Провести в треугольнике прямую, параллельную основанию так, чтобы отрезок, заключенный между боковыми сторонами был равен сумме отрезков боковых сторон, считая от основания (слайд 22).

Указание к решению задачи (слайд):Через точку пересечения биссектрис провести прямую MN, параллельную основанию. Получим равнобедренные треугольники ONC и ОМА (теорема о накрест лежащих углах при параллельных прямых, свойства сторон и углов в равнобедренном треугольнике).

Задача 4. На прямой АВ найти такую точку С, чтобы лучи СМ и СN, проведенные из С через данные точки М и N, расположенные по одну сторону от АВ, составляли с лучами СА и СВ равные углы (слайд 23).

Источник

Инструменты пользователя

Инструменты сайта

Боковая панель

Геометрия:

Контакты

Основные задачи на построение

В задачах на построение будем рассматривать построение геометрической фигуры, которое можно выполнить с помощью линейки и циркуля.

С помощью линейки можно провести:

С помощью циркуля можно описать из данного центра окружность данного радиуса.

Циркулем можно отложить отрезок на данной прямой от данной точки.

Рассмотрим основные задачи на построение.

Задача 1. Построить треугольник с данными сторонами а, b, с (рис.1).

Решение. С помощью линейки проведем произвольную прямую и возьмем на ней произвольную точку В. Раствором циркуля, равным а, описываем окружность с центром В и радиусом а. Пусть С — точка ее пересечения с прямой. Раствором циркуля, равным с, описываем окружность из центра В, а раствором циркуля, равным b — окружность из центра С. Пусть А — точка пересечения этих окружностей. Треугольник ABC имеет стороны, равные a, b, c.

Замечание. Чтобы три отрезка прямой могли служить сторонами треугольника, необходимо, чтобы больший из них был меньше суммы двух остальных (а

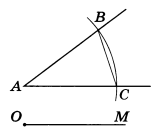
Задача 2. Отложить от данного луча угол, равный данному.

Решение. Данный угол с вершиной А и луч ОМ изображены на рисунке 2.

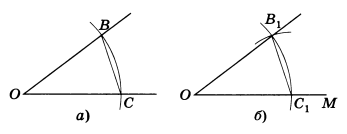
Проведем произвольную окружность с центром в вершине А данного угла. Пусть В и С — точки пересечения окружности со сторонами угла (рис.3, а). Радиусом АВ проведем окружность с центром в точке О — начальной точке данного луча (рис.3, б). Точку пересечения этой окружности с данным лучом обозначим С₁. Опишем окружность с центром С₁ и радиусом ВС. Точка В₁ пересечения двух окружностей лежит на стороне искомого угла. Это следует из равенства Δ ABC = Δ ОВ₁С₁ (третий признак равенства треугольников).

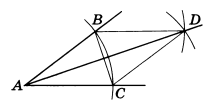
Задача 3. Построить биссектрису данного угла (рис.4).

Решение. Из вершины А данного угла, как из центра, проводим окружность произвольного радиуса. Пусть В и С — точки ее пересечения со сторонами угла. Из точек В и С тем же радиусом описываем окружности. Пусть D — точка их пересечения, отличная от А. Луч AD делит угол А пополам. Это следует из равенства Δ ABD = Δ ACD (третий признак равенства треугольников).

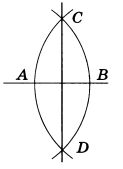
Задача 4. Провести серединный перпендикуляр к данному отрезку (рис.5).

Решение. Произвольным, но одинаковым раствором циркуля ( большим 1/2 АВ ) описываем две дуги с центрами в точках А и В, которые пересекутся между собой в некоторых точках С и D. Прямая CD будет искомым перпендикуляром. Действительно, как видно из построения, каждая из точек С и D одинаково удалена от А и В; следовательно, эти точки должны лежать на серединном перпендикуляре к отрезку АВ.

Задача 5. Разделить данный отрезок пополам. Решается так же, как и задача 4 (см. рис.5).

Задача 6. Через данную точку провести прямую, перпендикулярную данной прямой.

Решение. Возможны два случая:

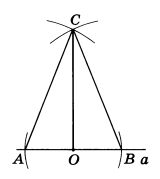
1) данная точка О лежит на данной прямой а (рис. 6).

Из точки О проводим произвольным радиусом окружность. Она пересекает прямую а в двух точках А и В. Из точек А и В проводим окружности радиусом АВ. Пусть С — точка их пересечения. Получаем ОС ⊥ AB. В самом деле, Δ АСВ — равнобедренный, СА = СВ. Отрезок СО есть медиана этого треугольника, а следовательно, и высота;

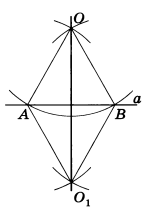
2) данная точка О не лежит на данной прямой а (рис.7).

Из точки О проводим произвольным радиусом окружность, пересекающую прямую а в точках А и В. Из точек А и В тем же радиусом проводим окружности. Пусть О₁ — точка их пересечения, отличная от О. Получаем ОО₁ ⊥ AB. В самом деле, точки О и О₁ равноудалены от концов отрезка АВ и, следовательно, лежат на серединном перпендикуляре к этому отрезку.

Источник

Задачи на построение. 7-й класс, геометрия

Разделы: Математика

Класс: 7

Тема урока: «Задачи на построение».

Сегодня мы будем учиться строить треугольники по трем заданным элементам с помощью циркуля и линейки.

Чтобы построить треугольник, нужно сначала уметь строить отрезок, равный заданному, и угол, равный заданному. Конечно, можно это сделать с помощью линейки с делениями и транспортира, но в математике требуется еще и уметь выполнять построения с помощью циркуля и линейки без делений.

Анализ и исследование задачи необходимы так же, как и само построение. Необходимо посмотреть, в каких случаях задача имеет решение, а в каких – решения нет.

1. Построение отрезка, равного заданному.

2. Строим угол, равный заданному, с помощью циркуля и линейки.

А вот теперь перейдем к построению треугольников по трем элементам.

3. Построение треугольника по двум сторонам и углу между ними.

Дано	Требуется построить	Построение
1. Построить угол А, равный заданному углу. 2. На одной стороне угла отметить точку С так, чтобы отрезок АС был равен заданному отрезку b. 3. На другой стороне угла отметить точку В так, чтобы отрезок АВ был равен заданному отрезку с. 4. Соединить с помощью линейки точки В и С.

Построен треугольник АСВ по двум сторонам и углу между ними.

Самостоятельная работа к схеме 3.

Построить треугольник ВСН, если ВС = 3 см, СН = 4 см, С = 35є.

Построить треугольник СДЕ, у которого ДС = 4 см, ДЕ = 5 см, Д = 110є.

Подсказка. Перед построением треугольника необходимо сделать «от руки» чертеж треугольника, где показаны все заданные элементы.

4. Построение треугольника по стороне и прилежащим к ней углам.

Дано

Требуется построить

Построение

1. Произвольно начертить отрезок АВ, равный заданному отрезку c.
2. Построить угол А, равный заданному.
3. Построить угол В, равный заданному.

Точка пересечения двух сторон углов А и В – вершина треугольника С.

Построили треугольник АСВ по стороне и двум заданным углам.

Самостоятельная работа к схеме 4.

Построить треугольник КМО, если КО = 6 см, К = 130є, О = 20є.

Построить треугольник ВСР, если С = 15є, Д = 50є, СД = 3 см.

5. Построение треугольника по трем сторонам.

Дано

Требуется построить

Построение

1. Построить отрезок АВ, равный заданному отрезку c.
2. Из точки А провести часть окружности, радиус которой
равен заданному отрезку b.
3. Из точки В провести часть окружности, радиус которой
равен заданному отрезку a, обе окружности пересекаются в точке С.

Построили треугольник АСВ по трем сторонам.

Самостоятельная работа к схеме 5.

Построить треугольник ОДЕ, если ОД = 4 см, ДЕ = 2 см, ЕО = 3 см.

Построить треугольник МНО, если МН = 1 см, НО = 4 см, ОМ = 3 см.

После построения любого треугольника, самостоятельно провести доказательство того, что получившийся треугольник – искомый, и по возможности провести исследование.

Источник