Как сделать задачу по статистике

Как сделать задачу по статистике

Теория по решению задачи.

Статистическая сводка – научно обработанный материал статистического наблюдения в целях получения обобщенной характеристики изучаемого явления.

Группировка – распределение единиц изучаемого объекта на однородные типичные группы по существенным для них признакам.

Интервал – разница между максимальным и минимальным значением признака в каждой группе.

, где

i – величина интервала;

R – размах колебания (R=xmax-xmin)

n – принятое число групп;

xmax, xmin – наибольшее и наименьшее значение признака в изучаемой совокупности.

, где

N – число наблюдений

Типовая задача № 1

Распределите потребительские общества по размеру товарооборота на 3 группы с равными интервалами. В каждой группе подсчитайте количество потребительских обществ, сумму товарооборота, сумму издержек обращения. Результаты группировок представьте в табличной форме. К какому виду статистических таблиц относится составление вами таблица, и какой вид группировки она содержит?

Имеются основные экономические показатели потребительских обществ за отчетный период:

Товарооборот в млн. грн.

Издержки обращения, в млн. грн.

Ход решения задачи:

Т. к. нам известен группировочный признак, работу необходимо начать в определения величины интервала по формуле:

Образец 3 группы потребительских обществ по размеру товарооборота.

Определяем границы групп:

1 группа: 180+90=270 (180-270)

2 группа: 270+90=360 (270-360)

3 группа: 360+90+450 (360-450)

После того, как выбран группировочный признак, намечено число групп и образованы сами группы, необходимо отобрать показатели, которыми будут характеризоваться группы, и определить их величину по каждой группе.

В нашем примере каждую группу необходимо охарактеризовать следующими показателями:

а) количеством потребительских обществ;

б) суммой товарооборота;

в) суммой издержек обращения.

Для заполнения итоговой таблицы составим предварительно рабочие таблицы № 2, 3, 4.

Группа потребительских обществ с товарооборотом от 180 до 270 млн. грн.

Номер потребительского общества

Товарооборот, в млн. грн.

Сумма издержек обращения, в млн. грн.

Группа потребительских обществ с товарооборотом от 270 до 3660 млн. грн.

Номер потребительского общества

Товарооборот, в млн. грн.

Сумма издержек обращения, в млн. грн.

Группа потребительских обществ с товарооборотом от 360 до 450 млн. грн.

Номер потребительского общества

Товарооборот, в млн. грн.

Сумма издержек обращения, в млн. грн.

Итоговые показатели рабочих таблиц занесем в окончательную итоговую таблицу и получим групповую таблицу № 5.

Группировка потребительских обществ, по размеру товарооборота:

Группы потребительских обществ по размеру товарооборота, млн. грн.

Количество потребительских обществ

Товарооборот, в млн. грн.

Сумма издержек обращения, в млн. грн.

Вывод: По результатам итоговой таблицы можно сделать вывод, что с увеличением объема товарооборота потребительских обществ, относительный показатель уровня издержек обращения снижается. Следовательно, между ними существует обратная связь. Составленная нами таблица является групповой таблицей, т. к. ее подлежащее содержит группы потребительских обществ по размеру товарооборота. Она содержит аналитический вид группировки.

Теория по решению задачи.

Статистический ряд распределения – упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.

Дискретный вариационный ряд – характеризует распределение единиц совокупности по дискретному (прерывному) признаку.

Интервальный вариационный ряд – характеризует распределение единиц совокупности по интервальному (непрерывному) признаку.

Для изображения дискретных вариационных рядов распределения используется «полигон распределения». Для графического изображения интервального вариационного ряда применяются «гистограмма» и «кумулята».

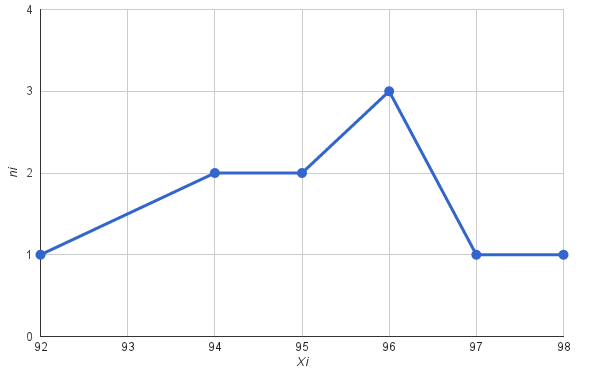
Задача 1.

На экзамене по истории студенты получили оценки:

Построить дискретный вариационный ряд распределения студентов по баллам и изобразить его графически.

Ход решения задачи:

Определяем элементы ряда распределения: варианты, частоты, частоты.

Кол-во студентов с такой оценкой, человек

В процентах к итогу

Теперь графически изобразим дискретный ряд распределения в виде помпона распределения.

Можно сделать вывод о том, что преобладающее большинство студентов получило «4» (43,3 %).

Задача 2.

Во время выборочной проверки было установлено, что продолжительность одной покупки в кондитерском отделе магазина была такой: (секунды).

Построить интервальный вариационный ряд распределения покупок по продолжительности, создав 4 группы с одинаковыми интервалами. Обозначить элементы ряда. Изобразить его графически, сделать вывод.

Ход решения задачи по статистике:

Определяем элементы ряда распределения: варианты, частоты, частости, накопленные частоты.

Но прежде рассчитаем границы 4 заданных групп с одинаковыми интервалами:

Величину интервала определим по формуле .

В нашем случае

Границы групп соответственно равны:

Группы покупок по продолжительности, сек.

В процентах к итогу

Накопленные частоты

Теперь графически отобразим наш интервальный вариационный ряд в виде гистограммы и кумуляты.

По таблице и графика можно сделать вывод о том, что преобладающее большинство покупок (16 или 53.3%) находится во временном интервале 75-82, сек.

Теория по решению статистической задачи.

Абсолютные величины – показатели, которые выражают размеры общественных явлений и процессов числом единиц совокупности.

Относительные величины – показатели, выражающие количественные соотношения численностей или величин признаков изучаемых явлений.

Виды относительных величин:

1) Относительная величина выполнения плана:

2) Относительная величина планового задания:

3) Относительная величина динамики:

4) Относительная величина структуры:

5) Относительная величина сравнения отражает соотношение двух объемов или уровней в пространстве: соотношение производства автомобилей в Украине и России, соотношение уровней оплаты труда в разных хозяйствах, соотношение уровней производительности на разных предприятиях отрасли и т. д.

6) Относительная величина координации получается посредством деления друг на друга разноименных исходных показателей, она дает типичную характеристику соотношения одно-порядковых по значимости исходных показателей, во-первых, непосредственно связанных между собой, во-вторых, обладающих некоторой общностью.

7) Относительная величина интенсивности:

Типовая задача № 1

Два консервных завода выработали по 100 тыс. шт. банок виноградного сока. На первом заводе емкость каждой банки составляет 500 см3, а на втором – 200 см3. Можно ли сказать, что оба завода работали одинаково?

Ход решения задачи по статистике:

Для того, чтобы ответить на этот вопрос необходимо установить коэффициенты перевода фактического объема банок в условные банки и затем умножить количество выпущенных банок на эти коэффициенты. Представим расчет в таблице № 1.

Количество выпущенных банок, тыс. шт.

Коэффициенты перевода

Количество выпущенных условных банок, тыс. шт.

Таким образом, завод № 1 по сравнению с заводом № 2 выпустил виноградного сока на 84,8 тыс. Банок больше (141,4-56,6).

Имеются следующие данные розничного товарооборота:

Розничный товарооборот (млн. грн.)

Фактически за базисный год

1. Относительную величину выполнения плана.

2. Относительную величину планового задания.

3. Относительную величину динамики.

Ход решения задачи:

1. Определяем относительную величину выполнения плана по двум универмагам:

2. Определим относительную величину планового задания:

3. Определяем относительную величину динамики:

Теория по решению статистической задачи:

Средние величины – это показатели. Выражающие типичные черты и дают обобщающую количественную характеристику уровня признака по совокупности однородных явлений.

1. Средняя арифметическая:

2. Средняя гармоническая:

3. Средняя квадратическая:

4. Средняя хронологическая:

5. Средняя геометрическая:

К1, К2, К3 и Кn – коэффициенты динамики по отношению к предыдущему периоду.

6. мода интервальных рядов распределения вычисляется по следующей формуле:

х0 – минимальная граница модального интервала;

i – величина интервала;

f2 – частота модального интервала;

f1 – частота интервала, предшествующего модальному;

f3 – частота интервала, следующего за модальным.

Мода для дискретных рядов распределения – это наиболее часто встречающаяся величина признака в данной совокупности.

7. Медиана для интервальных рядов распределения вычисляется по формуле:

x0 – нижняя граница медианного интервала;

i – величина медианного интервала;

∑f – сумма частот ряда;

SМЕ-1 – сумма накопленных частот, предшествующих медианному интервалу;

fМЕ – частота медианного интервала.

Чтобы определить медиану в дискретном вариационном ряду. Необходимо сумму частот разделить пополам и к полученному результату добавить ½.

Типовая задача № 1

Имеются следующие данные о заработной плате рабочих:

Источник

Решение задач по математической статистике

УЗНАТЬ СТОИМОСТЬ РАБОТЫ
В рамках образовательной программы вуза вряд ли встретишь отдельную дисциплину с названием «математическая статистика», однако элементы математической статистики часто изучаются в совокупности с теорией вероятностей, но только после изучения основного курса теории вероятностей.

Математическая статистика: общие сведения

Математическая статистика – это раздел математики, который разрабатывает методы регистрации, описания и анализа данных каких-либо наблюдений и экспериментов, целью которых является построение вероятностных моделей массовых случайных явлений.

Математическая статистика как наука возникла в XVII в. и развивалась параллельным курсом с теорией вероятностей. Большой вклад в развитие науки внесли в XIX-XX вв. Чебышев П.Л., Гаусс К., Колмогоров А.Н. и др.

Общая задача математической статистики заключается в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Основными разделами математической статистики являются:

К наиболее распространенным задачам математической статистики, которые изучаются в вузе и часто встречаются на практике, относятся:

Задачи определения оценок параметров выборки

Изучение математической статистики начинается с определения таких понятий как «выборка», «частота», «относительная частота», «эмпирическая функция», «полигон», «кумулята», «гистограмма» и т.д. Далее идет изучение понятий оценок (смещенная и несмещенная): выборочная средняя, дисперсия, исправленная дисперсия и т.д.

Рассмотрим простейшую задачу данного типа.

Задача

Измерение роста детей младшей группы детского сада представлено выборкой:
92, 96, 95, 96, 94, 97, 98, 94, 95, 96.
Найдем некоторые характеристики этой выборки.

Решение

Размер выборки (число измерений; N): 10.
Наименьшее значение выборки: 92. Наибольшее значение выборки: 98.
Размах выборки: 98 – 92 = 6.
Запишем ранжированный ряд (варианты в порядке возрастания):
92, 94, 94, 95, 95, 96, 96, 96, 97, 98.
Сгруппируем ряд и запишем в таблицу (каждой варианте поставим в соответствие число ее появлений):

Вычислим относительные частоты и накопленные частоты, результат запишем в таблицу:

xi	92	94	95	96	97	98	Итого
ni	1	2	2	3	1	1	10
	0,1	0,2	0,2	0,3	0,1	0,1	1
Накопленные частоты	1	3	5	8	1	10

Построим полигон частот выборки (отметим на графике варианты по оси ОХ, частоты по оси OY, соединим точки линией).

Выборочную среднюю и дисперсию вычислим по формулам (соответственно):

Можно находить и другие характеристики выборки, но для общего представления вполне достаточно найденных характеристик.

Задачи на проверку статистических гипотез

Задачи, относящиеся к данному типу, сложнее задач предыдущего типа и их решение зачастую более объемно и трудоемко. Прежде чем приступать к решению задач, сначала изучаются понятия статистической гипотезы, нулевой и конкурирующей гипотезы и т.д.

Рассмотрим простейшую задачу данного типа.

Задача

Даны две независимые выборки объема 11 и 14, извлеченные из нормальных совокупностей X, Y. Известны также исправленные дисперсии, равные соответственно 0,75 и 0,4. Необходимо проверить нулевую гипотезу о равенстве генеральных дисперсий при уровне значимости γ=0,05. Конкурирующую гипотезу выбрать по желанию.

Решение

Нулевая гипотеза для нашей задачи записывается следующим образом:

В качестве конкурирующей гипотезы рассмотрим следующую:

Вычислим отношение большей исправленной дисперсии к меньшей и получим наблюдаемое значение критерия:

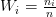
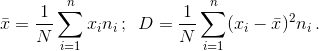
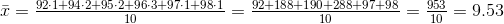
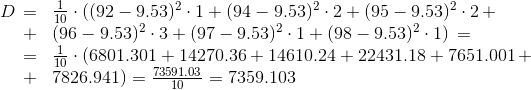
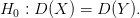
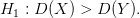
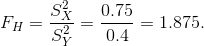
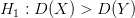Так как конкурирующая гипотеза, которую мы выбрали, имеет вид , то критическая область является правосторонней.
По таблице для уровня значимости 0,05 и числам степеней свободы равным 10 (11 – 1 = 10) и 13 (14 – 1 = 13) соответственно найдем критическую точку:

Так как наблюдаемое значение критерия меньше критического значения (1,875

Источник