Как сделать задачу таблицей
Как в Excel создаются формулы и таблицы. Пошагово
Работа в Excel c формулами и таблицами для чайников. Как же делать формулы и таблицы?
Формула предписывает программе Excel порядок действий с числами, значениями в ячейке или группе ячеек. Без формул электронные таблицы не нужны в принципе. Формулы и таблицы
Excel это очень важный момент!
Конструкция формулы включает в себя: константы, операторы, ссылки, функции, имена диапазонов, круглые скобки содержащие аргументы и другие формулы. На примере разберем практическое применение формул для начинающих пользователей.
ФОРМУЛЫ В EXCEL ДЛЯ ЧАЙНИКОВ
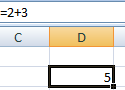
Чтобы задать формулу для ячейки, необходимо активизировать ее (поставить курсор) и ввести равно (=). Так же можно вводить знак равенства в строку формул. После введения формулы нажать Enter. В ячейке появится результат вычислений.
В Excel применяются стандартные математические операторы:
| Оператор | Операция | Пример |
| + (плюс) | Сложение | =В4+7 |
| — (минус) | Вычитание | =А9-100 |
| * (звездочка) | Умножение | =А3*2 |
| / (наклонная черта) | Деление | =А7/А8 |
| ^ (циркумфлекс) | Степень | =6^2 |
| = (знак равенства) | Равно | |
| Больше | ||
| = | Больше или равно | |
| <> | Не равно |
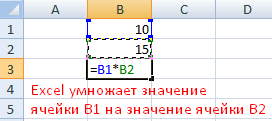
Символ «*» используется обязательно при умножении. Опускать его, как принято во время письменных арифметических вычислений, недопустимо. То есть запись (2+3)5 Excel не поймет.
Программу Excel можно использовать как калькулятор. То есть вводить в формулу числа и операторы математических вычислений и сразу получать результат.
Но чаще вводятся адреса ячеек. То есть пользователь вводит ссылку на ячейку, со значением которой будет оперировать формула.
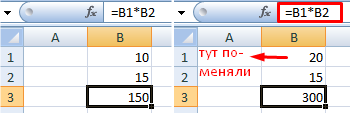
При изменении значений в ячейках формула автоматически пересчитывает результат.
Ссылки можно комбинировать в рамках одной формулы с простыми числами.
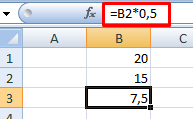
Оператор умножил значение ячейки В2 на 0,5. Чтобы ввести в формулу ссылку на ячейку, достаточно щелкнуть по этой ячейке.
Если в одной формуле применяется несколько операторов, то программа обработает их в следующей последовательности:
Поменять последовательность можно посредством круглых скобок: Excel в первую очередь вычисляет значение выражения в скобках.
КАК В ФОРМУЛЕ EXCEL ОБОЗНАЧИТЬ ПОСТОЯННУЮ ЯЧЕЙКУ
Различают два вида ссылок на ячейки: относительные и абсолютные. При копировании формулы эти ссылки ведут себя по-разному: относительные изменяются, абсолютные остаются постоянными.
Все ссылки на ячейки программа считает относительными, если пользователем не задано другое условие. С помощью относительных ссылок можно размножить одну и ту же формулу на несколько строк или столбцов.
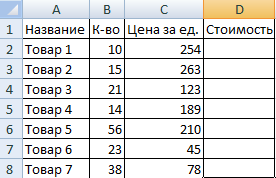
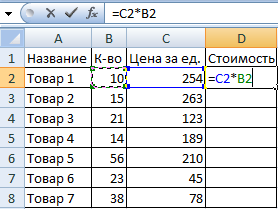
2. Вспомним из математики: чтобы найти стоимость нескольких единиц товара, нужно цену за 1 единицу умножить на количество. Для вычисления стоимости введем формулу в ячейку D2: = цена за единицу * количество. Константы формулы – ссылки на ячейки с соответствующими значениями.
3. Нажимаем ВВОД – программа отображает значение умножения. Те же манипуляции необходимо произвести для всех ячеек. Как в Excel задать формулу для столбца: копируем формулу из первой ячейки в другие строки. Относительные ссылки – в помощь.
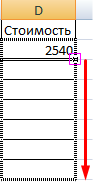
Находим в правом нижнем углу первой ячейки столбца маркер автозаполнения. Нажимаем на эту точку левой кнопкой мыши, держим ее и «тащим» вниз по столбцу.
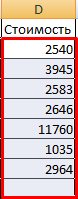
Отпускаем кнопку мыши – формула скопируется в выбранные ячейки с относительными ссылками. То есть в каждой ячейке будет своя формула со своими аргументами.
Ссылки в ячейке соотнесены со строкой.
Формула с абсолютной ссылкой ссылается на одну и ту же ячейку. То есть при автозаполнении или копировании константа остается неизменной (или постоянной).
Чтобы указать Excel на абсолютную ссылку, пользователю необходимо поставить знак доллара ($). Проще всего это сделать с помощью клавиши F4.
2. Воспользуемся функцией автозаполнения. Кнопка находится на вкладке «Главная» в группе инструментов «Редактирование».
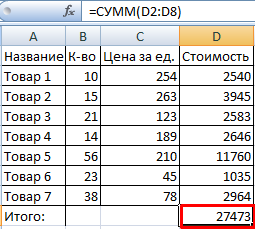
3. После нажатия на значок «Сумма» (или комбинации клавиш ALT+«=») слаживаются выделенные числа и отображается результат в пустой ячейке.
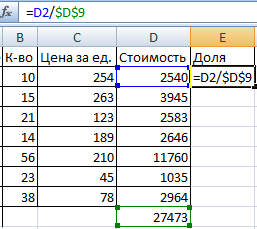
Сделаем еще один столбец, где рассчитаем долю каждого товара в общей стоимости. Для этого нужно:
2. Чтобы получить проценты в Excel, не обязательно умножать частное на 100. Выделяем ячейку с результатом и нажимаем «Процентный формат». Или нажимаем комбинацию горячих клавиш: CTRL+SHIFT+5
3. Копируем формулу на весь столбец: меняется только первое значение в формуле (относительная ссылка). Второе (абсолютная ссылка) остается прежним. Проверим правильность вычислений – найдем итог. 100%. Все правильно.
При создании формул используются следующие форматы абсолютных ссылок:
КАК СОСТАВИТЬ ТАБЛИЦУ В EXCEL С ФОРМУЛАМИ
Чтобы сэкономить время при введении однотипных формул в ячейки таблицы, применяются маркеры автозаполнения. Если нужно закрепить ссылку, делаем ее абсолютной. Для изменения значений при копировании относительной ссылки.
Простейшие формулы заполнения таблиц в Excel:
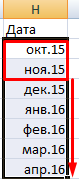
3.По такому же принципу можно заполнить, например, даты. Если промежутки между ними одинаковые – день, месяц, год. Введем в первую ячейку «окт.15», во вторую – «ноя.15». Выделим первые две ячейки и «протянем» за маркер вниз.
Чтобы проверить правильность вставленной формулы, дважды щелкните по ячейке с результатом.
Ну вот! Теперь мы умеем создавать формулы и таблицы в Excel.
Дорогой читатель! Добавьте этот сайт в закладки своего браузера и поделитесь с друзьями ссылкой на этот сайт! Мы стараемся показывать здесь всякие хитрости и секреты. Пригодится точно.
Статья на тему «Решение текстовых задач с использованием таблиц»
Решение текстовых задач с использованием таблиц.
учитель математики МБОУ «Гимназия № 94»
Московского района города Казани
Не секрет, что при решении текстовых задач, в которых вводится неизвестная переменная и составляется уравнение (или система уравнений), многие учащиеся испытывают затруднения. Часто возникают вопросы: что взять за неизвестную переменную, какое условие взять за основу уравнения при решении задачи, как правильно осмыслить те данные, которые приведены в задаче.
При решении задач удобно использовать таблицы, в которые вносятся условия. Информация, размещенная в таблице, позволяет конкретизировать иногда витиеватые условия задачи, более четко в них разобраться. И на основании заполненных ячеек таблицы составить уравнение для решения.
Рассмотрим следующие типы задач:
Задачи на движение.
Задачи на движение по воде.
Задачи на нахождение средней скорости.
Задачи на производительность труда и совместную работу.
Задачи на концентрацию, смеси и сплавы.
Задачи на движение
Основной формулой, используемой в задачах, является формула расстояния S = V * t .
Рассмотрим случай, когда решение текстовой задачи сводится к решению дробно-рационального уравнения.
В большинстве случаев за х (неизвестную переменную) берется скорость. Совет: Лучше брать за х то, о чем спрашивается в задаче.
Таблица, для заполнения условий задачи имеет вид:
Получаем формулу для составления уравнения: t 1 — t 2 = к. (1)
( От большего вычитаем меньшее получаем разницу).
Используя таблицу подставляем в уравнение (1) выражения для t 1 и t 2 ( t 1 = S 1 : V 1 ; t 2 = S 2 : V 2 ). Получаем дробно-рациональное уравнение. Уравнение обычно сводится к решению квадратного уравнения, при решении которого получаем два корня. Отбрасываем корень, который не удовлетворяет условию задачи.
Совет: при решении уравнения часто получаются большие коэффициенты. Не старайтесь сразу умножать числа, возможно их можно будет сократить.
Пусть скорость пешехода, шедшего из А равна х км/ч, тогда скорость пешехода шедшего из В равна (х-2)км/ч.
Пешеход из А прошел 15 км, а расстояние между пунктами 27 км, следовательно пешеход их В прошел 12 км.
Формула для составления уравнения имеет вид: t 2 — t 1 = 0,5.
Получаем уравнение 

Решаем его: 
Корень х=-10 не удовлетворяет условию задачи. Получаем, что скорость пешехода из А равна 6 км/ч.
Ответ : скорость пешехода из А равна 6 км/ч.
Задачи для самостоятельного решения.
Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
Два автомобиля одновременно отправляются в 240-километровый пробег. Первый едет со скоростью, на 20 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 40 минут раньше, чем велосипедист приехал в А, а встретились они через 15 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 30 км/ч, а вторую половину пути проехал со скоростью, большей скорости первого на 9 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста.
Расстояние между городами А и В равно 120 км. Из города А в город В выехал автомобиль, а через 90 минут следом за ним со скоростью 100 км/ч выехал мотоциклист. Мотоциклист догнал автомобиль в городе С и повернул обратно. Когда он проехал половину пути из С в А, автомобиль прибыл в В. Найдите расстояние от А до С.
Задачи на движение по воде.
В задачах при движении по воде используются четыре вида скорости.
Собственная скорость (лодки, катера, теплохода…).
Скорость течения реки.
Скорость по течению реки.
Скорость против течения реки.
Примечание: Скорость по озеру = скорости лодки.
Скорость плота = скорости течения реки.
За неизвестную переменную принимают скорость течения реки или скорость лодки, а именно то, что нужно найти в задаче. Берем за х (ед. из.) скорость лодки, а у – скорость течения реки.
Таблица, для заполнения условий задачи имеет вид:
Против течения реки
Количество строк зависит от условия конкретной задачи.
Моторная лодка прошла 14 км против течения реки, а затем прошла еще 17км по течению реки, затратив на это один час. Найдите скорость моторной лодки в стоячей воде, если скорость течения реки 3 км/ч.
Пусть скорость моторной лодки х км/ч.
Против течения реки
Уравнение составляется исходя из условия: t 1 + t 2 =1.



Данное уравнение равносильно системе:
Корень х=0 не удовлетворяет условию задачи. Получаем, что скорость моторной лодки равна 31 км/ч.
Ответ: скорость моторной лодки 31 км/ч.
Задачи для самостоятельного решения.
Теплоход проходит по течению реки до пункта назначения 280 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 15 часов, а в пункт отправления теплоход возвращается через 39 часов после отплытия из него.
Расстояние между пристанями А и В равно 63 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 20 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч.
От пристани А к пристани В, расстояние между которыми равно 70 км, отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним, со скоростью, на 8 км/ч большей, отправился второй. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно.
Моторная лодка прошла от одной пристани до другой, расстояние между которыми по реке равно 16 км, сделала стоянку на 40 мин и вернулась обратно через 3 
Пристани А и В расположены на реке, скорость течения которой на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
Баржа прошла по течению реки 40 км и, повернув обратно, прошла ещё 30 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5 км/ч.
Задачи на нахождение средней скорости.
Используем формулу V средняя = 
Решаем задачи по математике: практическое руководство для родителей
Рассказываем, как научить ребёнка превращать дано в итого быстро и интересно.
На протяжении всего обучения школьникам приходится решать задачи — в начальной школе по математике, а затем по алгебре, геометрии, физике и химии. И хотя условия задач в разных науках отличаются, способы решения основаны на одних и тех же логических принципах. Понимание того, как устроена простая задача по математике, поможет ребёнку разработать алгоритмы для решения задач из других областей науки. Поэтому учить ребёнка решать задачи необходимо уже с первого класса.
Нередки случаи, когда точные науки вызывают у детей сопротивление. Видя это, учителя и родители записывают таких детей в «гуманитарии», из-за чего они только укрепляются во мнении, что точные науки — это не для них. Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер:
Детям вбивают в голову, что математика — это сложно. К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.
Чтобы ребёнку было интересно учить математику, он должен понимать, как эти знания пригодятся ему, даже если он не собирается становиться программистом или инженером.
Математика ежедневно помогает нам считать деньги, без умения вычислять периметр и площадь невозможно сделать ремонт, а навык составления пропорций незаменим в кулинарии — используйте это. Превращайте ежедневные бытовые вопросы в математические задачи для ребёнка: пусть польза математики станет для него очевидна.
Конечно, найти в быту применение иррациональным числам или квадратным уравнениям не так просто. И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям».
Как правильно научить ребёнка решать задачи
Если ребёнок только начинает осваивать навык решения задач, приучите его придерживаться определённого алгоритма.
1. Внимательно читаем условия
Лучше вслух и несколько раз. После того как ребёнок прочитал задачу, задайте ему вопросы по тексту и убедитесь, что ему понятно, что вычислять нужно количество грибов, а не огурцов. Старайтесь не нервничать, если ребёнок упустил что-то из вида. Дайте ему разобраться самостоятельно. Если в условиях упоминаются неизвестные ребёнку реалии — объясните, о чём идёт речь.
Особую сложность представляют задачи с косвенным вопросом, например:
«Один динозавр съел 16 деревьев, это на 3 меньше, чем съел второй динозавр. Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.
2. Делаем описание задачи
В решении некоторых задач поможет представление данных в виде схемы, графика или рисунка. Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе.
Ребёнок должен чётко понимать значения словесных формул и знать, какие математические действия им соответствуют.
3. Выбор способа решения
Наглядно записанное условие должно подтолкнуть ребёнка к нахождению решения. Если этого не произошло, попробуйте задать наводящие вопросы, проиллюстрировать задачу при помощи окружающих предметов или разыграть сценку. Если один из способов объяснения не сработал — придумайте другой. Многократное повторение одного и того же вопроса неэффективно.
Все, даже самые сложные, математические задачи сводятся к принципу «из двух известных получаем неизвестное». Но для нахождения этой пары чисел часто требуется выполнить несколько действий, то есть разложить задачу на несколько более простых.
Ребёнок должен знать способы получения неизвестных данных из двух известных:
После того как план действий найден, подробно запишите решение. Оно должно отражать всю последовательность действий — так ребёнок сможет запомнить принцип и пользоваться им в дальнейшем.
4. Формулировка ответа
Ответ должен быть полным и точным. Это не просто формальность: обдумывая ответ, ребёнок привыкает серьёзно относиться к результатам своего труда. А главное — из описания должна быть понятна логика решения.
Одна из самых распространённых ошибок — представление в ответе не тех данных, о которых спрашивалось изначально. Если такая проблема возникает, нужно вернуться к первому пункту.
5. Закрепление результата
Не стоит думать, что выполнив задание один раз, ребёнок сразу научится решать задачи. Полученный результат нужно зафиксировать. Для этого подумайте над решённой задачей ещё немного: предложите ребёнку поискать другой способ решения или спросите, как изменится ответ при изменении того или иного параметра в условии.
Важно, чтобы у ребёнка сложился чёткий алгоритм рассуждений и действий в каждом из вариантов.
В нашей онлайн-школе, помимо уроков, ученики могут закреплять свои знания на консультациях в формате открытых часов, где учителя разбирают темы, вызвавшие затруднения, показывают необычные задачи и различные способы их решения.
Что поможет ребёнку решать задачи
В заключение расскажем о том, как сделать процесс решения задач проще и интереснее:
После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.












.png)
