Чем больше число рейнольдса тем

Рейнольдса число

Число Рейно́льдса — безразмерное соотношение, которое, как принято считать, определяет ламинарный или турбулентный режим течения жидкости или газа. Число Рейнольдса также считается критерием подобия потоков.

Число Рейнольдса определяется следующим соотношением: 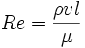, где ρ — плотность среды, v — характерная скорость, l — характерный размер, μ — динамическая вязкость среды.

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, в водохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение.

Критерий назван в честь выдающегося английского физика О. Рейнольдса (англ.)(1842—1912), автора многочисленных пионерских работ по гидродинамике.

Физический смысл

Число Рейнольдса есть отношение сил инерции, действующих в потоке, к силам вязкости. Также число Рейнольдса можно рассматривать как отношение кинетической энергии жидкости к потерям энергии на характерной длине.

Безразмерные числа в физикеПонятияРазмерность физической величины · Безразмерное число · П-теорема · Критерий подобияЧислаАббе · Архимеда · Багнольда · Био · Бонда · Бринкмана · Вебера · Вайсенберга · Гагена · Галилея · Гартмана · Грасхофа · Гуше · Дамкёлера · Деборы · Дерягина · Гретца · Дина · Каулинга · капиллярности · Кнудсена · Лапласа · Льюиса · Маха · Марангони · Нуссельта · Онезорге · Пекле · Прандтля (магнитное, турбулентное) · Рейнольдса (магнитное) · Ричардсона · Россби · Роуза · Рошко · Руарка · Рэлея · Стентона · Стокса · Струхаля · Суратмана · Тейлора · Уомерсли · Фруда · Фурье · Чандрасекара · Шмидта · Шервуда · Эйлера · Эккерта · Экмана · Элсассера · Эотвоша

Полезное

Смотреть что такое «Рейнольдса число» в других словарях:

РЕЙНОЛЬДСА ЧИСЛО — (по имени англ. учёного О. Рейнольдса (О. Reynolds)), один из подобия критериев для течений вязких жидкостей и газов, характеризующий соотношение между инерц. силами и силами вязкости: Re=rvl/m, где r плотность, m коэфф. динамич. вязкости… … Физическая энциклопедия

Рейнольдса число — (по имени О. Рейнольдса) безразмерный параметр, характеризующий собой соотношение инерционных сил и сил внутреннего трения в потоке жидкости или газа. Равен произведению плотности (е), характерных значений скорости V и линейного размера L,… … Энциклопедия техники

Рейнольдса число — безразмерная величина, являющаяся одной из основных характеристик течения вязкой жидкости и равная отношению сил инерции к силам вязкости: Re = ρvl/μ, где ρ плотность жидкости, v характерная скорость (например, скорость потока), l характерный… … Энциклопедический словарь

Рейнольдса число — Reinoldso skaičius statusas T sritis Energetika apibrėžtis Apibrėžtį žr. priede. priedas( ai) MS Word formatas atitikmenys: angl. Reynolds number vok. Reynolds Zahl, f rus. Рейнольдса число, n pranc. nombre de Reynolds, m … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas

Рейнольдса число — (по имени О. Рейнольдса) — безразмерный параметр, характеризующий собой соотношение инерционных сил и сил внутреннего трения в потоке жидкости или газа. Равен произведению плотности ρ, характерных значений скорости V и линейного размера L,… … Энциклопедия «Авиация»

Рейнольдса число — (по имени О. Рейнольдса) — безразмерный параметр, характеризующий собой соотношение инерционных сил и сил внутреннего трения в потоке жидкости или газа. Равен произведению плотности ρ, характерных значений скорости V и линейного размера L,… … Энциклопедия «Авиация»

Рейнольдса число — один из подобия критериев (См. Подобия критерии) для течений вязких жидкостей и газов, характеризующий соотношение между инерционными силами и силами вязкости: Re = ρvl/μ, где ρ плотность, μ динамический коэффициент вязкости жидкости или… … Большая советская энциклопедия

РЕЙНОЛЬДСА ЧИСЛО — один из критериев подобия для течений вязких жидкостей и газов, характеризующий соотношение между инерционными силами и силами вязкости: где r плотность, m динамич. коэффициент вязкости жидкости или газа, v характерная скорость потока, l… … Математическая энциклопедия

РЕЙНОЛЬДСА ЧИСЛО — безразмерная величина, являющаяся одной из осн. характеристик течения вязкой жидкости и равная отношению сил инерции к силам вязкости: Re = pvl/n, где р плотность жидкости, v характерная скорость (напр., скорость потока), l характерный линейный… … Естествознание. Энциклопедический словарь

Источник

Основы гидравлики

Режимы движения реальных жидкостей

Почему так происходит, и в какой момент в спокойном и ласковом потоке вдруг просыпается безумный бурлящий «демон»? Можно ли предсказать поведение потока в тех или иных условиях?
Давайте попробуем разобраться в этом вопросе с точки зрения современной науки.

Рассмотрим потоки, характеризуемые условием неразрывности – в любой момент времени расход жидкости постоянен во всех сечениях, т. е соблюдается соотношение:

Число Рейнольдса

Влияние всех этих величин на характер движения жидкости объединены в формуле, выражающей число Рейнольдса:

Число Рейнольдса (иногда его называют критерием Рейнольдса) является безразмерной величиной.

Формулу (1) применяют при определении числа Рейнольдса для потока любого сечения.
Для круглых цилиндрических труб с внутренним диаметром d :

При проведении гидравлических расчетов цилиндрических труб обычно принимают Re = 250…500, Re’_кр = 575. При этом Re_d будет равен: Red_кр = 1000…2000, Red’_кр = 2300.

Проведенные исследования показывают также, что критическое значение числа Рейнольдса увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это можно объяснить тем, что при ускорении движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах увеличивается.

По критическому значению числа Рейнольдса легко можно определить также критическую скорость, т. е. скорость, ниже которой будет иметь место ламинарное движение жидкости:

Ламинарному и турбулентному режимам движения жидкости соответствует и различное распределение скоростей частиц по живому сечению потока.

Пример решения задачи с использованием числа Рейнольдса

Определим число Рейнольдса для данного режима движения жидкости (нефти) :

Другие задачи на использование числа Рейнольдса для определения режимов движения жидкостей представлены здесь.

Источник

Число Рейнольдса имеет широкое применение: от потока жидкости в трубе до прохождения воздуха над крылом самолета. Он используется для прогнозирования перехода от ламинарного к турбулентному потоку и используется при масштабировании аналогичных, но разных по размеру ситуаций потока, например, между моделью самолета в аэродинамической трубе и полноразмерной версией. Прогнозы начала турбулентности и возможность расчета масштабных эффектов могут использоваться для помощи в прогнозировании поведения флюидов в более крупном масштабе, например, в локальном или глобальном движении воздуха или воды и, таким образом, связанных с ними метеорологических и климатологических эффектов.

Эта концепция была введена Джорджем Стоуксом в 1851 году, но число Рейнольдса было названо Арнольдом Зоммерфельдом в 1908 году в честь Осборна Рейнольдса (1842–1912), который популяризировал его использование в 1883 году.

СОДЕРЖАНИЕ

Определение

Эта способность прогнозировать начало турбулентного потока является важным инструментом проектирования для такого оборудования, как системы трубопроводов или крылья самолета, но число Рейнольдса также используется при масштабировании задач гидродинамики и используется для определения динамического сходства между двумя различными случаями поток жидкости, например, между моделью самолета и его полноразмерной версией. Такое масштабирование не является линейным, и применение чисел Рейнольдса к обеим ситуациям позволяет разработать коэффициенты масштабирования.

Число Рейнольдса определяется как

р е знак равно ты L ν знак равно ρ ты L μ <\ displaystyle \ mathrm = <\ frac

<\ nu>> = <\ frac <\ rho uL><\ mu>>>

На практике сопоставление числа Рейнольдса само по себе недостаточно, чтобы гарантировать сходство. Поток жидкости обычно хаотичен, и очень небольшие изменения формы и шероховатости ограничивающих поверхностей могут привести к очень разным потокам. Тем не менее, числа Рейнольдса являются очень важным ориентиром и широко используются.

История

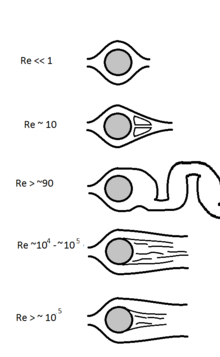
Большая труба была стеклянной, чтобы можно было наблюдать за поведением слоя окрашенного потока, а на конце этой трубы был клапан регулирования потока, используемый для изменения скорости воды внутри трубы. Когда скорость была низкой, окрашенный слой оставался отчетливым по всей длине большой трубки. Когда скорость увеличивалась, слой разрушался в заданной точке и распространялся по поперечному сечению жидкости. Точка, в которой это произошло, была точкой перехода от ламинарного течения к турбулентному.

Поток в трубе

Для потока в трубе или трубе число Рейнольдса обычно определяется как

Для круглой трубы гидравлический диаметр точно равен внутреннему диаметру трубы:

Для расчета потока в воздуховодах некруглого сечения диаметр воздуховода круглого сечения может быть заменен гидравлическим диаметром с достаточной точностью, если аспектное отношение AR поперечного сечения воздуховода остается в диапазоне 1 / 4

Ламинарно-турбулентный переход

Эти переходные числа Рейнольдса также называются критическими числами Рейнольдса и были изучены Осборном Рейнольдсом около 1895 года. Критическое число Рейнольдса различно для каждой геометрии.

Поток в широком воздуховоде

Для жидкости, движущейся между двумя плоскопараллельными поверхностями, ширина которых намного больше, чем расстояние между пластинами, характерный размер равен расстоянию между пластинами. Это согласуется с вышеупомянутыми случаями кольцевого и прямоугольного воздуховодов с ограниченным соотношением сторон.

Течение в открытом канале

Обтекание профилей

Объект в жидкости

В вязких жидкостях

Ламинарный поток полимерных растворов используется такими животными, как рыбы и дельфины, которые выделяют вязкие растворы из кожи, чтобы помочь течению по телу во время плавания. Его использовали в гонках на яхтах владельцы, которые хотят получить преимущество в скорости за счет перекачивания раствора полимера, такого как низкомолекулярный полиоксиэтилен в воде, по смоченной поверхности корпуса.

Сфера в жидкости

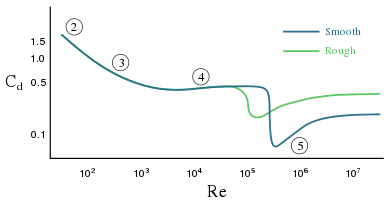
При более высоких числах Рейнольдса сопротивление сфере зависит от шероховатости поверхности. Так, например, добавление ямок на поверхности мяча для гольфа приводит к переходу пограничного слоя на входной стороне мяча от ламинарного к турбулентному. Турбулентный пограничный слой может оставаться прикрепленным к поверхности шара намного дольше, чем ламинарная граница, и поэтому создает более узкий след низкого давления и, следовательно, меньшее сопротивление давлению. Уменьшение сопротивления давления заставляет мяч двигаться дальше.

Прямоугольный объект в жидкости

Уравнение для прямоугольного объекта идентично уравнению для сферы, при этом объект аппроксимируется как эллипсоид, а ось длины выбирается в качестве характерного масштаба длины. Такие соображения важны в естественных ручьях, например, где мало идеально сферических зерен. Для зерен, в которых измерение каждой оси нецелесообразно, диаметр сита используется вместо этого в качестве характерной шкалы длины частицы. Оба приближения изменяют значения критического числа Рейнольдса.

Скорость падения

Число Рейнольдса частицы важно для определения скорости падения частицы. Когда число Рейнольдса частицы указывает на ламинарный поток, закон Стокса можно использовать для расчета скорости его падения. Когда число Рейнольдса частицы указывает на турбулентный поток, необходимо построить закон турбулентного сопротивления для моделирования соответствующей скорости осаждения.

Упакованная кровать

Ламинарные условия применяются до Re = 10, полностью турбулентные от Re = 2000.

Сосуд для перемешивания

Трение трубы

Подобие потоков

Номера моделей и номера дизайна должны быть в одинаковой пропорции, следовательно,

Наименьшие масштабы турбулентного движения

В турбулентном потоке существует диапазон масштабов изменяющегося во времени движения жидкости. Размер наибольших масштабов движения жидкости (иногда называемых водоворотами) определяется общей геометрией потока. Например, в промышленной дымовой трубе самые большие масштабы движения жидкости равны диаметру самой трубы. Размер самых маленьких шкал задается числом Рейнольдса. По мере увеличения числа Рейнольдса становятся видны все меньшие и меньшие масштабы потока. В дымовой трубе дым может иметь множество очень небольших возмущений скорости или завихрений в дополнение к большим объемным водоворотам. В этом смысле число Рейнольдса является индикатором диапазона масштабов в потоке. Чем выше число Рейнольдса, тем больше диапазон шкал. Самые большие водовороты всегда будут одного размера; самые маленькие водовороты определяются числом Рейнольдса.

В физиологии

Используя определение числа Рейнольдса, мы можем видеть, что большой диаметр с быстрым потоком, где плотность крови высока, имеет тенденцию к турбулентности. Быстрые изменения диаметра сосуда могут привести к турбулентному потоку, например, когда более узкий сосуд расширяется до большего. Кроме того, выпуклость атеромы может быть причиной турбулентного потока, при котором слышимая турбулентность может быть обнаружена с помощью стетоскопа.

Комплексные системы

Вывод

Число Рейнольдса можно получить, если использовать безразмерную форму несжимаемых уравнений Навье – Стокса для ньютоновской жидкости, выраженную через производную Лагранжа :

Если мы теперь установим

мы можем переписать уравнение Навье – Стокса без размерностей:

Наконец, отбросим простые числа для удобства чтения:

Связь с другими безразмерными параметрами

Источник

Число Рейнольдса: для чего оно нужно, как рассчитывается, упражнения

Содержание:

Число Рейнольдса применяется к любому типу потока жидкости, например к потоку в круглых или некруглых каналах, в открытых каналах и потоке вокруг погруженных тел.

Значение числа Рейнольдса зависит от плотности, вязкости, скорости жидкости и размеров пути тока. Поведение жидкости в зависимости от количества энергии, которая рассеивается из-за трения, будет зависеть от того, является ли поток ламинарным, турбулентным или промежуточным. По этой причине необходимо найти способ определения типа потока.

В 1883 году Осборн Рейнольдс обнаружил, что, если значение этого безразмерного числа известно, можно предсказать тип потока, который характеризует любую ситуацию с проводимостью жидкости.

Для чего нужно число Рейнольдса?

Число Рейнольдса используется для определения поведения жидкости, то есть для определения того, является ли течение жидкости ламинарным или турбулентным. Течение является ламинарным, когда силы вязкости, которые противодействуют движению жидкости, являются доминирующими, и жидкость движется с достаточно малой скоростью и по прямолинейному пути.

Жидкость с ламинарным потоком ведет себя так, как будто это бесконечные слои, которые упорядоченно скользят друг по другу без перемешивания. В круглых воздуховодах ламинарный поток имеет параболический профиль скорости с максимальными значениями в центре воздуховода и минимальными значениями в слоях вблизи поверхности воздуховода. Значение числа Рейнольдса в ламинарном потоке равно р_{а также} 4000.

Переход между ламинарным потоком и турбулентным потоком происходит для значений числа Рейнольдса между 2000 Y 4000.

Как рассчитывается?

Уравнение, используемое для расчета числа Рейнольдса в воздуховоде круглого сечения:

ρ = Плотность жидкости (кг / м 3 )

V = Скорость потока (м 3 / с)

D = Характерный линейный размер пути прохождения жидкости, который в случае круглого воздуховода представляет собой диаметр.

η = динамическая вязкость жидкости (Па · с)

Связь между вязкостью и плотностью определяется как кинематическая вязкость. v = η/ρ, и его единица м 2 / с.

Уравнение числа Рейнольдса как функции кинематической вязкости:

В трубопроводах и каналах с некруглым поперечным сечением характерный размер известен как гидравлический диаметр. D_ЧАС y представляет собой обобщенный размер пути прохождения жидкости.

Обобщенное уравнение для расчета числа Рейнольдса в трубопроводах с некруглым поперечным сечением:

V´ = Средняя скорость потока =Идет

Мокрый периметр п_M представляет собой сумму длин стенок трубопровода или канала, контактирующих с жидкостью.

Вы также можете рассчитать число Рейнольдса жидкости, окружающей объект. Например, сфера, погруженная в жидкость, движущуюся со скоростью V. Сфера испытывает силу сопротивления F_р определяется уравнением Стокса.

Число Рейнольдса шара со скоростью V погруженные в жидкость:

р_{а также} 1 при турбулентном потоке.

Решенные упражнения

Ниже приведены три упражнения по применению числа Рейнольдса: Круглый канал, Прямоугольный канал и Сфера, погруженная в жидкость.

Число Рейнольдса в воздуховоде круглого сечения

Рассчитайте число Рейнольдса пропиленгликоля a 20°C в воздуховоде круглого сечения диаметром 0,5 см. Величина скорости потока равна 0,15 м 3 / с. Какой тип потока?

Плотность жидкости составляет ρ = 1,036 г / см 3 = 1036 кг / м 3

Вязкость жидкости составляет η =0,042 Па · с = 0,042 кг / м.с

Скорость потока V = 0,15 м 3 / с

Уравнение числа Рейнольдса используется для круглого воздуховода.

Течение ламинарное, потому что значение числа Рейнольдса мало по отношению к соотношению р_{а также} 3

Сначала определяется средняя скорость потока.

Гидравлический диаметр D_ЧАС = 4А / П_M

Число Рейнольдса получается из уравнения р_{а также} = ρV´ D_ЧАС/η

Течение является турбулентным, поскольку число Рейнольдса очень велико (р_{а также}>2000)

Число Рейнольдса для сферы, погруженной в жидкость

Сферическая частица латексного полистирола радиусом р= 2000 нм брошен вертикально в воду с начальной скоростью величинойV₀= 10 м / с. Определите число Рейнольдса частицы, погруженной в воду.

Плотность частицρ=1,04 г / см 3 = 1040 кг / м 3

Число Рейнольдса получается из уравнения р_{а также} = ρV R/η

р_{а также} = (1000 кг / м 3 Икс10 м / с Икс 0,000002 м) / 0,001 кг / (м с)

Число Рейнольдса 20. Течение турбулентное.

Приложения

Число Рейнольдса играет важную роль в механике жидкости и теплопередаче, потому что это один из основных параметров, характеризующих жидкость. Некоторые из его приложений упомянуты ниже.

1-Он используется для моделирования движения организмов, которые перемещаются по жидким поверхностям, таких как: бактерии, взвешенные в воде, которые плавают в жидкости и вызывают беспорядочное движение.

2-Он имеет практическое применение в потоках труб и в каналах циркуляции жидкости, в ограниченных потоках, особенно в пористых средах.

3-В суспензиях твердых частиц, погруженных в жидкость и в эмульсиях.

4-Число Рейнольдса применяется при испытаниях в аэродинамической трубе для изучения аэродинамических свойств различных поверхностей, особенно в случае полетов самолетов.

5-Он используется для моделирования движения насекомых в воздухе.

6-Конструкция химических реакторов требует использования числа Рейнольдса для выбора модели потока с учетом потерь напора, потребления энергии и площади передачи тепла.

7-В прогнозировании теплопередачи электронных компонентов (1).

8-В процессе полива садов и огородов необходимо знать поток воды, выходящей из труб. Чтобы получить эту информацию, определяется гидравлическая потеря напора, которая связана с трением, которое существует между водой и стенками трубы. Потеря напора рассчитывается после получения числа Рейнольдса.

Приложения в биологии

В биологии изучение движения живых организмов в воде или в жидкостях со свойствами, подобными воде, требует получения числа Рейнольдса, которое будет зависеть от размера организмов и скорости, с которой они перемещаются. сместить.

Бактерии и одноклеточные организмы имеют очень низкое число Рейнольдса (р_{а также}1), следовательно, течение имеет ламинарный профиль скорости с преобладанием вязких сил.

Организмы, близкие по размеру к муравьям (до 1 см), имеют число Рейнольдса порядка 1, что соответствует переходному режиму, в котором силы инерции, действующие на организм, столь же важны, как и силы вязкости жидкости.

У более крупных организмов, таких как люди, число Рейнольдса очень велико (р_{а также}1).

Источник

Жизнь при малом Re

Число Рейнольдса (Re) — это безразмерный параметр среды, который показывает, насколько среда может быть турбулентной на разных масштабах. Это число показывает отношение «сил инерции» некоторого тела к силе трения, возникающей из-за вязкости жидкости, в которую это тело погружено. В этой задаче предлагается вывести формулу для числа Рейнольдса и оценить его значение для плавающего в воде человека, для маленькой бактерии и для морского гребешка, попавшего в очень вязкую жидкость.

Движение жидкостей и газов описывается уравнением Навье — Стокса:

\[ \rho\frac<\partial \boldsymbol> <\partial t>+ \rho \left(\boldsymbol\cdot\nabla\right)\boldsymbol = \eta\nabla^2 \boldsymbol— \nabla p. \]

Здесь \(\rho\) — плотность жидкости, \(\boldsymbol\) — ее скорость (это вектор), \(\eta\) — ее вязкость и \(p\) — давление. Символом \(\nabla\) обозначается векторный оператор Гамильтона (хотя обычно его так и называют — оператор набла), а \(\nabla^2\) — оператор Лапласа. Точка в выражении \(\boldsymbol\cdot\nabla\) — это скалярное умножение. Но если вы не знаете производных, то не пугайтесь, дальше их практически не будет. Сейчас мы упростим вид уравнения и сведем все к более привычным терминам. Надо понимать, что на самом деле уравнение Навье — Стокса — это просто запись второго закона Ньютона \(ma = F\) для тела в жидкости: ускорение тела обусловлено действующими на него силами.

Теперь становится понятным, что правая часть уравнения — это просто сила \(\boldsymbol\), действующая на единицу объема воды, а левая — это просто ускорение (сила инерции). Давайте еще сильнее упростим это уравнение, избавившись от производных и рассматривая движение только в одном измерении. Рассмотрим ситуацию на небольшом участке времени \(\Delta t\) и небольшом участке пространства \(\Delta x\). Тогда уравнение Навье — Стокса будет выглядеть совсем просто:

Первый член в правой части — это сила трения вязкой жидкости (\(\Delta x^2\) появилось в знаменателе из-за упрощения второй производной), второй член — это сила, возникающая из-за разности давлений (по сути, «сила Архимеда»).

Задача

Итак, число Рейнольдса — это безразмерная величина, равная отношению сил инерции (стоящих в левой части уравнения Навье-Стокса) к силе вязкого трения. Найдите выражение для числа Рейнольдса для объекта размером \(D\), движущегося в жидкости плотностью \(\rho\) и вязкостью \(\eta\) со скоростью \(v\).

В задаче Масштабы турбулентности мы говорили о том, что человек в быту в основном соприкасается с миром больших чисел Рейнольдса. Но насколько этот мир отличается от мира, где числа Рейнольдса малы? Оцените численное значение для человека, плывущего в воде, и для бактерии размером в несколько микрон, плывущей со скоростью 30 мкм в секунду (вязкость воды можно принять равной 10 −2 в единицах СГС).

Насколько важна инерция для бактерии? Как далеко она проплывет, если перестанет двигаться? Рассмотрим морского гребешка (рис. 1), пытающегося плыть в очень вязкой жидкости (с малым числом Рейнольдса), периодически открывая и закрывая створки. Как быстро он будет передвигаться?

Рис. 1. Последовательность движений морского гребешка, который пытается плыть в вязкой жидкости

Подсказка 1

Для оценки числа Рейнольдса характерные масштабы изменений \(\Delta x\) нужно брать равными размеру объектов, \(D\).

Подсказка 2

Подумайте, какие из членов в уравнении Навье — Стокса важны, а какие не важны, если число Рейнольдса мало.

Решение

Разделим инерциальный член уравнения Навье — Стокса на силу трения:

Выражение \(\Delta x/\Delta t\) — это, по сути, скорость \(v\) нашего объекта. А длину \(\Delta x\), на масштабах которой мы рассматриваем уравнение Навье — Стокса, можно взять равной размеру объекта в воде — это характерный масштаб, на котором меняются наши величины. Таким образом, получим:

Для плывущего человека примем \(D=1\) м, \(v = 1\) м/с. Подставив плотность и вязкость воды, получим \(Re \sim 10^6 \gg 1\). С другой стороны, для бактерии получится \(Re \sim 10^<-5>\text<->10^ <-4>\ll 1\).

О чем же говорит этот результат: для человека число Рейнольдса много больше единицы, а для бактерии — много меньше единицы? Представим, что мы «толкаем» бактерию в воде с некоторой скоростью (скажем, 100 микрон в секунду) и в некоторый момент отпускаем. Бактерия начнет тормозить из-за силы вязкого трения. Ускорение (точнее, скорость торможения) бактерии будет равно

(где \(\Delta x\) можно принять равным \(D\)), а время торможения получится равным

За такое время тормозящая бактерия проплывет всего лишь \(v\Delta t = 0<,>1\) нанометр, то есть 1/10000 размера своего тела. Иными словами, бактерия практически мгновенно остановится из-за трения, не проплыв по инерции практически ничего.

Послесловие

В этом выводе и содержится главное отличие между «мирами» больших и малых чисел Рейнольдса: при малых значениях числа Рейнольдса инерция и время не имеют значения. В таком мире тела не могут передвигаться по инерции: чтобы не останавливаться, они должны продолжать двигаться, «отталкиваясь» от среды. В мире же больших чисел Рейнольдса движение, по сути, реактивное: вы толкаете воду в обратном направлении, и движетесь вперед по инерции за счет сохранения импульса.

Еще одним следствием того, что время не имеет значения, является то, что все движения обратимы. Иными словами, если в вязкой среде вы совершаете некоторое движение своим телом, передвигаясь в некотором направлении, а затем повторите это же движение в точности, но наоборот, то вернетесь в ту же точку, откуда начинали. Наглядную демонстрацию этого можно увидеть в ролике Дестина Сандлина (YouTube-канал SmarterEveryDay):