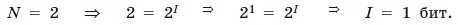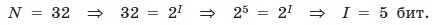Чем больше количество знаков содержит алфавит знаковой системы тем большее количество информации
Тема 2.1 Представление и обработка информации
С позиции человека информация— это содержание разных сообщений, это самые разнообразные сведения, которые человек получает от окружающего мира через свои органы чувств.
Теория информации. результат развития теории связи (К.Шеннон) Информация-содержание, заложенное в знаковые ( сигнальные последовательности).
Кибернетика. Исследует информационные процессы в системах управления (Н. Винер). Информация- содержание сигналов, передаваемых по каналам связи в системах управления.
Нейрофизиология. Изучает информационные процессы в механизмах нервной деятельности животного и человека. Информация- содержание сигналов электрохимической природы, передающихся по нервным волокнам организма.
Генетика. Изучает механизмы наследственности, пользуется понятием «наследственная информация». Информация- содержание генетического кода- структуру молекул ДНК, входящих в состав клетки живого организма.
Философия. Атрибутивная концепция: Информация- всеобщее свойство (атрибут) материи.
Функциональная концепция: Информация и информационные процессы присущи только живой природе, являются ее функцией.
Антропоцентрическая концепция: Информация и информационные процессы присущи только человеку.
Понятие информации относится к числу фундаментальных, т.е. является основополагающим для науки и не объясняется через другие понятия.
В этом смысле информация встает в один ряд с такими фундаментальными научными понятиями, как вещество, энергия, пространство, время.
Содержательный (вероятностный) подход к измерению информации
Существует два подхода к измерению информации: содержательный (вероятностный) и объемный (алфавитный).
Процесс познания окружающего мира приводит к накоплению информации в форме знаний (фактов, научных теорий и т.д.). Получение новой информации приводит к расширению знания или к уменьшению неопределенности знаний. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию.
Пусть у нас имеется монета, которую мы бросаем. С равной вероятностью произойдет одно из двух возможных событий – монета окажется в одном из двух положений: «орел» или «решка». Можно говорить, что события равновероятны.
Перед броском существует неопределенность наших знаний (возможны два события), и, как упадет монета, предсказать невозможно. После броска наступает полная определенность, так как мы видим, что монета в данный момент находится в определенном положении (например, «орел»). Это сообщение приводит к уменьшению неопределенности наших знаний в два раза, так как до броска мы имели два вероятных события, а после броска – только одно, то есть в два раза меньше.
Чем больше неопределенна первоначальная ситуация (возможно большее количество информационных сообщений – например, бросаем не монету, а шестигранный кубик), тем больше мы получим новой информации при получении информационного сообщения (в большее количество раз уменьшится неопределенность знания).
Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений.
Существует формула – главная формула информатики, которая связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение:
N = 2I
За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределенность знания в два раза. Такая единица названа бит.
Если вернуться к опыту с бросанием монеты, то здесь неопределенность как раз уменьшается в два раза и, следовательно, полученное количество информации равно 1 биту.
2 = 21
Бит – наименьшая единица измерения информации.
С помощью набора битов можно представить любой знак и любое число. Знаки представляются восьмиразрядными комбинациями битов – байтами.
1байт = 8 битов
Байт – это 8 битов, рассматриваемые как единое целое, основная единица компьютерных данных.
Для измерения информации используются более крупные единицы: килобайты, мегабайты, гигабайты, терабайты и т.д.
1 Кбайт = 210 байт = 1 024 байт
1 Мбайт = 220 байт = 210 Кбайт = 1 024 Кбайт = 1 048 576 байт
1 Гбайт = 230 байт = 1 024 Мбайт
1 Тбайт = 240 байт = 1 024 Гбайт
В рулетке общее количество лунок равно 32. Какое количество информации мы получим при остановке шарика в одной из лунок?
Сообщение о том, что Петя живет во втором подъезде, несет 3 бита информации. Сколько подъездов в доме?
В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил Пете, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации передал библиотекарь Пете?
При угадывании целого числа в диапазоне от 1 до N было получено 9 бит информации. Чему равно N?
Заполните пропуски числами:
5 Кбайт = __5120__байт = _40960____ бит
_1,5_Кбайт = 1536 байт = _____ бит
__Кбайт = ____ байт = 512 бит
Объемный (алфавитный) подход к измерению информации
Информация является предметом нашей деятельности: мы ее храним, передаем, принимаем, обрабатываем. Нам часто необходимо знать, достаточно ли места на носителе, чтобы разместить нужную нам информацию, сколько времени потребуется, чтобы передать информацию по каналу связи и т.п. Величина, которая нас в этих ситуациях интересует, называется объемом информации. В таком случае говорят об объемном подходе к измерению информации.
Для обмена информацией с другими людьми человек использует естественные языки (русский, английский, китайский и др.).
Наряду с естественными языками были разработаны формальные языки (системы счисления, язык алгебры, языки программирования и др.). Основное отличие формальных языков от естественных состоит в наличии строгих правил грамматики и синтаксиса. Например, системы счисления можно рассматривать как формальные языки, имеющие алфавит (цифры) и позволяющие не только именовать и записывать объекты (числа), но и выполнять над ними арифметические операции по строго определенным правилам. Некоторые языки используют в качестве знаков не буквы и цифры, а другие символы, например химические формулы, ноты, изображения элементов электрических или логических схем, дорожные знаки, точки и тире (код азбуки Морзе и др.).
Представление информации может осуществляться с помощью языков, которые являются знаковыми системами.
Каждая знаковая система строится на основе определенного алфавита и правил выполнения операций над знаками.
При хранении и передаче информации с помощью технических устройств информация рассматривается как последовательность символов – знаков (букв, цифр, кодов цветов точек изображения и т.д.)
Набор символов знаковой системы (алфавит) можно рассматривать как различные возможные состояния (события). Тогда, если считать, что появление символов в сообщении равновероятно, по формуле
N = 2I
где N – это количество знаков в алфавите знаковой системы, можно рассчитать
I – количество информации, которое несет каждый символ.
Информационная емкость знаков зависит от их количества в алфавите. Так, информационная емкость буквы в русском алфавите, если не использовать букву «ё», составляет:
В латинском алфавите 26 букв. Информационная емкость буквы латинского алфавита также 5 битов. На основании алфавитного подхода можно подсчитать количество информации в сообщении Ic, для этого необходимо умножить количество информации, которое несет один символ I, на количество символов K в сообщении:
Ic = I х K
Например: в слове «информатика» 11 знаков (К=11), каждый знак в русском алфавите несет информацию 5 битов (I=5), тогда количество информации в слове «информатика» Iс=5х11=55 (битов).
Интересно, что сама единица измерения количества информации бит (bit) получила свое название от английского словосочетания BInary digiТ, т.е. двоичная цифра.
Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак.
Мощность алфавита равна 256. Сколько Кбайт памяти потребуется для сохранения 160 страниц текста, содержащего в среднем 192 символа на каждой странице?
Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого записано это сообщение?
Сколько символов составляет сообщение, записанное с помощью 16-ти символьного алфавита, если объем его составил 1/16 часть Кбайта?
Двоичное кодирование текстовой информации
Алгоритм определения количества текстовой информации:
1. Определить кол-во символов.
2. Определить сколько бит используется для кодировки 1 символа.
3. Количество информации = число символов * число разрядов в двоичном коде.
Подсчитайте количество информации в данном тексте (бит, байт)
Двоичное кодирование графической информации
Изображение представляется в виде совокупности точек (пикселов). Точки, принадлежащие изображению, и точки, принадлежащие фону, кодируются разными знаками. Черно-белое изображение можно закодировать последовательностью:
Алгоритм определения количества графической информации:
1. Определить кол-во пиксель в изображении;
2. Определить глубину цвета.
Цветные изображения могут иметь различную глубину цвета:
2 цвета 1 пиксел – 1 бит
256 цветов 1 пиксел – 1 байт=8 бит
65536 цветов 1 пиксел – 2 байт=16 бит
3. Количество информации = количеству точек (пиксел), составляющих кадр изображения * глубина цвета.
Выполните кодирование черно-белого графического изображения. Определить количество информации (бит,байт).
Определить объем графического растрового изображения размером 50 на 50 и глубина цвета 256 цветов.
Двоичное кодирование звуковой информации.
Алгоритм определения кол-ва звуковой информации:
1. Глубина кодирования – количество различных уровней сигнала:
256 уровней – 1 байт = 8 бит
65536 уровней – 2 байта = 16 бит
2. Частота дискретизации определяется в Гц.
4. время в секундах
5. Количество звуковой информации = глубиной кодирования (бит)* частотой дискретизации (Гц)* режим звучания * время (секунды)
Определите информационный объём стереоаудиофайла длительностью звучания 5 секунд при частоте 48 КГц и глубиной кодирования 65536 уровней.
Урок 6
Алфавитный подход к измерению количества информации
§ 1.3. Количество информации
Содержание урока
1.3.3. Алфавитный подход к определению количества информации
1.3.3. Алфавитный подход к определению количества информации
При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Рис. 1.13. Передача информации
Формула (1.1) связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение. В рассматриваемой ситуации N — это количество знаков в алфавите знаковой системы, а / — количество информации, которое несет каждый знак:
С помощью этой формулы можно, например, определить количество информации, которое несет один знак в двоичной знаковой системе:
Таким образом, в двоичной знаковой системе знак несет 1 бит информации. Интересно, что сама единица измерения количества информации «бит» (bit) получила свое название от английского словосочетания «Binary digiT» — «двоичная цифра».

Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак. В качестве примера определим количество информации, которое несет буква русского алфавита. В русский алфавит входят 33 буквы, однако на практике часто для передачи сообщений используются только 32 буквы (исключается буква «ё»).
С помощью формулы (1.1) определим количество информации, которое несет одна буква русского алфавита:
Таким образом, буква русского алфавита несет 5 битов информации.
Количество информации, которое несет знак, зависит от вероятности его получения. Если получатель заранее точно знает, какой знак придет, то полученное количество информации будет равно 0. Наоборот, чем менее вероятно получение знака, тем больше его информационная емкость.
В русской письменной речи частота использования букв в тексте различна. Так, в среднем на 1000 знаков осмысленного текста приходится 200 букв «а» и в 100 раз меньшее количество буквы «ф» (всего 2). Таким образом, с точки зрения теории информации, информационная емкость знаков русского алфавита различна (у буквы «а» она наименьшая, а у буквы «ф» — наибольшая).
Количество информации в сообщении. Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Если знаки несут одинаковое количество информации, то количество информации IС в сообщении можно подсчитать, умножив количество информации I, которое несет один знак, на длину кода (количество знаков в сообщении) К:
Так, каждая цифра двоичного компьютерного кода несет 1 бит информации. Следовательно, две цифры несут 2 бита информации, три цифры — 3 бита и т. д. Количество информации в битах равно количеству цифр двоичного компьютерного кода (табл. 1.3).
Таблица 1.3. Количество информации,
которое несет двоичный компьютерный код
Задания для самостоятельного выполнения
1.8. Задание с выборочным ответом. Какое количество информации содержит один разряд двоичного числа?
1) 1 байт
2) 3 бита
3) 4 бита
4) 1 бит
1.9. Задание с кратким ответом. Какое количество информации несет двоичный код 10101010?
1.10. Задание с кратким ответом. Какова информационная емкость знака генетического кода?
Cкачать материалы урока
Презентация по информатике на тему: «Кодирование информации с помощью знаковых систем. Количество информации.» (8 класс)
Описание презентации по отдельным слайдам:
ТЕМА УРОКА: Кодирование информации с помощью знаковых систем. Количество информации. МБОУ СОШ № 279 имени Н.А.Лунина г. Гаджиево
Знаковые системы 1) Естественные языки (русский, английский. Немецкий и др.) 2) Формальные языки (системы счисления, языки программирования и др.) 3) Генетический алфавит
Кодирование информации Код – это набор условных обозначений (или сигналов) для записи (или передачи) некоторых заранее определенных понятий. Длина кода – количество знаков в коде. Перекодирование – операция преобразования знаков или группы знаков одной знаковой системы в знаки или группы знаков другой знаковой системы.
Количество информации Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационного сообщения. N = 2i, где N – количество возможных информационных сообщений, i – количество информации.
Количество информации За единицу количества информации принимается количество информации, содержащееся в информационном сообщении, уменьшающем неопределенность знания в два раза. Такая единица названа Бит.
Единицы измерения количества информации Бит – наименьшая единица измерения информации, а следующая по величине единица измерения – байт, причем: 1 байт = 8 битов = 23 битов. 1 килобайт = 210 байтов = 1024 битов 1 мегабайт = 210 Кбайт = 1024 Кбайт 1 гигабайт = 210 Мбайт = 1024 Мбайт Дискета – 1,44 Мбайт, CD-ROM – 700 Мбайт, DVD-ROM – 4,7 Гбайт
Информационная емкость знака Информационная емкость знака двоичной знаковой системы составляет 1 бит. Чем больше количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак. Пример 2: Количество информации, которое несет одна буква русского алфавита: N=32 => 32=2i => 25 = 2i => i = 5 битов.
Количество информации в сообщении Если знаки несут одинаковое количество информации, то количество информации Ic в сообщении можно подсчитать, умножив количество информации I, которое несет один знак, на длину кода (количество знаков в сообщении) K: Ic = I * K.
СПАСИБО ЗА ВНИМАНИЕ!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Методическая работа в онлайн-образовании
Курс профессиональной переподготовки
Математика и информатика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1307580
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения
Время чтения: 1 минута
Учителя Кубани смогут получить миллион рублей на взнос по ипотеке
Время чтения: 1 минута
В школах Тюмени запустят раздельный сбор отходов
Время чтения: 1 минута
Петербургский Политех создал отдельное меню для вегетарианцев в своих столовых
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Чем определяется количество информации в сообщении
Процесс познания окружающего мира приводит к накоплению информации в форме знаний (фактов, научных теорий и т. д.). Получение новой информации приводит к расширению знаний или, как иногда говорят, к уменьшению неопределенности знания. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию.
Например, после сдачи зачета или выполнения контрольной работы вы мучаетесь неопределенностью, вы не знаете, какую оценку получили. Наконец, учитель объявляет результаты, и вы получаете одно из двух информационных сообщений: «зачет» или «незачет», а после контрольной работы одно из четырех информационных сообщений: «2», «3», «4» или «5».
Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности вашего знания в два раза, так как получено одно из двух возможных информационных сообщений. Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности вашего знания в четыре раза, так как получено одно из четырех возможных информационных сообщений.
Ясно, что чем более неопределенна первоначальная ситуация (чем большее количество информационных сообщений возможно), тем больше мы получим новой информации при получении информационного сообщения (тем в большее количество раз уменьшится неопределенность знания).
Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений.
Рассмотренный выше подход к информации как мере уменьшения неопределенности знания позволяет количественно измерять информацию. Существует формула, которая связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение:
Бит. Для количественного выражения любой величины необходимо сначала определить единицу измерения. Так, для измерения длины в качестве единицы выбран метр, для измерения массы – килограмм и т. д. Аналогично, для определения количества информации необходимо ввести единицу измерения.
За единицу количества информации принимается такое количество информации, которое содержится в информационном сообщении, уменьшающем неопределенность знания в два раза. Такая единица названа битом.
Если вернуться к рассмотренному выше получению информационного сообщения о результатах зачета, то здесь неопределенность как раз уменьшается в два раза и, следовательно, количество информации, которое несет сообщение, равно 1 биту.
Производные единицы измерения количества информации. Минимальной единицей измерения количества информации является бит, а следующей по величине единицей – байт, причем:
1 байт = 8 битов = 2 3 битов.
В компьютере информация кодируется с помощью двоичной знаковой системы, и поэтому в кратных единицах измерения количества информации используется коэффициент 2 n
Так, кратные байту единицы измерения количества информации вводятся следующим образом:
1 килобайт (Кбайт) = 2 10 байт = 1024 байт;
1 мегабайт (Мбайт) = 2 10 Кбайт = 1024 Кбайт;
1 гигабайт (Гбайт) = 2 10 Мбайт = 1024 Мбайт.
- 1. Приведите примеры информационных сообщений, которые приводят к уменьшению неопределенности знания.
2. Приведите примеры информационных сообщений, которые несут 1 бит информации.
Определение количества информационных сообщений.По формуле (1.1) можно легко определить количество возможных информационных сообщений, если известно количество информации. Например, на экзамене вы берете экзаменационный билет, и учитель сообщает, что зрительное информационное сообщение о его номере несет 5 битов информации. Если вы хотите определить количество экзаменационных билетов, то достаточно определить количество возможных информационных сообщений об их номерах по формуле (1.1):
Таким образом, количество экзаменационных билетов равно 32.
Определение количества информации. Наоборот, если известно возможное количество информационных сообщений N, то для определения количества информации, которое несет сообщение, необходимо решить уравнение относительно I.
Представьте себе, что вы управляете движением робота и можете задавать направление его движения с помощью информационных сообщений: «север», «северо-восток», «восток», «юго-восток», «юг», «юго-запад», «запад» и «северо-запад» (рис. 1.11). Какое количество информации будет получать робот после каждого сообщения?
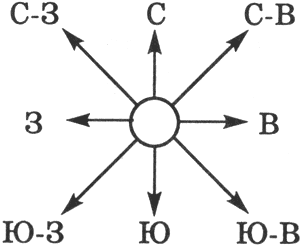 |
| Рис. 1.4. Управление роботом с использованием информационных сообщений |
Всего возможных информационных сообщений 8, поэтому формула (1.1) принимает вид уравнения относительно I:
Разложим стоящее в левой части уравнения число 8 на сомножители и представим его в степенной форме:
Равенство левой и правой частей уравнения справедливо, если равны показатели степени числа 2. Таким образом, I = 3 бита, т. е. количество информации, которое несет роботу каждое информационное сообщение, равно 3 битам.
Алфавитный подход к определению количества информации
При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
 |
| Рис. 1.5. Передача информации |
Формула (1.1) связывает между собой количество возможных информационных сообщений N и количество информации I, которое несет полученное сообщение. Тогда в рассматриваемой ситуации N – это количество знаков в алфавите знаковой системы, а I – количество информации, которое несет каждый знак:
С помощью этой формулы можно, например, определить количество информации, которое несет знак в двоичной знаковой системе:
Таким образом, в двоичной знаковой системе знак несет 1 бит информации. Интересно, что сама единица измерения количества информации «бит» (bit) получила свое название ОТ английского словосочетания «Binary digiT» – «двоичная цифра».
Информационная емкость знака двоичной знаковой системы составляет 1 бит.
Чем большее количество знаков содержит алфавит знаковой системы, тем большее количество информации несет один знак. В качестве примера определим количество информации, которое несет буква русского алфавита. В русский алфавит входят 33 буквы, однако на практике часто для передачи сообщений используются только 32 буквы (исключается буква «ё»).
С помощью формулы (1.1) определим количество информации, которое несет буква русского алфавита:
Таким образом, буква русского алфавита несет 5 битов информации (при алфавитном подходе к измерению количества информации).
Количество информации, которое несет знак, зависит от вероятности его получения. Если получатель заранее точно знает, какой знак придет, то полученное количество информации будет равно 0. Наоборот, чем менее вероятно получение знака, тем больше его информационная емкость.
В русской письменной речи частота использования букв в тексте различна, так в среднем на 1000 знаков осмысленного текста приходится 200 букв «а» и в сто раз меньшее количество буквы «ф» (всего 2). Таким образом, с точки зрения теории информации, информационная емкость знаков русского алфавита различна (у буквы «а» она наименьшая, а у буквы «ф» – наибольшая).
Количество информации в сообщении. Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Если знаки несут одинаковое количество информации, то количество информации Ic в сообщении можно подсчитать, умножив количество информации Iз, которое несет один знак, на длину кода (количество знаков в сообщении) К:
Так, каждая цифра двоичного компьютерного кода несет информацию в 1 бит. Следовательно, две цифры несут информацию в 2 бита, три цифры – в 3 бита и т. д. Количество информации в битах равно количеству цифр двоичного компьютерного кода (табл. 1.1).
Все мы привыкли к тому, что все вокруг можно измерить. Мы можем определить массу посылки, длину стола, скорость движения автомобиля. Но как определить количество информации, содержащееся в сообщении? Ответ на вопрос в статье.
Итак, давайте для начала выберем сообщение. Пусть это будет «Принтер — устройство вывода информации.«. Наша задача — определить, сколько информации содержится в данном сообщении. Иными словами — сколько памяти потребуется для его хранения.
Определение количества информации в сообщении
Для решения задачи нам нужно определить, сколько информации несет один символ сообщения, а потом умножить это значение на количество символов. И если количество символов мы можем посчитать, то вес символа нужно вычислить. Для этого посчитаем количество различных символов в сообщении. Напомню, что знаки препинания, пробел — это тоже символы. Кроме того, если в сообщении встречается одна и та же строчная и прописная буква — мы считаем их как два различных символа. Приступим.
В слове Принтер 6 различных символов (р встречается дважды и считается один раз), далее 7-й символ пробел и девятый — тире. Так как пробел уже был, то после тире мы его не считаем. В слове устройство 10 символов, но различных — 7, так как буквы с, т и о повторяются. Кроме того буквы т и р уже была в слове Принтер. Так что получается, что в слове устройство 5 различных символов. Считая таким образом дальше мы получим, что в сообщении 20 различных символов.
Далее вспомним формулу, которую называют главной формулой информатики:
Подставив в нее вместо N количество различных символов, мы узнаем, сколько информации несет один символ в битах. В нашем случае формула будет выглядеть так:
Вспомним степени двойки и поймем, что i находится в диапазоне от 4 до 5 (так как 2 4 =16, а 2 5 =32). А так как бит — минимальная единица измерения информации и дробным быть не может, то мы округляем i в большую сторону до 5. Иначе, если принять, что i=4, мы смогли бы закодировать только 2 4 =16 символов, а у нас их 20. Поэтому получаем, что i=5, то есть каждый символ в нашем сообщении несет 5 бит информации.
Осталось посчитать сколько символов в нашем сообщении. Но теперь мы будем считать все символы, не важно повторяются они или нет. Получим, что сообщение состоит из 39 символов. А так как каждый символ — это 5 бит информации, то, умножив 5 на 39 мы получим:
5 бит x 39 символов = 195 бит
Это и есть ответ на вопрос задачи — в сообщении 195 бит информации. И, подводя итог, можно написать алгоритм нахождения объема информации в сообщении:
Объемный способ измерения информации
Технический способ измерения количества информации (или, точнее, информационного объема сообщения) основан на подсчета количества символов, из которых образовано сообщение. При этом не учитывается смысловое содержание сообщения. Например, многократное повторение одного и того же текста не несет новой информации, однако в результате занимает больший объем памяти, требует большего времени для передачи и т.п. Поэтому этот способ удобен в технических расчетах.
Американский математик и инженер К. Шеннон в 1948 г. получил формулу для расчета количества информации, содержащейся в системе, обладающей произвольным набором неравновероятных (в общем случае) состояний
где n – число возможных состояний системы, pi – вероятность i-го состояния (причем pi = 1)
Чем меньше вероятность наступления события, тем большую информацию это событие несет.
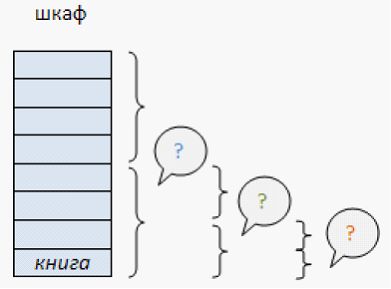
На книжном стеллаже восемь полок. Книга может быть поставлена на любую из них. Сколько информации содержит сообщение о том, где находится книга?
Применим метод половинного деления. Зададим несколько вопросов уменьшающих неопределенность знаний в два раза.
– Книга лежит выше четвертой полки?
Книга — на второй полке?
Ну теперь все ясно! Книга лежит на первой полке! Каждый ответ уменьшал неопределенность в два раза.
Всего было задано три вопроса. Значит набрано 3 бита информации. И если бы сразу было сказано, что книга лежит на первой полке, то этим сообщением были бы переданы те же 3 бита информации.
Если обозначить возможное количество событий, или, другими словами, неопределенность знаний N, а буквой I количество информации в сообщении о том, что произошло одно из N событий, то можно записать формулу:
Количество информации, содержащееся в сообщении о том, что произошло одно из N равновероятных событий, определяется из решения показательного уравнения:
А теперь познакомимся с другим способом измерения информации. Этот способ не связывает количество информации с содержанием сообщения, и называется он алфавитным подходом.
При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.
Полное количество символов алфавита принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и отмеченных дополнительных символов равна 54.
В каждой очередной позиции текста может появиться любой из N символов. Тогда, согласно известной нам формуле, каждый такой символ несет I бит информации, которое можно определить из решения уравнения: 2I = 54. Получаем: I = 5.755 бит.
Вот сколько информации несет один символ в русском тексте! А теперь для того, чтобы найти количество информации во всем тексте, нужно посчитать число символов в нем и умножить на I.
Посчитаем количество информации на одной странице книги. Пусть страница содержит 50 строк. В каждой строке — 60 символов. Значит, на странице умещается 50×60=3000 знаков. Тогда объем информации будет равен: 5,755 х 3000 = 17265 бит.
При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита.
Пусть небольшая книжка, сделанная с помощью компьютера, содержит 150 страниц; на каждой странице — 40 строк, в каждой строке — 60 символов. Значит страница содержит 40×60=2400 байт информации. Объем всей информации в книге: 2400 х 150 = 360 000 байт.
В любой системе единиц измерения существуют основные единицы и производные от них.
Для измерения больших объемов информации используются следующие производные от байта единицы:
1 килобайт = 1Кб = 210 байт = 1024 байта.
1 мегабайт = 1Мб = 210 Кб = 1024 Кб.
1 гигабайт = 1Гб = 210 Мб = 1024 Мб.
Прием-передача информации могут происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации или скорость информационного потока.
Очевидно, эта скорость выражается в таких единицах, как бит в секунду (бит/с), байт в секунду (байт/с), килобайт в секунду (Кбайт/с) и т.д.
Вопросы для самопроверки
Вопросы для самопроверки
1. Формальная и неформальная постановка задачи.
2. Дайте определение «модель» и требования к моделированию.
3. Характеристика стадий построения информационной модели.
4. Классификация моделей.
5. Виды форм представления информационных моделей.
6. Этапы разработки компьютерных моделей.
7. Информация, классификация информации.
8. Методы получения и использования информации.
9. Носитель информации.
10. Способы измерения информации.
11. Алфавитный подход к измерения информации.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8956 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно