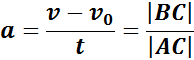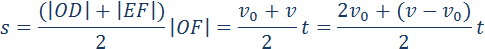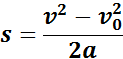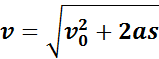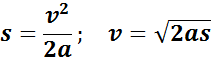Чем больше скорость тем больше ускорение

Ускорение при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

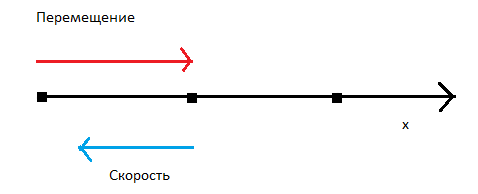
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

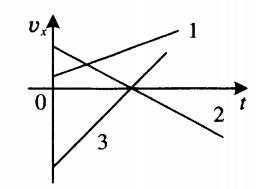
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

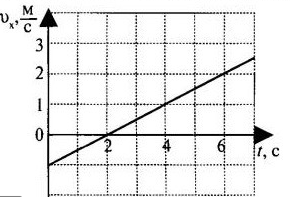
Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Скорость при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Описывая движение с постоянной скоростью, мы могли с уверенностью сказать, какую скорость имеет тело в любой момент времени. В случае с равноускоренным движением это не так, потому что скорость постоянно меняется. Поэтому для его описания вводится понятие мгновенной скорости.

Скорость тела в момент времени t равна сумме начальной скорости тела в момент времени t₀ и произведения ускорения этого тела на время t, в течение которого это тело двигалось. В векторном виде это записывается так:

v — скорость тела в данный момент времени, v ₀ —скорость тела в начальный момент времени, a — ускорение тела, t — время, в течение которого это тело двигалось

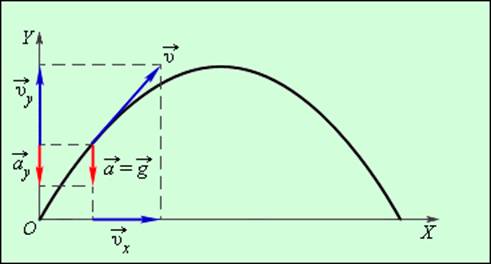
Направление вектора скорости при равномерном равноускоренном движении не всегда совпадает с направлением вектора ускорения и вектором перемещения тела.

Пример №1. Мальчик пробежал 200 метров по прямой линии, а затем вернулся в исходное положение. Определить направление вектора скорости и перемещения в момент, когда мальчик, возвращаясь в исходное положение, находился на полпути до него.

Началу вектора перемещения соответствует исходное положение мальчика. Когда мальчик возвращался и находился на полпути до исходного положения, концу вектора его перемещения соответствовала точка, лежащая посередине 200-метрового отрезка. Поэтому вектор перемещения направлен в сторону ОХ. Но мальчик в это время направлялся в обратную сторону. Поэтому его скорость была направлена против направления оси ОХ.

Скалярная формула скорости

В случае равноускоренного прямолинейного движения можно вместо векторов использовать скаляры. Тогда формула примет следующий вид:

Знак «+» ставится в случае, когда тело разгоняется, знак «–» — когда оно тормозит.

Проекция скорости

Проекция скорости при равноускоренном прямолинейном движении имеет вид:

Знак проекции скорости зависит от того, в какую сторону движется тело:

Знак проекции скорости не зависит от того, каким является движение: равнозамедленным или равноускоренным.

График скорости

График скорости — график зависимости проекции скорости от времени. Графиком скорости при равноускоренном прямолинейном движении является прямая.

Сравнение модулей ускорения по графикам скоростей

Чтобы сравнить модули ускорений по графикам скоростей, нужно сравнить их углы наклона к оси времени. Чем больше между ними угол, тем больше модуль ускорения. Так, на рисунке выше большим модулем ускорения обладает тело 3 — угол между его графиком скорости и осью времени максимальный. Меньшим модулем ускорения обладает тело 1, так как угол между его графиком скорости и осью времени минимальный.

Пример №2. Ниже представлен график движения велосипедиста. Опишем характер его движения на участке от 0 до 2 с, в момент времени t=2 с и на участке от 2 с.

На отрезке пути от 0 до 2 с велосипедист двигался в направлении, противоположном оси ОХ. При этом модуль его скорости уменьшался. В момент времени t=2 c велосипедист приостановился и поменял направление движения, и дальше оно стало совпадать с осью ОХ. Модуль его скорости при этом начал расти. Но на всем пути независимо от направления движения велосипедиста вектор его ускорения всегда был направлен в сторону ОХ. Однако до 2 с движение считалось равнозамедленным, так как ускорение и скорость были направлены в противоположные стороны. После 2 с движение стало равноускоренным, так как направления скорости и ускорения совпали.

Пример №3. Грузовик ехал с некоторой постоянной скоростью. Затем он затормозил и остановился в течение 5 секунд. Найти постоянную скорость, с которой двигался грузовик, если при торможении модуль его ускорения составил 2 м/с.

Так как движение равнозамедленное, в формуле будем использовать» знак «–». Он будет указывать на то, что скорость грузовика с течением времени уменьшалась:

Выразим начальную скорость:

Так как грузовик в итоге остановился, его конечная скорость равна 0. Подставляем известные данные в формулу и получаем:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Источник

Второй закон Ньютона (Расчёты Примеры)

Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.

В результате чего были выведена новая формула второго закона ньютона а = F /m,

Что такое второй закон Ньютона, масса и вес тела

Обобщая результаты опытов Галилея по падению тяжелых тел, астрономические законы Кеплера о движении планет, данные собственных исследований.

Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.

Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.

Ускорение от величины силы

I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.

Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at₂) : 2 определим ускорение a.

Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку

Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m . Это отношение назовем массой тела.

Зависимость ускорения от массы

II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).

Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть

Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).

Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):

где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.

Результирующая сила F равна векторной сумме всех сил, приложенных к телу;

Следовательно, сила равна произведению массы на ускорение.

Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение

подставим это выражение в уравнение второго закона Ньютона. Получим

Что такое импульс

Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (т υ ).

Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)

Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содер жащегося в данной теле. Это определение несовершенно.

Из второго закона Ньютона вытекает следующее определение массы. Из равенства

видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость это го тела и наоборот.

Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.

Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:

где m — масса тела, движущегося со скоростью υ; m₀ — масса этого же тела, находящегося в покое; с = 3 • 10 8 м/с скорость света в вакууме.

Проанализируем данное уравнение:

По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.

Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.

Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.

Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.

Масса тела с ростом скорости

Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.

Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.

Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже).

Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ₀ = 0) называется свободным падением.

Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.

Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.

Если Р — сила тяжести, m — масса, g — ус корение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м /с 2 ), то применяя второй закон динамики, получим

Выразим с помощью этой формулы веса двух различных тел. Тогда:

Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.

Задачи на второй закон ньютона

Дано:
m = 1000 кг
a = 1 м/с 2

Решение:

Запишем второй закон Ньютона :

F = 1000 кг • 1 м/с 2 = 1000 Н

Ответ: 1000 Н.

2. На мяч действует сила F = 70 Н, масса мяча m = 0,2 кг, найти его ускорение a.

Дано:

Найти:

Решение:

Запишем второй закон Ньютона :

Статья на тему Второй закон Ньютона

Похожие страницы:

Понравилась статья поделись ей

Источник

Равноускоренное движение

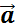
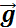
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. Примером такого движения является движение камня, брошенного под некоторым углом к горизонту (без учета сопротивления воздуха). В любой точке траектории ускорение камня равно ускорению свободного падения . Для кинематического описания движения камня систему координат удобно выбрать так, чтобы одна из осей, например ось OY, была направлена параллельно вектору ускорения. Тогда криволинейное движение камня можно представить как сумму двух движений – прямолинейного равноускоренного движения вдоль оси OY и равномерного прямолинейного движения в перпендикулярном направлении, т. е. вдоль оси OX (рис. 1.4.1).

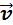
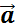
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости и ускорения направлены вдоль прямой движения. Поэтому скорость υ и ускорение a в проекциях на направление движения можно рассматривать как алгебраические величины.

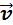
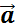
Проекции векторов скорости и ускорения на координатные оси. ax = 0, ay = –g

При равноускоренном прямолинейном движении скорость тела определяется формулой

(*)

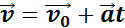
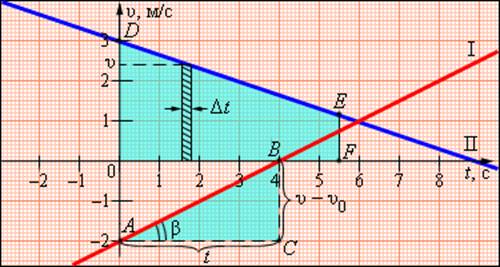
В этой формуле υ₀ – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).

Графики скорости равноускоренного движения

По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC:

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика II: υ₀ = 3 м/с, a = –1/3 м/с 2

График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.

Так как υ – υ₀ = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

(**)

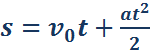
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y₀ прибавить перемещение за время t:

(***)

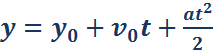
Это выражение называют законом равноускоренного движения.

При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ₀ и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде

Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ₀, ускорение a и перемещение s:

Если начальная скорость υ₀ равна нулю, эти формулы принимают вид

Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ₀, υ, s, a, y₀ являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.

Источник