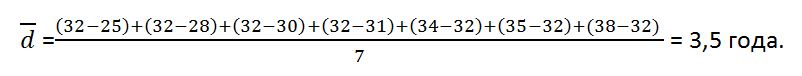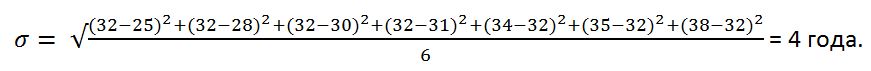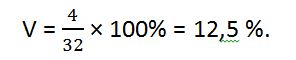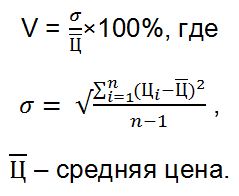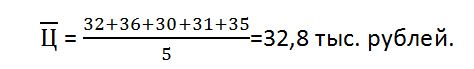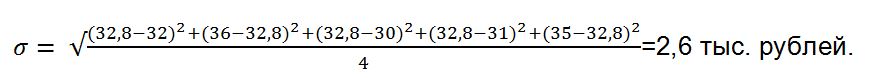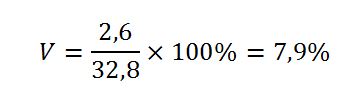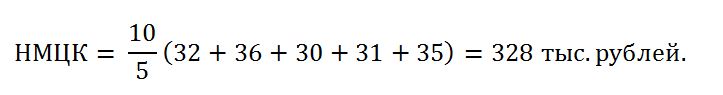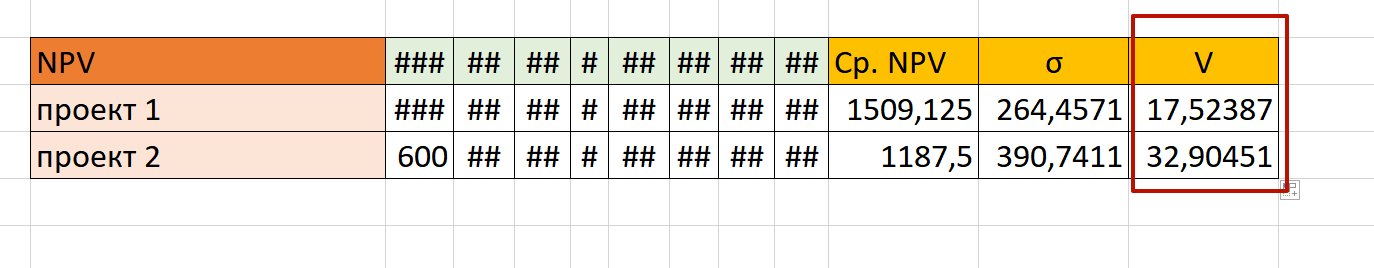Чем больше величина коэффициента вариации

Коэффициент вариации по 44-ФЗ

Понятие

Коэффициент вариации по 44-ФЗ — это показатель разброса по выбранным ценовым предложениям тендера, применяемый при использовании метода сопоставимых рыночных цен.

Он необходим для определения степени неоднородности полученных цен, так как его значение показывает, какую долю занимает средний разброс от среднего значения.

Коэффициент вариации был введён Приказом Минэкономразвития № 567. Приказ также содержит методические рекомендации по его оптимальным показателям.

Значения

Коэффициент может принимать четыре промежутка, от которых зависит возможность использования исследования рынка:

Допустимым вариантом коэффициента вариаций по 44-ФЗ является результат до 33%.

При результате свыше 33% заказчику необходимо сделать новую выборку поставщиков для определения НМЦК.

Использование неоднородных результатов не допускается, а проведённое исследование рынка признаётся недействительным.

В том случае, когда по каким-то причинам запросить другие данные о стоимости на интересующие товары, работы или услуги невозможно, заказчик может воспользоваться сведениями из реестра контрактов.

Расчёт

Коэффициент вариации рассчитывается по формуле:

(Среднеквадратичное отклонение/Средняя стоимость) * 100%

Первая переменная считается следующим образом:

(√∑_i=1 n (Цена — Средняя арифметическая цена) 2 )/n — 1, где n — это количество предложений.

При наличии в одной закупке нескольких товаров коэффициент определяется в отношении каждого из них.

От правильного определения коэффициента зависит правильный расчёт НМЦК, поэтому тщательно проверяйте полученные результаты и следите за соответствием допустимым значениям.

Источник

Тема 9 Показатели вариации

Показатели вариации в анализе взаимосвязей

Для измерения степени колеблемости отдельных значений признака относительно средней исчисляют основные показатели вариации.

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для полного анализа изучаемого процесса или явления. Иногда совершенно непохожие по своему внутреннему строению совокупности могут иметь равные средние величины. Поэтому для более детального изучения того или иного явления необходимо учитывать разброс или вариацию значений отдельных единиц совокупности. Измерение вариации признаков имеет как теоретическое, так и практическое значение.

Так, например, для выявления наиболее стабильно работающего коллектива или предприятия наравне с другими показателями рассчитывают и основные показатели вариации. Эти показатели дают возможность количественно определить размеры устойчивости производительности труда, уровня квалификации, цен на основные виды выпускаемой продукции и т.п. Измерение размеров вариации такого показателя, как «выполнение работ в срок» имеет важное значение для принятия решений заказчиками и инвесторами, т.к. ситуация, в которой присутствует изменчивость признака, часто содержит риск. Осо­бое значение показатели вариации приобретают в анализе рынка ценных бумаг, где мера колеблемости отождествляется с мерой рискованности вложения денежных средств.

Основными показателями, характеризующими вариацию, являются:

1) Размах вариации

2) Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений:

где –абсолютные значения отклонений отдельных вариантов xi от средней арифметической ; fi – частота.

3. Дисперсия – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической:

4. Среднее квадратическое отклонение – корень квадратный из дисперсии:

5. Коэффициент вариации – используется для сравнительной оценки вариации, а также для характеристики однородности совокупности:

Пример. Для иллюстрации расчетов воспользуемся данными нижеприведенной табл. 9.1:

Таблица 9.1 ‑ Данные о продаже основных марок холодильников:

Рассчитаем размах вариации.

R= 1200-460=740$

Пример вычисления размаха вариации

Размах вариации служит незаменимой мерой разброса экстремальных значений признака. Кроме характеристики границ разброса признака, размах вариации может быть использован для выявления ошибок. При наличии очень больших (или очень малых) ошибочно записанных значений признака размах вариации сразу резко возрастает, что требует проверки и корректировки исходных данных.

Недостатком данного показателя является то, что он оценивает только границы варьирующего признака и не отражает его колеблемость внутри этих границ. Вследствие этого размах вариации может неправильно характеризовать общую колеблемость признака.

Этого недостатка лишен другой показатель – дисперсия, рассчитываемый как средний квадрат отклонений значений признака от их средней величины.

Между индиви­дуальными отклонениями от средней и колеблемостью признака существует прямая зави­симость: чем сильнее колеблемость признака, тем больше отклонения его значений от средней величины и менее устойчив изучаемый показатель.

Как и средняя величина этот показатель может быть рассчитан в двух формах: взвешенной и невзвешенной

По приведенным выше данным определим средневзвешенную цену холодильника:

Далее рассчитаем дисперсию:

. Следует отметить, что дисперсия еще не дает представления об однородности со­вокупности, и этому показателю трудно дать экономическую интерпретацию, т.к. он рас­считан в квадратных единицах. Поэтому следующим шагом в исследовании однородности совокупности является расчет среднего квадратического отклонения, показывающего, на­сколько в среднем отклоняются конкретные варианты признака от его среднего значения. Оно определяется как квадратный корень из дисперсии и имеет ту же размерность что и изучаемый признак. .

Рассчитаем среднее квадратическое отклонение

Рассмотренные показатели позволяют получить абсолютное значение вариации признака. Однако для сравнения разных совокупностей с точки зрения устойчивости ка­кого-либо одного признака или для определения однородности совокупности рассчиты­вают относительные показатели.

Эти показатели вычисляются как отношение размаха вариации, среднего линейно­го отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего эти показатели выражаются в процентах.

Определим значение показателя вариации по вышеприведенным данным таблицы

Совокупность считается однородной, если V не превышает 33%.

Если V 25% – вариация сильная.

Вывод: Рассчитанная величина свидетельствует о неоднородности цен на холодильники, т.к. однородной совокупность считается, если коэффициент вариации меньше 33% (для распределений близких к нормальному).

!! Следует отметить, что коэффициент вариации может быть более 100%, что, в част­ности, может быть при наличии значений сильно отличающихся от средней величины. Такой результат означает, что в исследуемой совокупности сильна вариация признаков по отношению к средней величине.

Изучая вариацию интересующего нас признака в пределах исследуемой совокупно­сти и опираясь на общую среднюю в расчетах, трудно оценить степень воздействия на него какого-либо отдельного признака.

При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками – факторным (оказывающим влияние на взаимосвязанный с ним признак) и результативным (подвер­женным влиянию).

Для выявления взаимосвязи исходная совокупность делится по факторному признаку на группы. Выводы о степени взаимосвязи базируются на анализе вариации резуль­тативного признака. Если статистическая совокупность разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих вариацию индиви­дуальных значений признака, используют правило сложения дисперсий.

Общая дисперсия представляет собой сумму средней из виутригрупповой и меж­групповой и дисперсий:

Общая дисперсия характеризует вариацию признака по всей совокупности как ре­зультат влияния всех факторов, определяющих индивидуальные различия единиц сово­купности.

Межгрупповая дисперсия характеризует вариацию, обусловленную влиянием фактора, положенного в основу группировки.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результа­тивного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка. Другими словами внутригрупповая дисперсия отражает случайную вариацию. Внутригрупповая дисперсия рас­считывается отдельно по каждой j-ой группе.

Для всех групп в целом вычисляется средняя из внутригрупповых дисперсий, взвешенных на частоты соответствующих групп по формуле:

Взаимосвязь между тремя видами дисперсий получила название правила сложения дисперсий. Таким образом, зная два вида дисперсий всегда можно определить третий:

Из этого равенства следует, что общая дисперсия, как правило, будет больше средней из групповых дисперсий. Это обусловлено тем, что при расчленении об­щей совокупности единиц на части по какому-либо признаку образуются более или менее однородные группы, в результате чего сокращается колеблемость признаков в пределах каждой группы. Это приводит к тому, что средняя из групповых дисперсий оказывается меньше дисперсии признака по всей совокупности единиц, причем разница между этими показателями будет тем больше, чем однороднее получаются группы в результате расчле­нения общей совокупности.

Теснота связи между факторным и результативным признаками оценивается на ос­нове эмпирического корреляционного отношения:

Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.

Пример. На следующем условном примере исследуем зависимость объема выполненных ра­бот от формы собственности проектно-изыскательских организаций.

Таблица 9.2. Выполнение работ проектно-изыскательскими организациями разной формы собственности

Объем выполненных работ

Форма собственности	Количество предприятий	Итого
Государственная	4	10,30,20,40	100
Негосударственная	6	20, 40, 60, 20, 50, 50	240
Итого	10	340

1) Определим средний объем работ для предприятий двух форм собственности.

2) Определим средний объем работ для каждой формы собственности.

3) Рассчитаем общую и внутригрупповые (т.е. для каждой группы) дисперсии.

4) Определим среднюю из внутригрупповых и межгрупповую дисперсию. Для этого полученные ранее данные заносятся в таблицу расчета.

Таблица 9.3. – Вспомогательная таблица

Государственная425125Негосударственная640233Итого10

Пример. Средняя из внутригрупповых дисперсий

Пример. Межгрупповая дисперсия

На последнем этапе решения задачи необходимо проверить тождество, отражающее закон сложения дисперсий:

Проверка закона сложения дисперсий: 54,0+189,8=243,8

Вывод: Таким образом, можно сделать вывод о том, что объем работ, выполненных проектно-изыскательскими организациями на 22% [(54,0/243,8) х 100%] зависит от фак­тора, положенного в основание группировки, т.е. от формы собственности, а на 78% [(189,8/243,8)х100%)] ‑ от прочих факторов.

Вывод о том, что объем выполненных работ в гораздо большей степени зависит от каких-либо других факторов, чем от формы собственности предприятий подтверждается и величиной эмпирического корреляционного отношения:

Вывод: Величина этого показателя свидетельствует о том, что зависимость объема работ от формы собственности предприятия невелика

Контрольные задания

Вычислить: а) размах вариации; б)среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; относительные показатели вариации возраста студентов.

2. По данным статистических ежегодников постройте таблицу с рядом показателей и определите показатели вариации: а) размах; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) коэффициент вариации. Оцените количественную однородность совокупности.

Источник

Что такое коэффициент вариации и для чего он нужен

Коэффициент вариации – это статистический показатель, какой широко используется в финансовых расчетах. Он показывает степень разброса значений в числовой последовательности. А именно, насколько любая из величин отклоняется от средней. Если вариация слишком высока, то оценивать среднее значение некорректно. В этой ситуации обыкновенно исключают минимальное и максимальное число.

Показатель чаще всего применяется при формировании начальной минимальной цены контракта по 44-ФЗ. Она должна опираться на выборке рыночных цен, а в их оценке как раз и используется вариация. Кроме того, применяется при анализе рисков инвестиционных проектов и доходности ценных бумаг. В цельном, показатели вариации применимы в любой сфере, где требуется оценить совокупность данных и их разнообразие: статистика, математика, экономический разбор, социология, маркетинг и т.д.

Формулы расчета в статистике

Для оценки совокупности значений и их однородности применяют следующие инструменты:

Рассмотрим применение указанных формул на примере оценки среднего возраста трудящихся в отделе кадров. В указанном подразделении трудятся 7 сотрудников, которым 25, 28, 30, 31, 34, 35 и 38 лет. Размах вариации покажет нам разницу в году между самым младшим и самым старшим из них:

Рассчитаем среднее линейное отклонение. Для этого для начала найдем посредственный возраст в отделе: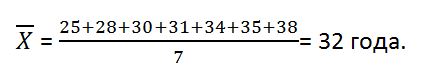Теперь посчитаем среднее линейное отклонение:

Соответственно, мы можем сказать, что средний возраст сотрудников составляет 32 ± 3,5 года.

Среднеквадратичное отклонение покажет то же самое, но немало точно:

Коэффициент вариации покажет, на сколько процентов возраст каждого работника отличается от среднего по отделу:

Оценка коэффициента вариации

Если со посредственными значениями и отклонениями от них все понятно, то зачем же рассчитывается коэффициент вариации? С его помощью можно судить, насколько показательно усредненное смысл и можно ли по нему судить о выборке в целом. В нашем примере он позволит ответить на вопрос, можно ли утверждать то, что посредственный возраст по отделу кадров составляет 32 года. Либо реальные показатели будут слишком сильно выделяться от полученного значения?

В статистике определены следующие критерии оценки:

Если показатель вариации превышает 33%, то выборка почитается неоднородной и судить о ней по средним значениям никак нельзя. При незначительном разбросе достоверность средних будет максимальной. В нашем образце вариативность средняя и в целом оценивать возраст по средним значениям с учетом отклонений вполне можно.

Если посмотреть на числовой ряд, то видать, что только 2 сотрудника существенно отклоняются от среднего возраста. На практике при слишком высокой вариативности из анализа исключают максимальное и минимальное смыслы, после чего проводят повторную проверку. Также часто по коэффициенту вариации сравнивают разные выборки. В нашем образце это слабо применимо, но, например, при анализе цен конкурентов будет вполне эффективно для выбора наиболее подходящей для анализа совокупности смыслов.

Читайте также! Выплата дивидендов учредителям ООО и АО в 2019 году

Применение при закупках по 44-ФЗ

Федеральный закон 44-ФЗ регулирует распорядок проведения государственных закупок. Его цель – не допустить злоупотреблений должностных лиц и передачу контрактов «своим» фирмам по завышенным/заниженным стоимостям. Именно для этого в законе определен порядок того, как устанавливается начальная минимальная цена контракта (НМЦК) – та, с какой и будут начинаться торги.

Методика определения начальной минимальной цены

Законом предусмотрено 5 методов определения НМЦК:

При этом наиболее предпочтительным и рекомендуемым является именно первоначальный. Его суть в том, что анализируются цены точно таких же товаров или услуг (идентичных) либо при их отсутствии схожих (однородных). Оба понятия четко установлены:

Данный порядок определен статьей 22 вышеуказанного закона. В 2019 году в нее было привнесено несколько изменений:

Как рассчитать НМЦК

Для расчета начальной цены заказчику необходимо составить выборку рыночных цен. Это можно сделать вытекающими способами:

Обычно используется первый способ. Нескольким поставщикам отправляются запросы введённой формы, а на основании полученных ответов и осуществляются расчеты по следующей формуле:

Коэффициент вариации в данном случае предзнаменований вид:

Пример расчета

Рассмотрим, как рассчитать НМЦК и коэффициент вариации на примере закупки 10 холодильников для больницы. От 5 поставщиков бывальщины получены коммерческие предложения со следующими ценами: 32, 36, 30, 31 и 35 тыс. рублей за штуку.

Оценим однородность ценовых предложений линией расчета коэффициента вариации. Для начала рассчитаем среднюю цену:

Теперь необходимо найти среднеквадратичное отклонение:

И, наконец, рассчитываем коэффициент вариации:

V меньше 10%, таким манером, делаем вывод о том, что выборка однородна и ее можно использовать для установки закупочных цен для торгов.

Посчитаем минимальную цену контракта:

Использование в оценке рисков

В финансовом разборе степень отклонения показателя от среднего значения показывает уровень риска. Например, если прибыль в разные годы существования компании то существенно всходит, то падает в убыток, инвестировать в нее опасно. То же самое касается ценных бумаг и любых других биржевых инструментов. Самыми привлекательными будут стабильные бумаги с минимальными колебаниями котировок при неплохом росте. Таким образом, есть еще два направления, где активно используется коэффициент вариации: оценка рисков проекта и рисков по доходности ценных бумаг.

Декламируйте также! Организация и внедрение бережливого производства на предприятии

Инвестиционные проекты

Как правило, при оценке рисков инвестиционных проектов используются:

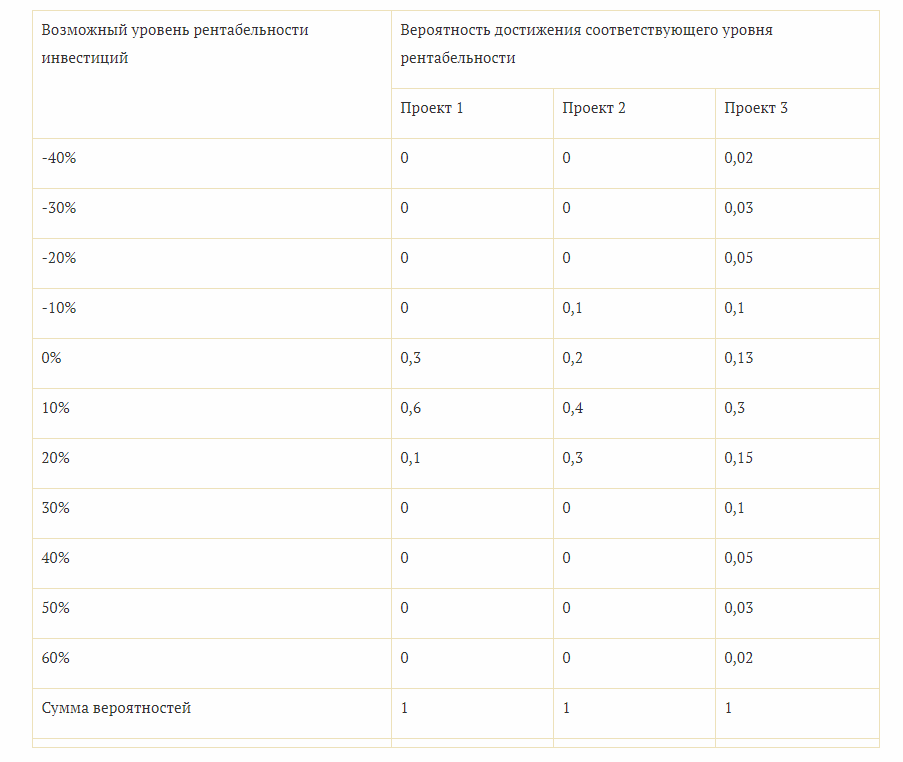
Обычно сравниваются несколько проектов по всем критериям. Также есть вариант рассмотреть возможность достижения того или другого уровня рентабельности:

В данном случае все проекты будут рискованными, поскольку коэффициент вариации составит 65%, 95% и 198% соответственно. Но риск по первому немало чем в 2 раза ниже, чем по третьему, поэтому из представленных вариантов лучше выбрать его.

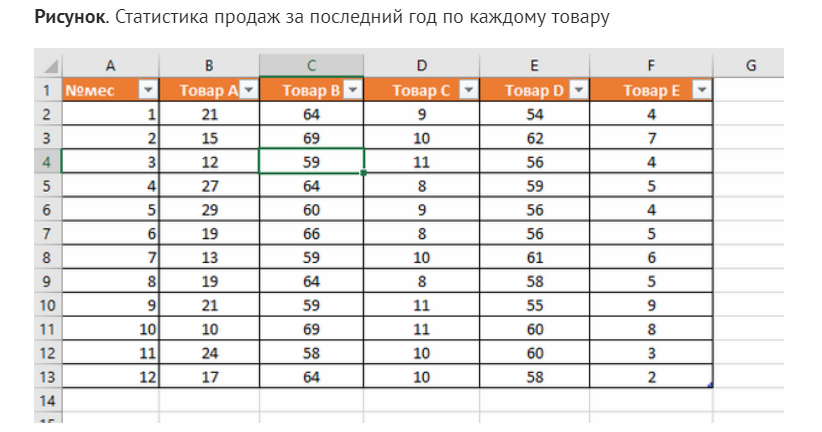
Нередко используют коэффициент при анализе спроса и принятии решении о закупках. Так, анализируется статистика продаж товара, после чего определяется, что закупать в первую очередь, а что только при наличии предзаказа:

В этом примере коэффициенты вариации по товарам А, B, C, D и E будут равны 30%, 6%, 12%, 4%, 38% соответственно. Очевидно, что спрос на продукцию E нестабилен и мощно колеблется в разные месяцы, поэтому заказывать целую партию рискованно.

Ценные бумаги

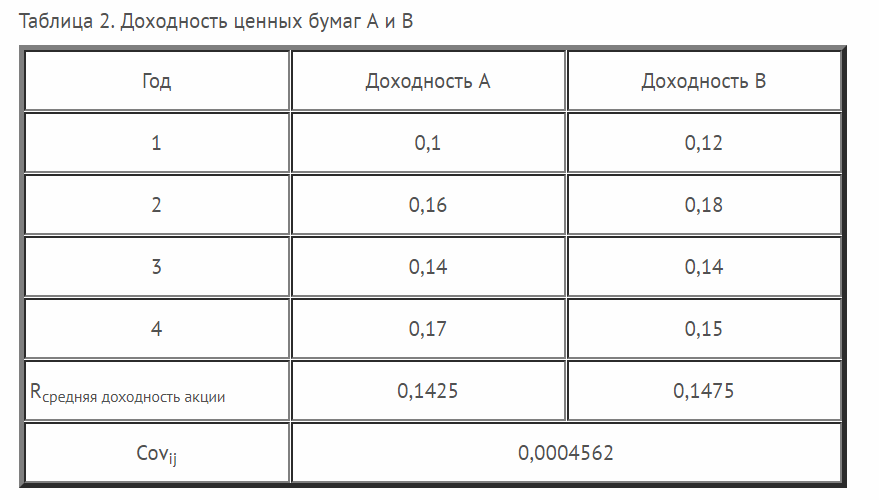
Что касается торговли на бирже, то тут можно оценивать в двух вариантах:

В первом случае, имея эти о колебаниях котировок в прошлом, мы сможем оценить риск вложения именно в данный инструмент. Во втором варианте можно оценить риск портфеля инвестиций на основании совокупности доходности любой его составляющей. Также риск портфеля можно проанализировать на основании совокупности вариаций каждой его составляющей во временном интервале. Все эти методики используются в комплексном анализе рисков инвестиционного портфеля.

Расчет в MS Excel

Как при расчете цены контракта, так и при оценке инвестиционных проектов выполнять громоздкие вычисления квадратичного отклонения и коэффициента вариации вручную весьма трудоемко. Поэтому рассмотрим, как быстро и просто выполнить это при помощи электронной таблицы Excel.

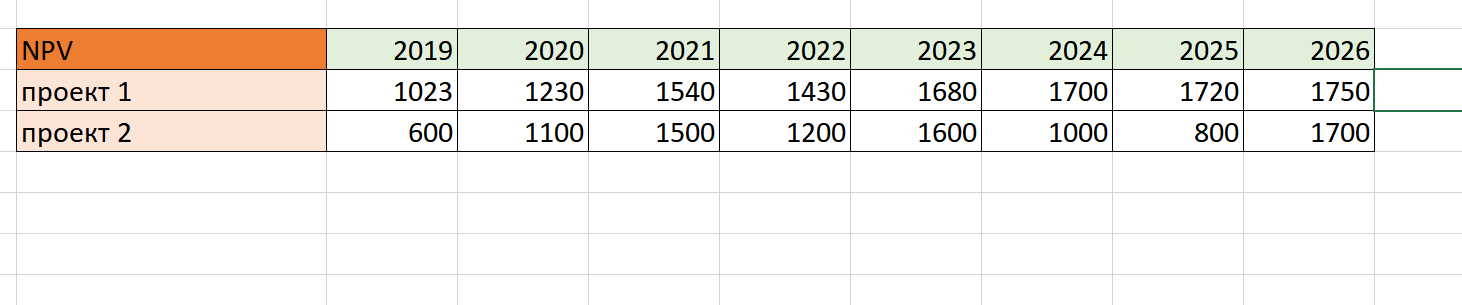
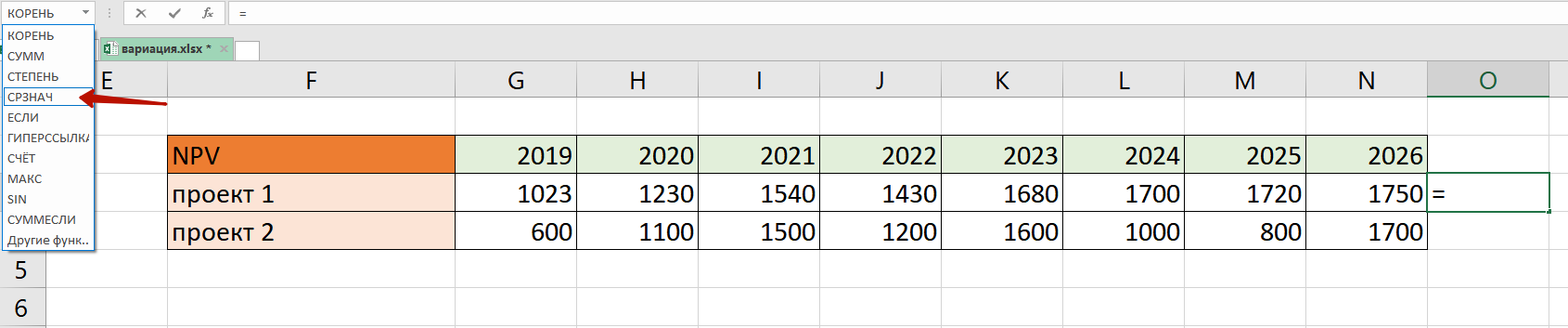
Для начала открываем редактор и создаем таблицу с отправными данными. Для примера возьмем два инвестиционных проекта с показателями NPV за 8 лет.

Далее находим среднее значение прибыли при помощи функции СРЗНАЧ:

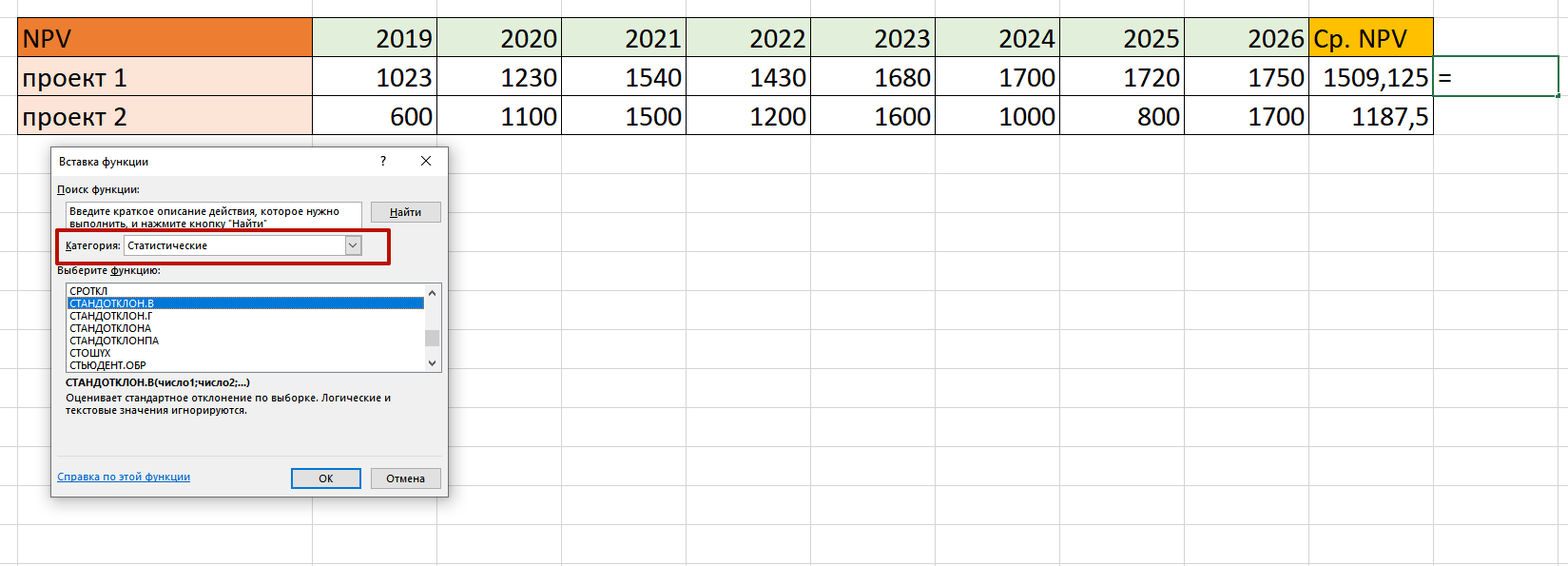
Вышли вот такие значения:

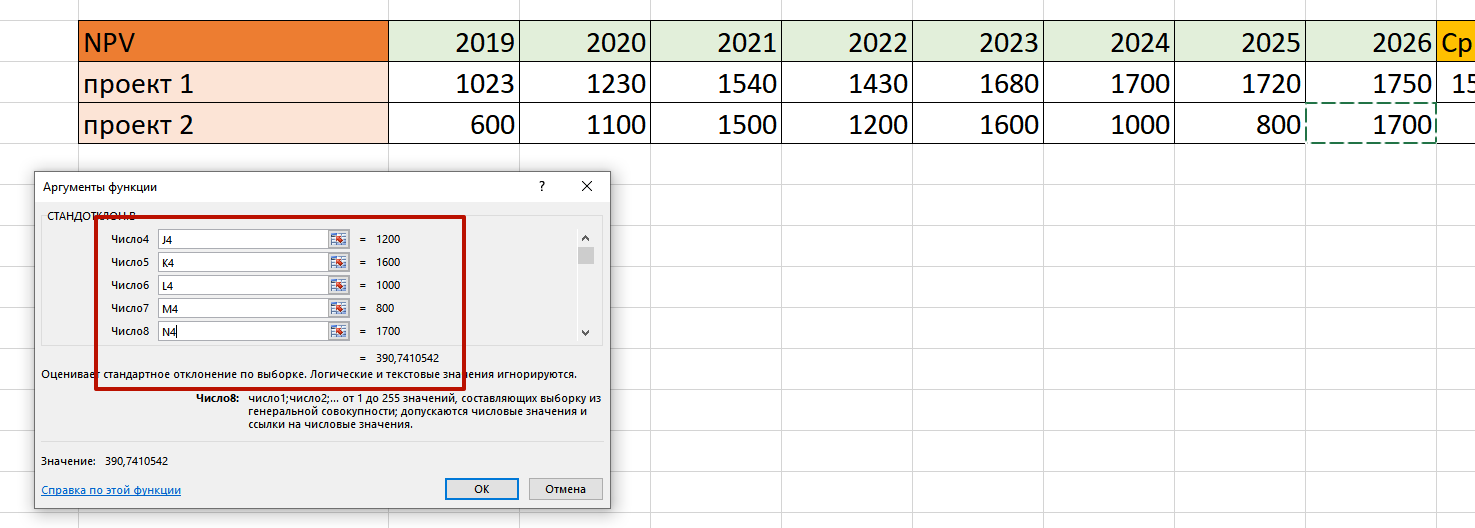
Теперь необходимо вычислить среднеквадратичное отклонение. Для этого предназначена функция СТАНДОТКЛОН.В

Обратите внимание, что в любую строку необходимо вбить одну ячейку, а не выбирать весь диапазон:

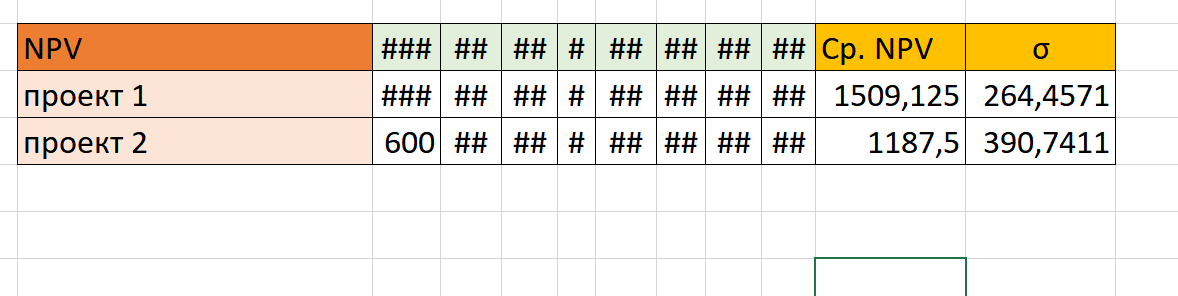
Таким образом, у нас есть рассчитанные посредственные значения доходности и среднеквадратичного отклонения по двум проектам:

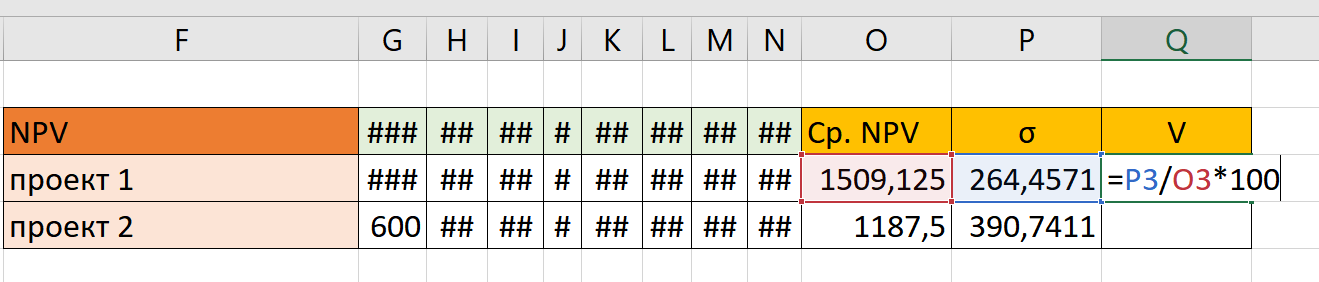
Теперь нам нужно найти коэффициент вариации. Для этого мы попросту вписываем вручную формулу: ячейку σ делим на среднюю доходность и умножаем на 100:

Таким образом, получаем следующие смыслы коэффициента вариации:

Можно сделать вывод о том, что первый проект менее рисковый, чем второй.

Источник