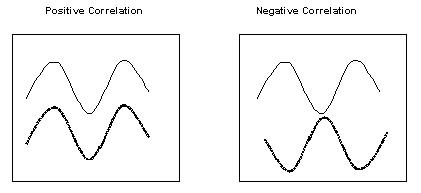
Чем выше корреляция тем лучше
Корреляции в дипломных работах по психологии
Термин «корреляция» активно используется в гуманитарных науках, медицине; часто мелькает в СМИ. Ключевую роль корреляции играют в психологии. В частности, расчет корреляций выступает важным этапом реализации эмпирического исследования при написании ВКР по психологии.
В этой статье мы простым языком объясним суть корреляционной связи, виды корреляций, способы расчета, особенности использования корреляции в психологических исследованиях, а также при написании дипломных работ по психологии.
Что такое корреляция
Корреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере.
Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше».
Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна).
Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект. Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие?
Правильно, между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная.
В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность.
Численное выражение корреляционной зависимости
Итак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение.
Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:
Прямая и обратная
Сильная и слабая
Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше.
Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов.
Испытуемый
Успеваемость (баллы)
Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет.
Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость между интеллектом и успеваемостью равна 1.
Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10).
Испытуемый
Успех в общении с противоположным полом (баллы)
Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет.
А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места.
Испытуемый
Длина прыжка с места (м)
Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0.
Мы рассмотрели крайние случаи. В реальных измерениях коэффициенты редко бывают равны точно 1 или 0. При этом принята следующая шкала:
Приведенная градация дает очень приблизительные оценки и в таком виде редко используются в исследованиях.
Чаще используются градации коэффициентов по уровням значимости. В этом случае реально полученный коэффициент может быть значимым или не значимым. Определить это можно, сравнив его значение с критическим значением коэффициента корреляции, взятым из специальной таблицы. Причем эти критические значения зависят от численности выборки (чем больше объем, тем ниже критическое значение).
Корреляционный анализ в психологии
Корреляционный метод выступает одним из основных в психологических исследованиях. И это не случайно, ведь психология стремится быть точной наукой. Получается ли?
В чем особенность законов в точных науках. Например, закон тяготения в физике действует без исключений: чем больше масса тела, тем сильнее оно притягивает другие тела. Этот физический закон отражает связь массы тела и силы притяжения.
Пример исследования на студентах из предыдущего раздела хорошо иллюстрирует использование корреляций в психологии:
Вот как могли выглядеть краткие выводы по результатам придуманного исследования на студентах:
Таким образом, уровень интеллекта студентов выступает позитивным фактором их академической успеваемости, в то же время негативно сказываясь на отношениях с противоположным полом и не оказывая значимого влияния на спортивные успехи, в частности, способность к прыгать с места.
Как видим, интеллект помогает студентам учиться, но мешает строить отношения с противоположным полом. При этом не влияет на их спортивные успехи.
Неоднозначное влияние интеллекта на личность и деятельность студентов отражает сложность этого феномена в структуре личностных особенностей и важность продолжения исследований в этом направлении. В частности, представляется важным провести анализ взаимосвязей интеллекта с психологическими особенностями и деятельностью студентов с учетом их пола.
Коэффициенты Пирсона и Спирмена
Рассмотрим два метода расчета.
Коэффициент Пирсона – это особый метод расчета взаимосвязи показателей между выраженностью численных значений в одной группе. Очень упрощенно он сводится к следующему:
Коэффициент ранговой корреляции Спирмена рассчитывается похожим образом:
В случае Пирсона расчет шел с использованием среднего значения. Следовательно, случайные выбросы данных (существенное отличие от среднего), например, из-за ошибки обработки или недостоверных ответов могут существенно исказить результат.
В случае Спирмена абсолютные значения данных не играют роли, так как учитывается только их взаимное расположение по отношению друг к другу (ранги). То есть, выбросы данных или другие неточности не окажут серьезного влияния на конечный результат.
Если результаты тестирования корректны, то различия коэффициентов Пирсона и Спирмена незначительны, при этом коэффициент Пирсона показывает более точное значение взаимосвязи данных.
Как рассчитать коэффициент корреляции
Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.
Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.
Расчет с помощью электронных таблиц Microsoft Excel
Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.
Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».
Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.
В таблицах Excel реализована формула расчета только коэффициента Пирсона.
Расчет с помощью программы STATISTICA
Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.
Как видно, расчет дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.
Использование корреляционного анализа в дипломных работах по психологии (пример)
Большинство тем выпускных квалификационных работ по психологии (дипломов, курсовых, магистерских) предполагают проведение корреляционного исследования (остальные связаны с выявлением различий психологических показателей в разных группах).
Сам термин «корреляция» в названиях тем звучит редко – он скрывается за следующими формулировками:
Рассмотрим кратко этапы его проведения при написании дипломной работы по психологии на тему: «Взаимосвязь личностной тревожности и агрессивности у подростков».
1. Для расчета необходимы сырые данные, в качестве которых обычно выступают результаты тестирования испытуемых. Они заносятся в сводную таблицу и помещаются в приложение. Эта таблица устроена следующим образом:
Asset Allocation: корреляция активов
Автор: Алексей Мартынов · Опубликовано 23.05.2016 · Обновлено 22.08.2016
В предыдущей статье мы говорили, что ребалансировка активов контролирует риск портфеля, а при удачном стечении обстоятельств может дать дополнительный выигрыш по доходности. Но это работает только в том случае, если активы в портфеле ведут себя по разному в одних и тех же условиях. Как найти такие активы, и как оценить их поведение между собой, вы узнаете из этой статьи.
В портфель должны включаться слабо взаимосвязанные активы, цена которых ведет себя по разному в одинаковых условиях. Это снижает риск портфеля и создает портфельный эффект. Связь разных активов между собой можно оценить математически с помощью корреляции. Корреляция показывает в какой степени динамика стоимости одного актива соотносится с динамикой другого актива.
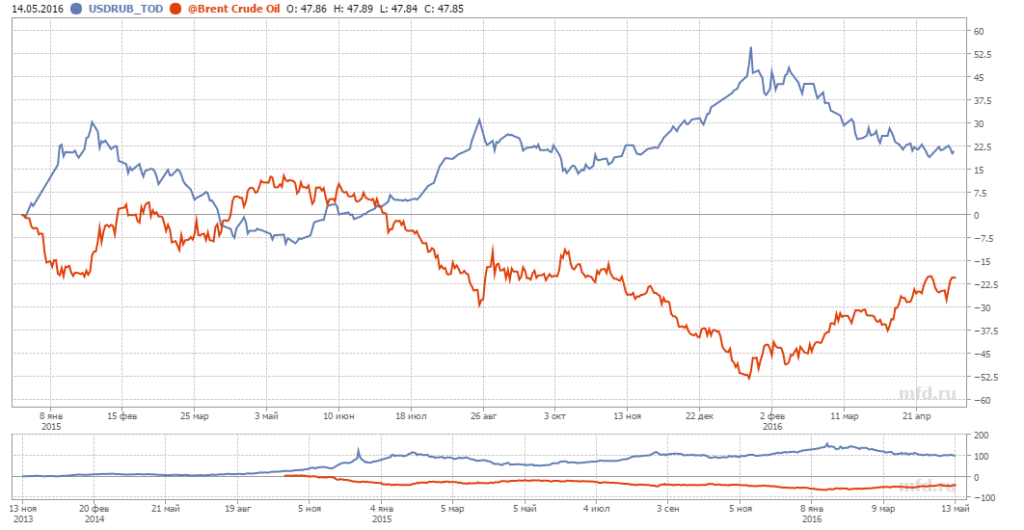
Из реальной жизни пример негативной корреляции можно найти в динамике курса доллара и цен на нефть в 2015-16 годах: когда нефть падала, курс доллара рос.
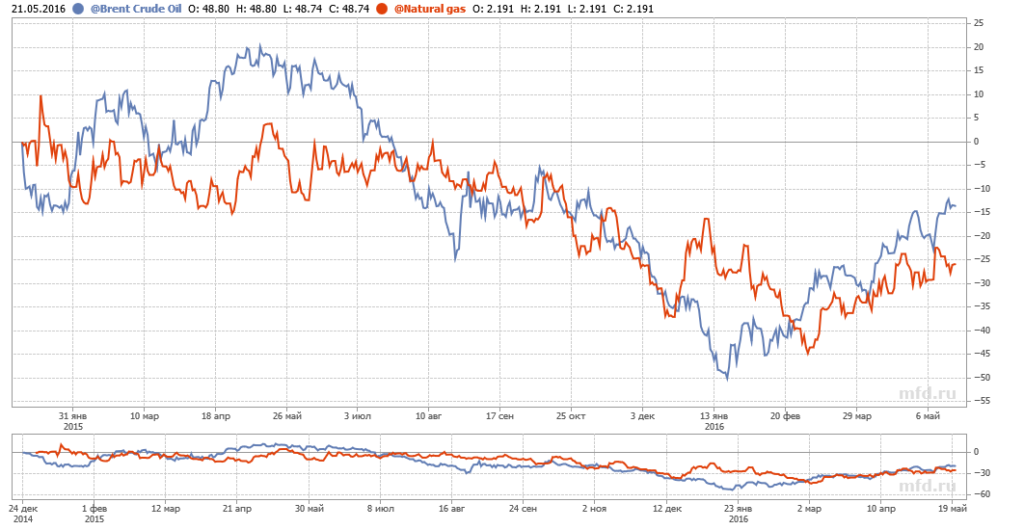
Положительная корреляция есть между ценами на нефть и натуральный газ: их цены двигаются схожим образом.
Влияние корреляции на риск портфеля
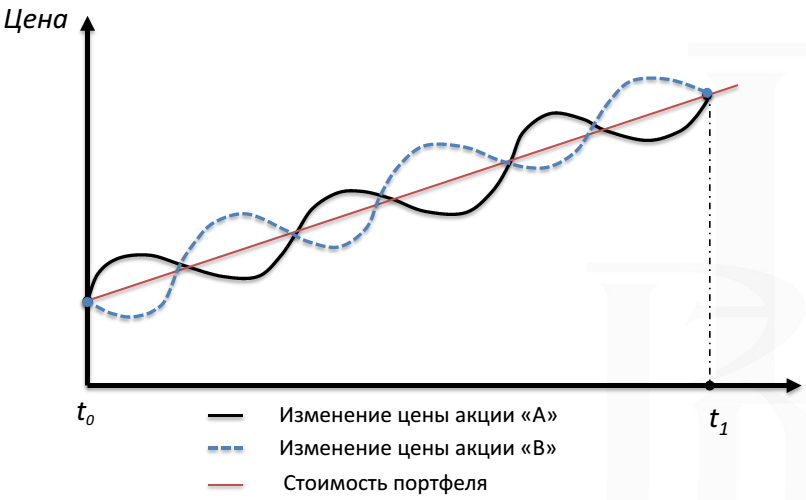
Поведение активов влияет на риск портфеля. Например, на картинке ниже изображены две акции, стоимость которых изменяется противоположно: когда одна растет, другая падает. Корреляция таких акций будет отрицательной. Если портфель будет состоять поровну их этих акций, то его стоимость будет изменяться гораздо плавнее по сравнению с каждой акцией в отдельности, то есть риск портфеля будет ниже, чем риск составляющих его акций. Это конечно идеализированная модель, но она наглядно показывает, как отрицательная корреляция активов снижает риск портфеля.
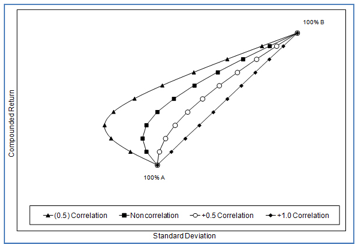
Теперь посмотрим, как корреляция может влиять на риск и доходность портфеля. На графике ниже изображена так называемая граница эффективности портфеля, состоящего из двух активов — А и В. Вертикальная ось — доходность портфеля, горизонтальная ось — стандартное отклонение доходности. Каждая линия представляет собой портфель с разной степенью корреляции активов (-0.5, 0.0, +0.5 и +1.0). Каждая точка на линии — это разные пропорции активов в портфеле, начиная от 100% А, далее 90% А:10% В и так далее до 100% В.
Источник: Richard Ferri, Portfolio Solutions
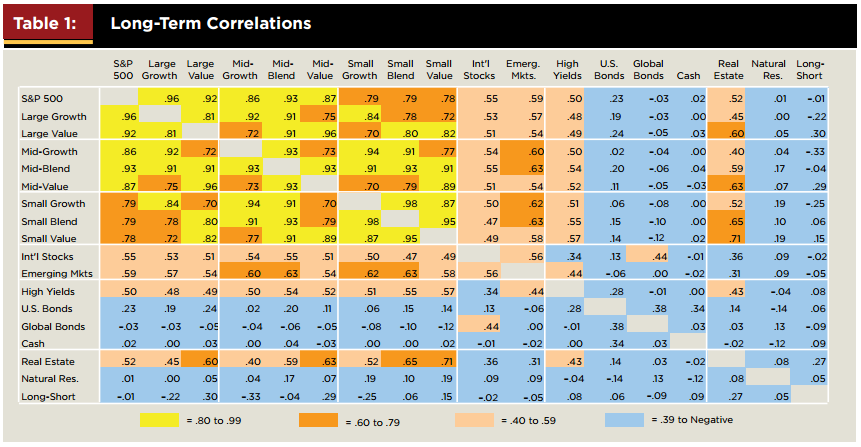
Корреляция активов
К сожалению, в реальной жизни довольно трудно найти два актива с абсолютно нулевой или отрицательной корреляцией. Большинство активов имеют корреляцию где-то между 0 и+1. В таблице 1 представлена матрица корреляции между разными классами активов с 1970 по 2004 год. Чем холоднее цвет, тем ниже корреляция. Можно заметить, что холодные цвета присутствуют в основном у облигаций, кэша и ресурсов. Эти классы активов хуже всего коррелируют с акциями различной капитализации и недвижимостью. Однако даже среди них редко встречаются отрицательные значения.
Источник: Journal of financial planning
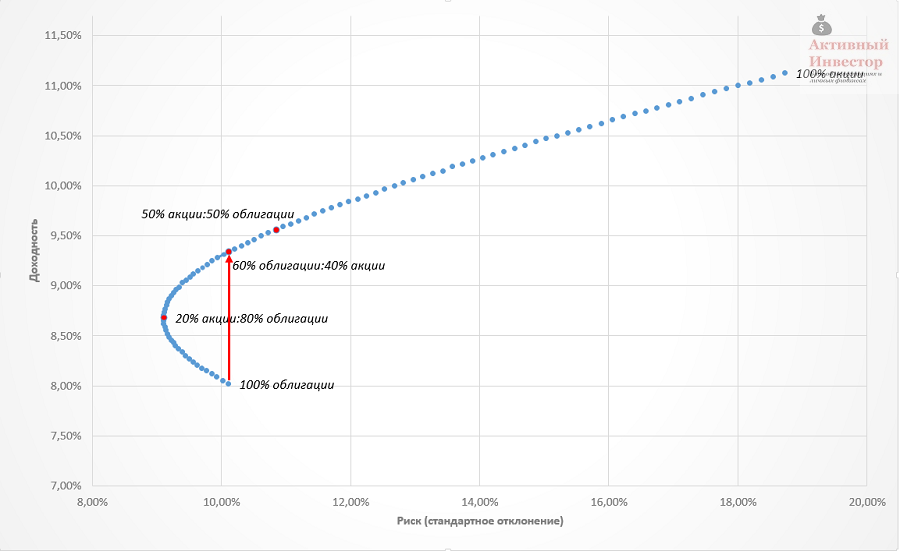
Если взять реальный пример, то корреляция между американскими акциями и долгосрочными государственными облигациями на сроке 1972-2015 составила 0,01, то есть фактически отсутствовала. Граница эффективности портфеля, состоящего их этих двух классов активов очень похожа на линию на графике выше, которая соответствует портфелю из некоррелируемых активов.
Низкая корреляция между активами создает портфельный эффект — когда по характеристикам риск и доходность портфеля может быть лучше активов, из которых он состоит. Логично было бы ожидать, что самый низкий риск будет иметь портфель, состоящий полностью из облигаций. Но в реальности самым низким риском обладает портфель, доля облигаций в котором 80%, а на акции приходится 20%. Добавление акций не только уменьшило риск портфеля, но и увеличило его доходность на 0,6%. Другой портфель 60:40 показал такой же риск, как и 100% облигаций, но его доходность при этом была почти на 1,5% больше.
Корреляция непостоянна
Ричард Ферри в своей статье в журнале Forbes обратил внимание, что, к сожалению, теория, которая красиво выглядит на длительном сроке, не всегда хорошо работает на коротких периодах. Например, с 1926 по 2013 год корреляция между акциями США и 5-летними казначейскими облигациями была равна 0,07. Это очень низкая корреляция для двух классов активов, значит эти два класса активов в портфеле должны хорошо работать вместе.
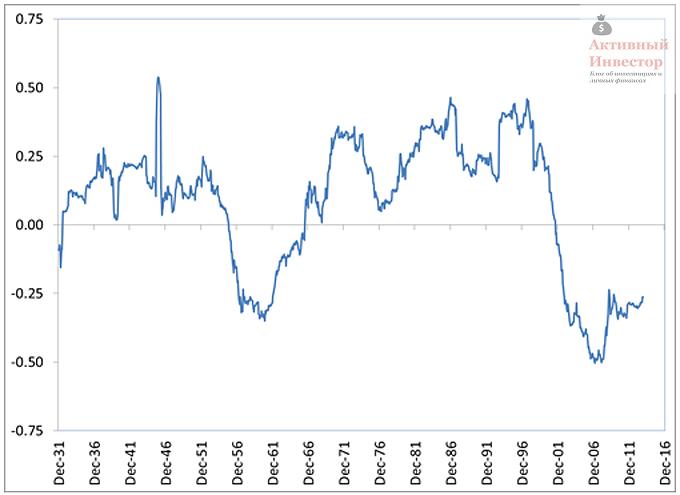
К сожалению, долговременная корреляция не отражает то, что происходит в течение коротких периодов. На графике ниже показано, как сильно может меняться корреляция на коротком сроке. На рисунке изображена 5-ти летняя скользящая корреляция между американскими акциями и 5-летними облигациями, рассчитанная на отрезке 1926-2013.
Источник: Richard Ferri, Portfolio Solutions
Источник: Richard Ferri, Portfolio Solutions
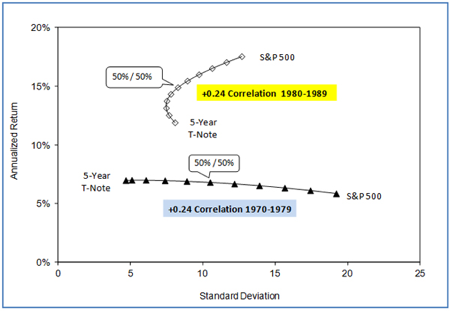
Но даже если корреляция в будущем будет такой же, как она была в прошлом, результаты все равно могут отличаться. Например, 10-летняя корреляция между 5-летними облигациями и акциями США в 70-х годах была +0,24, такой же она была и в 80-х. Но результаты портфелей были различными.
Источник: Richard Ferri, Portfolio Solutions
Низкая корреляция в 70-х годах не дала особых преимуществ: риск портфеля 50/50 оказался выше, а доходность ниже, чем у облигаций. В 80-х аналогичный портфель показал результат гораздо лучше: на 3% больше доходности облигаций при аналогичном риске. Поэтому низкая корреляция двух активов еще не гарантирует уменьшение риска портфеля на коротком сроке.
С течением времени активы с низкой корреляцией находить стало труднее. Финансовые рынки стали более глобальными и взаимосвязанными. Локальный ипотечный кризис 2008 года в США затронул весь мир. Глобализация финансовых рынков сделала так, что инструменты сейчас коррелируют в большей степени, чем раньше. Величина корреляции активов в прошлом зависит от взятого периода и не является надежным индикатором корреляции в будущем.
Тем не менее это вовсе не означает, что про корреляцию можно совсем забыть. В портфель нужно включать фундаментально разные активы. Высокая положительная корреляция означает отсутствие фундаментальных отличий по риску между активами. Например, высокая положительная корреляция между акциями крупной и средней капитализации будет всегда. Диверсификация по таким активам не принесет большой выгоды портфелю в плане снижения риска. Слабая положительная или отрицательная корреляция служит признаком отличий между активами в плане риска, поэтому включение в портфель активов с низкой положительной или отрицательной корреляцией потенциально уменьшает его риск и создает портфельный эффект, о котором будет написана следующая статья.
Что означают положительный, отрицательный и нулевой коэффициенты корреляции?
Опубликовано 29.06.2021 · Обновлено 03.10.2021
Коэффициенты корреляции – это индикаторы силы линейной связи между двумя разными переменными x и y. Коэффициент линейной корреляции больше нуля указывает на положительную взаимосвязь. Значение меньше нуля означает отрицательную связь. Наконец, нулевое значение указывает на отсутствие связи между двумя переменными x и y. В этой статье объясняется значение коэффициента линейной корреляции для инвесторов, как рассчитать ковариацию для акций и как инвесторы могут использовать корреляцию для прогнозирования рынка.
Ключевые выводы:
Понимание корреляции
Коэффициент корреляции ( ρ ) – это мера, которая определяет степень, в которой связано движение двух разных переменных. Наиболее распространенный коэффициент корреляции, генерируемый корреляцией произведения-момента Пирсона, используется для измерения линейной связи между двумя переменными. Однако в нелинейной зависимости этот коэффициент корреляции не всегда может быть подходящей мерой зависимости.
Краткий обзор
При интерпретации корреляции важно помнить, что наличие корреляции между двумя переменными не означает, что одна вызывает другую.
Корреляция и финансовые рынки
На финансовых рынках коэффициент корреляции используется для измерения акции движутся в противоположных направлениях, коэффициент корреляции отрицательный.
Например, предположим, что цены на кофе и компьютеры наблюдаются и обнаруживают корреляцию +,0008. Это означает, что между двумя переменными нет корреляции или взаимосвязи.
Расчет ρ
Стандартное отклонение – это мера разброса данных от среднего значения. Ковариация – это мера того, как две переменные изменяются вместе. Однако его масштабы безграничны, поэтому его трудно интерпретировать. Нормализованная версия статистики вычисляется путем деления ковариации на произведение двух стандартных отклонений. Это коэффициент корреляции.
Положительное соотношение
Положительная корреляция – когда коэффициент корреляции больше 0 – означает, что обе переменные движутся в одном направлении. Когда ρ равно +1, это означает, что две сравниваемые переменные имеют идеальную положительную взаимосвязь; когда одна переменная движется выше или ниже, другая переменная движется в том же направлении с той же величиной.
Чем ближе значение ρ к +1, тем сильнее линейная зависимость. Например, предположим, что стоимость цен на нефть напрямую связана с ценами на авиабилеты с коэффициентом корреляции +0,95. Взаимосвязь между ценами на нефть и стоимостью авиабилетов имеет очень сильную положительную корреляцию, так как значение близко к +1. Таким образом, если цена на нефть снижается, цены на авиабилеты также уменьшаются, а если цена на нефть растет, то же самое происходит и с ценами на авиабилеты.
На приведенной ниже диаграмме мы сравниваем один из крупнейших банков США, JPMorgan Chase & Co. ( биржевым фондом Financial Select SPDR Exchange Traded Fund (ETF) (XLF ).1 Как вы понимаете, компания JPMorgan Chase & Co. должна иметь положительную корреляцию с банковской отраслью в целом. Мы видим, что коэффициент корреляции в настоящее время составляет 0,98, что свидетельствует о сильной положительной корреляции. Значение выше 0,50 обычно свидетельствует о положительной корреляции.
Понимание корреляции между двумя акциями (или одной акцией) и отраслью может помочь инвесторам оценить, как акции торгуются по сравнению с аналогами. Все типы ценных бумаг, включая облигации, сектора и ETF, можно сравнить с помощью коэффициента корреляции.
Отрицательная корреляция
Примеры отрицательной корреляции
Когда дело доходит до инвестирования, отрицательная корреляция не обязательно означает, что следует избегать ценных бумаг. Коэффициент корреляции может помочь инвесторам диверсифицировать свой портфель, включив в него набор инвестиций, имеющих отрицательную или низкую корреляцию с фондовым рынком. Короче говоря, при снижении риска волатильности в портфеле иногда все же привлекаются противоположности.
Коэффициент линейной корреляции
Даже для небольших наборов данных вычисления коэффициента линейной корреляции могут оказаться слишком длинными, чтобы их можно было выполнять вручную. Таким образом, данные часто загружаются в калькулятор или, что более вероятно, в компьютер или статистическую программу, чтобы найти коэффициент.
Коэффициент Пирсона
Простая линейная регрессия описывает линейную связь между переменной ответа (обозначенной y) и независимой переменной (обозначенной x) с использованием статистической модели. Статистические модели используются для прогнозов.
Краткий обзор
Упростите линейную регрессию, вычислив корреляцию с помощью такого программного обеспечения, как Excel.
В финансах, например, корреляция используется в нескольких анализах, включая расчет стандартного отклонения портфеля. Поскольку это требует много времени, корреляцию лучше всего рассчитать с помощью такого программного обеспечения, как Excel. Корреляция объединяет статистические концепции, а именно дисперсию и стандартное отклонение. Дисперсия – это дисперсия переменной вокруг среднего значения, а стандартное отклонение – это квадратный корень из дисперсии.
Поиск корреляции с помощью Excel
В Excel есть несколько методов расчета корреляции. Самый простой – получить два набора данных рядом и использовать встроенную формулу корреляции:
Если вы хотите создать корреляционную матрицу для ряда наборов данных, в Excel есть подключаемый модуль анализа данных, который находится на вкладке «Данные» в разделе «Анализ».
Выберите таблицу доходов. В этом случае наши столбцы имеют заголовки, поэтому мы хотим установить флажок «Ярлыки в первой строке», чтобы Excel обрабатывал их как заголовки. Затем вы можете выбрать вывод на том же листе или на новом листе.
Как только вы нажмете Enter, данные будут созданы автоматически. Вы можете добавить текст и условное форматирование, чтобы очистить результат.
Часто задаваемые вопросы о коэффициенте линейной корреляции
Что такое коэффициент линейной корреляции?
Коэффициент линейной корреляции – это число, вычисленное на основе заданных данных, которое измеряет силу линейной связи между двумя переменными, x и y.
Как найти коэффициент линейной корреляции?
Корреляция объединяет несколько важных и связанных статистических концепций, а именно дисперсию и стандартное отклонение. Дисперсия – это дисперсия переменной вокруг среднего значения, а стандартное отклонение – это квадратный корень из дисперсии.
Вычисления слишком длинные, чтобы их можно было выполнять вручную, и программное обеспечение, такое как Excel или статистическая программа, является инструментами, используемыми для вычисления коэффициента.
Что подразумевается под линейной корреляцией?
Как найти коэффициент линейной корреляции на калькуляторе?
Графический калькулятор необходим для расчета коэффициента корреляции.Следующие инструкции предоставлены Statology.
Шаг 1. Включите диагностику
Вам нужно будет сделать этот шаг на калькуляторе только один раз. После этого вы всегда можете начать с шага 2 ниже. Если вы этого не сделаете, r (коэффициент корреляции) не будет отображаться при запуске функции линейной регрессии.
Нажмите [2nd], а затем [0], чтобы войти в каталог вашего калькулятора. Прокрутите, пока не увидите «DiagnosticsOn».
Нажимайте Enter, пока на экране калькулятора не появится надпись «Готово».
Это важно повторить: вам никогда не придется делать это снова, если вы не перезагрузите калькулятор.
Шаг 2: введите данные
Введите свои данные в калькулятор, нажав [STAT], а затем выбрав 1: Edit. Чтобы упростить задачу, вы должны ввести все свои «данные x» в L1 и все «данные y» в L2.
После того, как вы введете свои данные, вы перейдете к [STAT], а затем к меню CALC вверху. Наконец, выберите 4: LinReg и нажмите Enter.
Это оно! Готово! Теперь вы можете просто считать коэффициент корреляции прямо с экрана (его r). Помните, что если r не отображается на вашем калькуляторе, необходимо включить диагностику. Это то же самое место на калькуляторе, где вы найдете уравнение линейной регрессии и коэффициент детерминации.
Коэффициент линейной корреляции может быть полезен при определении взаимосвязи между инвестициями и рынком в целом или другими ценными бумагами. Его часто используют для прогнозирования доходности фондового рынка. Это статистическое измерение полезно во многих отношениях, особенно в финансовой отрасли. Например, это может быть полезно для определения того, насколько хорошо взаимный фонд ведет себя по сравнению с его эталонным индексом, или его можно использовать для определения того, как взаимный фонд ведет себя по отношению к другому фонду или классу активов. Добавляя взаимный фонд с низкой или отрицательной корреляцией к существующему портфелю, можно получить преимущества диверсификации.