Чем вызвано броуновское движение частиц пыльцы в воде
Броуновское движение
БРОУНОВСКОЕ ДВИЖЕНИЕ (брауновское движение), беспорядочное движение мельчайших частиц, взвешенных в жидкости или газе, происходящее под действием ударов молекул окружающей среды; открыто Р. Броуном в 1827 г.
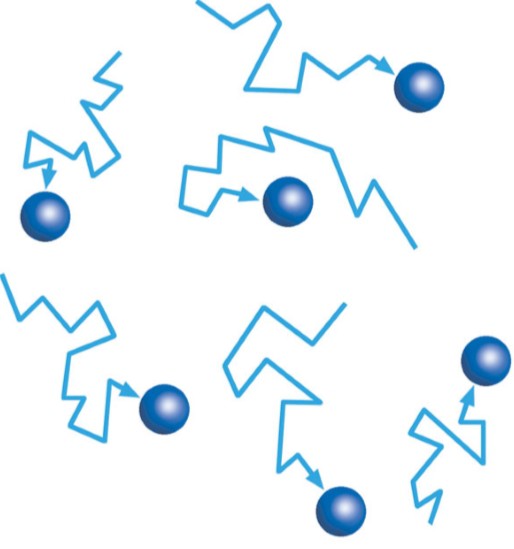
При наблюдении в микроскопе взвеси цветочной пыльцы в воде Броун наблюдал хаотичное движение частиц, возникающее «не от движения жидкости и не от ее испарения». Видимые только под микроскопом взвешенные частицы размером 1 мкм и менее совершали неупорядоченные независимые движения, описывая сложные зигзагообразные траектории. Броуновское движение не ослабевает со временем и не зависит от химических свойств среды, его интенсивность увеличивается с ростом температуры среды и с уменьшением ее вязкости и размеров частиц. Даже качественно объяснить причины броуновского движения удалось только через 50 лет, когда причину броуновского движения стали связывать с ударами молекул жидкости о поверхность взвешенной в ней частицы.
Первая количественная теория броуновского движения была дана А. Эйнштейном и М. Смолуховским в 1905-06 гг. на основе молекулярно-кинетической теории. Было показано, что случайные блуждания броуновских частиц связаны с их участием в тепловом движении наравне с молекулами той среды, в которой они взвешены. Частицы обладают в среднем такой же кинетической энергией, но из-за большей массы имеют меньшую скорость. Теория броуновского движения объясняет случайные движения частицы действием случайных сил со стороны молекул и сил трения. Согласно этой теории, молекулы жидкости или газа находятся в постоянном тепловом движении, причем импульсы различных молекул не одинаковы по величине и направлению. Если поверхность частицы, помещенной в такую среду, мала, как это имеет место для броуновской частицы, то удары, испытываемые частицей со стороны окружающих ее молекул, не будут точно компенсироваться. Поэтому в результате «бомбардировки» молекулами броуновская частица приходит в беспорядочное движение, меняя величину и направление своей скорости примерно 1014 раз в сек. Из этой теории следовало, что, измерив смещение частицы за определенное время и зная ее радиус и вязкость жидкости можно вычислить число Авогадро.
Выводы теории броуновского движения были подтверждены измерениями Ж. Перрена и Т. Сведберга в 1906 г. На основе этих соотношений были экспериментально определены постоянная Больцмана и постоянная Авогадро.
При наблюдении броуновского движения фиксируется положение частицы через равные промежутки времени. Чем короче промежутки времени, тем более изломанной будет выглядеть траектория движения частицы.
Закономерности броуновского движения служат наглядным подтверждением фундаментальных положений молекулярно-кинетической теории. Было окончательно установлено, что тепловая форма движения материи обусловлена хаотическим движением атомов или молекул, из которых состоят макроскопические тела.
Теория броуновского движения сыграла важную роль в обосновании статистической механики, на ней основана кинетическая теория коагуляции водных растворов. Помимо этого, она имеет и практическое значение в метрологии, так как броуновское движение рассматривают как основной фактор, ограничивающий точность измерительных приборов. Например, предел точности показаний зеркального гальванометра определяется дрожанием зеркальца, подобно броуновской частице бомбардируемого молекулами воздуха. Законами броуновского движения определяется случайное движение электронов, вызывающее шумы в электрических цепях. Диэлектрические потери в диэлектриках объясняются случайными движениями молекул-диполей, составляющих диэлектрик. Случайные движения ионов в растворах электролитов увеличивают их электрическое сопротивление.
Другие статьи в литературном дневнике:
Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и российского законодательства. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.
© Все права принадлежат авторам, 2000-2021 Портал работает под эгидой Российского союза писателей 18+
Броуновское движение
Броуновское движение — это беспорядочные перемещения малых частиц, возникающие вследствие их столкновения с невидимыми молекулами воды или газа. Первым его обнаружил ботаник Роберт Броун — частицы пыльцы, которые он разглядывал под микроскопом на мокром предметном стекле, двигались рывками, — однако описать математически смог только Альберт Эйнштейн. Броуновское движение объясняет, как распространяется в спокойном воздухе пыльца, но и описывает также множество случайных процессов — от наводнений до скачков на фондовом рынке. Его непредсказуемые рывки связаны с фракталами.
В XIX веке ботаник Роберт Броун, разглядывая под микроскопом частицы пыльцы, обнаружил, что они не стоят на месте, но отрывисто двигаются. На миг он задумался — уж не живые ли они? Нет, конечно, просто их сбивали с места молекулы воды, которой Броун смачивал предметные стекла. Частицы пыльцы двигались хаотично, иногда лишь немного, иногда на довольно большие расстояния, и, в конечном счете, совершали по стеклу путь, предсказать который было невозможно. И многие ученые начали задумываться над открытием Броуна, названным в его честь «броуновским движением».
Случайное блуждание
Броуновское движение совершается любыми малыми частицами, находящимися во взвешенном состоянии в жидкости или газе. Его можно наблюдать даже у довольно больших частиц, например частиц дыма, — при большом увеличении видно, какие зигзаги они описывают в воздухе. Сила получаемых частицами ударов зависит от импульса молекул. Она оказывается большей в случае тяжелых молекул жидкости либо газа — как и в случае быстро движущихся, например, молекул нагретой жидкости.
Во второй половине XIX века предпринималась не одна попытка описать броуновское движение математически, однако сделать это смог лишь Эйнштейн в 1905 году, когда он также опубликовал специальную теорию относительности и дал описание фотоэффекта, за что получил Нобелевскую премию. Эйнштейн воспользовался тепловой теорией, основанной на столкновениях молекул, и успешно объяснил движения частиц, которые наблюдал Броун. Поняв, что броуновское движение доказывает существование молекул жидкостей, физики вынуждены были принять и учение об атомах, которое даже в начале XX века еще вызывало сомнения.
Диффузия
Со временем броуновское движение способно заставить частицу пройти значительное расстояние, хоть, разумеется, и не такое, какое она могла бы пройти, если бы никто не мешал ей двигаться по прямой. Это объясняется случайным характером движения молекул, которые с равной вероятностью могут толкать ее и вперед, и назад. Поэтому, если уронить в жидкость плотную группу частиц, они начнут рассеиваться (диффундировать) во все стороны даже при том, что жидкость никто не будет помешивать и никакие потоки в ней не возникнут. Каждая частица пойдет по своему пути, и капля начнет расширяться, образуя диффузное облако. Такое рассеяние играет важную роль в распространении загрязнений воздуха, имеющих точечный источник, например в распространении аэрозоля в атмосфере. Даже при полном отсутствии ветра химические вещества будут рассеиваться в воздухе вследствие одного лишь броуновского движения.
Фракталы
Путь, по которому следует частица, совершающая броуновское движение, дает нам пример фрактала. Каждый прямой отрезок этого пути может иметь любую длину и любое направление, однако некоторый общий рисунок все же существует. Этот рисунок несет в себе определенную структуру, в каком масштабе его ни разглядывай — от наименьшего из вообразимых до очень больших. А это и есть определяющее свойство фрактала.
Фракталы были в 1960-х и 1970-х предложены Бенуа Мандельбротом как метод представления самоподобных фигур в количественной форме. Фракталы — это фигуры, которые при любом масштабе выглядят одинаково. Если увеличить малый кусочек этой фигуры, вы увидите точно такую же, неотличимую от первой, рассматриваемой в большем масштабе, поэтому определить степень увеличения, глядя на фигуру, ни за что не удастся. Такая безмасштабная повторяемость часто встречается в природе — в рисунке береговой линии, в ветвях дерева, в листьях папоротника, в шестикратной симметрии снежинки.
Фракталы отличаются тем, что их длина или размерность не зависят от того, с каким увеличением вы их рассматриваете. Если вы решите измерить расстояние между двумя приморскими городами, Лендс-Эндом и Маунтс-Беем, то, скорее всего, придете к выводу, что оно составляет 30 км, однако вспомните про все береговые скалы и попробуйте обвить каждую веревкой — и вы обнаружите, что веревка вам понадобится в сотню километров длиной. Если же вы пойдете еще дальше и затеете обмерять каждую песчинку берега, веревку придется удлинить до многих сотен километров. Выходит, что абсолютная длина береговой линии зависит от масштаба, в котором вы проводите измерения. Ограничьтесь грубым очертанием берега — и вы снова вернетесь к уже знакомым вам 30 км. В этом смысле фрактальная размерность есть мера огрубления чего-то, будь то облако, дерево или горный хребет. Многие из фрактальных форм, например береговую линию, можно получить соединением шагов случайного движения — отсюда и их связь с броуновским движением.
Математика броуновского движения, или последовательность случайных шагов, может использоваться для создания фрактальных фигур, находящих применение во многих областях науки. С ее помощью можно создавать грубо очерченные виртуальные пейзажи — горы, деревья, облака — компьютерных игр, ее можно использовать в программах пространственного картирования, которые помогают роботам двигаться по сильно пересеченной местности, моделируя ее возвышенности и низины. Врачи применяют ее для медицинской визуализации, когда у них возникает нужда проанализировать структуру сложных органов тела, скажем легких, в которых ветвящиеся структуры присутствуют во всех масштабах, от грубого до совсем малого.
Идеи броуновского движения используются и для предсказания рисков либо событий будущего, которые являются суммарным результатом множества случайных воздействий — наводнений, колебаний фондового рынка. Фондовый рынок можно рассматривать как портфель ценных бумаг, стоимость которых варьируется случайным образом, напоминая броуновское движение множества молекул. Фигурирует оно и в моделировании других социальных процессов, относящихся к производству товаров и принятию решений. Броуновское движение с его случайным характером обладает значительным влиянием и появляется во множестве обличий — не в одном только танце чаинок в чашке горячего чая.
Броуновское движение
7 класс, без форм заявки
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Молекулярно-кинетическая теория
Мы состоим из клеток, клетки состоят из молекул, молекулы из атомов, атомы из… Ладно, пока достаточно атомов. И молекулы, и атомы подчиняются законам, которые описаны в молекулярно-кинетической теории.
В основе молекулярно-кинетической теории лежат три основных положения:
Броуновское движение
Во второй половине ХIХ века в научных кругах разгорелась нешуточная дискуссия о природе атомов. На одной стороне дискуссии утверждали, что атомы — просто математические функции, удачно описывающие физические явления и не имеющие под собой реальной физической основы.С другой стороны настаивали, что атомы — это реально существующие физические объекты.
Самое смешное в этих спорах то, что за десять лет до их начала ботаник Роберт Броун уже провел эксперимент, который доказал физическое существование атомов. Вот, как это было:
Как Броун проводил эксперимент
Броун изучал поведение цветочной пыльцы под микроскопом и обнаружил, что отдельные споры совершают абсолютно хаотичные движения.
Представьте себе, что мы издалека наблюдаем, как плотная толпа людей толкает над собой большой мяч. Причём каждый толкает мяч, куда хочет. Мы не видим отдельных игроков, потому что поле далеко от нас, но мяч мы видим — и замечаем, что перемещается он очень беспорядочно.
Мяч постоянно меняет направление своего движения, и пойти в какую-нибудь определенную сторону не желает. Предсказать его местоположение через заданное время — нельзя.
Вот что-то похожее на это Броун увидел при изучении пыльцы.
В первую очередь он начал грешить на движение потоков воды или ее испарение, но проверив эту гипотезу, отмел ее. Проведя множество экспериментов, Броун установил, что такое хаотичное движение свойственно любым микроскопическим частицам — будь то пыльца растений, взвеси минералов или вообще любая измельченная субстанция. Но причины этого явления он выяснить не смог (не в обиду ботаникам, но все же, это не его специализация).
А теперь угадайте, кто смог применить этот эксперимент в доказательстве атомной теории строения вещества. Альберт Эйнштейн, кто же еще. Он объяснил его примерно так: взвешенная в воде спора подвергается постоянной «бомбардировке» со стороны хаотично движущихся молекул воды.
В среднем, молекулы воздействуют на нее со всех сторон с равной интенсивностью и через равные промежутки времени. Однако, как бы ни мала была частица, в силу чисто случайных отклонений сначала она получает импульс со стороны молекулы, ударившей ее с одной стороны, а затем — со стороны молекулы, ударившей ее с другой. И так далее.
Чуть позже, через 3 года после открытия Эйнштейна, в 1908 году французский физик Жан Батист Перрен провел серию опытов, которые подтвердили правильность эйнштейновского объяснения броуновского движения. Стало окончательно ясно, что наблюдаемое «хаотичное» движение броуновских частиц происходит вследствие межмолекулярных соударений. Поскольку вывод о том, что несуществующие в природе математические функции не могут привести к физическому взаимодействию, напрашивается сам собой, стало окончательно ясно, что спор о реальности атомов окончен: они существуют в природе.
Также, если еще раз посмотреть на второе положение молекулярно-кинетической теории, можно заметить, что броуновское движение очень хорошо его доказывает: Атомы и молекулы находятся в непрерывном хаотическом движении.
Диффузия
Явление, которое доказывает первое и второе положения молекулярно-кинетической теории называется диффузия.
Диффузия в газах
Если в комнате открыть флакон с духами или зажечь ароматизированную свечу, то запах вскоре будет чувствоваться во всей комнате. Распространение запахов происходит из-за того, что молекулы духов проникают между молекулами воздуха. На самом деле, в этом процессе очень большую роль играет такой вид теплопередачи, как конвекция, но и без диффузии не обошлось.
На самом деле, молекулы вокруг нас движутся очень быстро — со скоростью в сотни метров в секунду — это напрямую зависит от температуры.
Давайте проверим это сами несложным экспериментом:
Замерьте температуру воздуха в помещении. Распылите освежитель воздуха в одном углу, встаньте в другой и включите секундомер. А лучше проведите эксперимент вдвоем, чтобы один человек распылял, а другой включал секундомер — так не будет погрешности, но будет веселье 😉
Как только почувствуете аромат освежителя в противоположном от места распыления, выключите секундомер. Запишите результат измерения. А потом проветрите помещение и проделайте все то же самое. Время, через которое до вас дойдет запах, будет другим. Во втором случае аромат будет распространяться медленнее.
То есть, чем выше температура, тем больше скорость диффузии.
Диффузия в жидкостях
Если диффузия в газах происходит быстро — чаще всего за считанные секунды — то диффузия в жидкостях занимает минуты или в некоторых случаях часы. Зачастую это зависит от температуры (как и в эксперименте выше) и плотности вещества.
С диффузией в жидкостях вы встречаетесь, когда, например, размешиваете краску. Или когда смешиваете любые две жидкости, например, газировку с сиропом. Также из-за диффузии происходит загрязнение рек (да и в целом окружающей среды).
Ну или вот пример диффузии в жидкостях, с которым вы точно не встречались — акулы ищут свою жертву по запаху крови, который распространяется в океане за счет диффузии.
Диффузия в твёрдых телах
Диффузия в твёрдых телах происходит очень медленно. Например, при комнатной температуре (около 20 °С) за 4-5 лет золото и свинец взаимно проникают друг в друга на расстояние около 1 мм.
Кстати, если вы проведете такой эксперимент, то увидите, что в свинец проникло малое количество золота, а свинец проник в золото на глубину не более одного миллиметра. Такое различие обусловлено тем, что плотность свинца намного выше плотности золота.
Этот процесс можно ускорить за счет нагревания, как в жидкостях и газах. Если на тонкий свинцовый цилиндр нанести очень тонкий слой золота, и поместить эту конструкцию в печь на неделю при температуре воздуха в печи 200 градусов Цельсия, то после разрезания цилиндра на тонкие диски, очень хорошо видно, что свинец проник в золото и наоборот.
Чем вызвано броуновское движение частиц пыльцы в воде
Роберт Броун (1773-1858)
Шотландский ботаник. Родился в Монтроузе в семье священника. Получил медицинское образование в Эдинбургском университете, работал военно-полевым хирургом. В 1798 г., познакомившись с Джозефом Бэнксом (1743-1820), выдающимся ботаником своего времени, настолько заинтересовался этой наукой, что решил в корне изменить свою карьеру и достиг в ботанике высот, которым его учитель позавидовал бы. В качестве натуралиста Броун плавал к берегам Австралии. Со временем занял пост главы ботанического отдела Британского музея. Открыл, идентифицировал, классифицировал и изучил морфологию множества растений. Однако прославился, прежде всего, благодаря открытию им броуновского движения.
Молекулы в любом теле находятся в состоянии непрерывного хаотического движения.
Впервые и наиболее убедительно движение молекул обнаружил Броун в 1826 г.
 Рис. 1.1 |
Наблюдая в микроскоп цветочную пыльцу, взвешенную в воде, он увидел, что каждая частица пыльцы совершает быстрые беспорядочные движения, перемещаясь на небольшое расстояние. В результате отдельных перемещений каждая частица пыльцы двигалась по зигзагообразной траектории. Это движение небольших частиц и было названо броуновским (рис. 1.1).
Дальнейшие исследования этого явления в различных жидкостях и с различными твердыми частицами показали, что это движение становится тем интенсивнее, чем меньше размеры частиц и чем выше температура опыта.
Это движение никогда не прекращается и не зависит ни от каких внешних причин.
 Рис. 1.2 |
Движущиеся молекулы жидкости при столкновении с взвешенными в ней частицами передают им некоторый импульс (рис. 1.2). Если частица велика, то число молекул, налетающих на нее со всех сторон, также очень велико, их удары в каждый данный момент компенсируются, и частица остается практически неподвижной. Однако если частица очень мала, то может случиться, что с одной стороны об нее ударится большее количество молекул, чем с другой, в результате частица придет в движение. Именно такое движение под влиянием беспорядочных ударов молекул и совершают броуновские частицы. И хотя броуновские частицы в миллиарды раз больше по массе, чем отдельные молекулы, и скорости их весьма малы, по сравнению со скоростями молекул, но все же их движение таково, что может быть замечено в микроскоп.
Чем вызвано броуновское движение частиц пыльцы в воде
A93340 Броуновское движение частиц пыльцы в воде вызвано
Отзыв
непрерывностью и хаотичностью теплового движения молекул воды
Вопрос 5
Текст вопроса
92C57F Дым представляет собой частицы сажи, взвешенные в воздухе. Твердые частицы сажи долго не падают вниз потому, что
Отзыв
частицы сажи совершают броуновское движение в воздухе
Вопрос 6
Текст вопроса
Броуновское движение частиц пыльцы в воде объясняется
Отзыв
непрерывностью и хаотичностью теплового движения молекул воды
Вопрос 7
Текст вопроса
Броуновское движение частиц пыльцы в воде объясняется
Отзыв
непрерывностью и хаотичностью теплового движения молекул воды
Вопрос 8
Текст вопроса
Броуновским движением является
Отзыв
беспорядочное движение мелких пылинок в воздухе
Вопрос 9
Текст вопроса
Отзыв
равнодействующей сил действия молекул жидкости на частицу
Вопрос 10
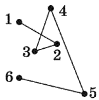
Текст вопроса
Отзыв
двигалась так, что закономерностей в форме ее траектории обнаружить не удалось
Вопрос 11
Текст вопроса
3D641E Явление диффузии в жидкостях объясняется тем, что молекулы жидкостей
Отзыв
могут хаотично перемещаться по объёму
Вопрос 12
Текст вопроса
EF6C1E Укажите пару веществ, скорость диффузии которых наименьшая при прочих равных условиях:
Отзыв
свинцовая и медная пластины
Вопрос 13
Текст вопроса
576896 Явление диффузии в жидкостях свидетельствует о том, что молекулы жидкостей
Отзыв
Вопрос 14
Текст вопроса
44FF66 В каких телах – твёрдых, жидких или газообразных – происходит диффузия?
Отзыв
в твёрдых, жидких и газообразных
Вопрос 15
Текст вопроса
D5D68D Диффузия в жидкости происходит быстрее при повышении температуры, потому что с повышением температуры
Отзыв
увеличивается скорость теплового движения молекул
Вопрос 16
Текст вопроса
6BF6CE Какое из утверждений правильно?
А. Диффузия наблюдается только в газах и жидкостях.
Б. Диффузия наблюдается только в твердых телах.
В. Диффузия наблюдается в газах, жидкостях и твердых телах.
Отзыв
Вопрос 17
Текст вопроса
Как зависит скорость диффузии от агрегатного состояния вещества при постоянной температуре?
Отзыв
Скорость максимальна в газах
Вопрос 18
Текст вопроса
Как зависит скорость диффузии от температуры для данного агрегатного состояния вещества?
Отзыв
Увеличивается с повышением температуры
Вопрос 19
Текст вопроса
Если в стакан с водой бросить несколько кристаллов марганцовки, то в результате растворения марганцовки около дна стакана сначала образуется тонкий темно окрашенный слой раствора, а остальная вода остается светлой. Затем в результате теплового движения молекулы растворенного вещества проникают в промежутки между молекулами жидкости и постепенно вся вода оказывается равномерно окрашенной. Это явление называется