Чем вызваны фазовые искажения в раскрыве рупора

Принцип действия, основные свойства рупорных антенн

Концентрация излучения в пределах более узкого телесного угла достигается увеличением размеров синфазно возбужденной поверх­ности. Если размеры сечения волновода выбираются таким образом, чтобы обеспе­чить формирование необходимой структу­ры поля, то, плавно увеличивая сечение волновода, эту структуру можно сохранить, а размеры излучаемой поверхности увели­чить (рис. 2). В месте перехода от вол­новода к рупору (сечение S’) возникают высшие типы волн, но при достаточно плавном расширении волновода (малый угол раствора рупора) интен­сивность этих волн невелика.

Рис. 2 – Вид рупорной антенны

Векторы электромагнитного поля при переходе из волновода в рупор несколько изменяют свою форму, чтобы обеспечить выполне­ние граничных условий на стенках рупора (рис. 3).

Направленные свойства рупорной антенны приближенно мож­но анализировать, как и в случае открытого конца волновода, пользу­ясь принципом эквивалентности. На излучающей поверхности рупора действуют две взаимно перпендикулярные тангенциальные составляющие поля Е_y H_x (прямоугольный раскрыв), амплитуды которых не зависят от координаты y, а вдоль координаты х они изменяются по закону косинуса.

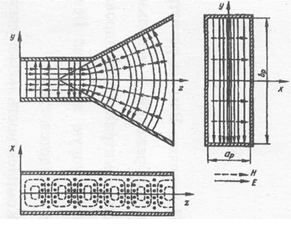Рис. 3 – Изменение векторов электромагнитного поля при переходе из волновода в рупор

Однако в отличие от поверхно­сти открытого конца волновода плос­кая излучающая поверхность рупора не может быть синфазной, так как в раскрыве рупора имеются фазовые искажения. Определение фазы возбуждающего поля в произвольной точке М излучающего раскрыва Н-плоскостного рупора осуществляется на основе рис. 4.

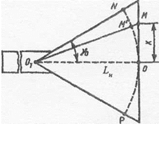Рис. 4 – Графическая интерпретация раскрыва Н-плоскостного рупора

Поскольку в рупорной антенне практически невозможно добить­ся полной синфазности излучающей поверхности, то обычно, задава­ясь некоторым допустимым сдвигом фаз, выбирают размеры раскры­ва рупора и его длину. Этот сдвиг должен быть таким, чтобы ДН ру­порной антенны мало отличалась от ДН синфазной излучающей по­верхности, размеры которой равны размерам раскрыва рупора. В дан­ном случае характеристику направленности рупорной антенны можно рассчитать по формулам, приведенным в справочниках, заменяя в множителях системы L соответствующими размерами рупора, a cos Θ на sinΘ.

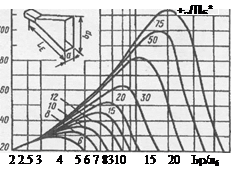Рис. 5 – Зависимость КНД E-плоскостного рупора от отношения λ_b/а_р

Допустимый максимальный сдвиг фаз определяется условием получения максимального КНД при заданной относительной длине L/λ рупора. С увеличением относительных размеров раскрыва рупора (а_р /λ или b_р /λ) при неизменной длине его ДН сначала становится уже и КHД растет, так как увеличиваются размеры излучающей поверхнос­ти, которая практически остается синфазной (сдвиг фаз ψ_max мал). При дальнейшем увеличении размеров заметно растут фазовые искажения, вследствие чего ДН начинает расширяться и КНД уменьшается. На рис. 5 по оси ординат отложено произведение КНД E-плоскостного рупора на отношение λ_b/а_р. Аналогичные кривые существуют и для Н-плоскостных рупоров. При заданном отношении L/λ имеется имеется оптимальное значение а_р/λ или b_p/λ при котором КНД антенны – максимально возможный.

Увеличение допустимого сдвига фаз в случае Н-плоскостного рупора по сравнению с Е-плоскостным объясняется спаданием амп­литуды возбуждающего поля к краям этого рупора в плоскости Н.

В настоящее время находят применение рупоры, у которых сдви­ги фаз поля в раскрыве значительно превосходят максимально допус­тимые. При больших по сравнению с λ раскрывах а_р и b_р и больших углах растворов рупора γ₀ ДН становится по форме близкой к столооб­разной. Такие расфазированные рупоры обладают более широким рабочим диапазоном, чем синфазные рупоры.

7.1.3. Рупорные антенны с круговой поляризацией поля

Для получения круговой (или близкой к ней) поляризации излу­чаемого рупором поля применяются фазирующие секции, устанавли­ваемые в волноводе, питающем рупор. В фазирующей секции проис­ходят разложение вектора линейно поляризованного электромагнит­ного поля на две взаимно перпендикулярные составляющие, лежащие в плоскости, перпендикулярной направлению распространения вол­ны, и обеспечение между ними на выходе секции сдвига фаз в 90°.

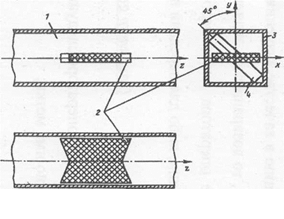Существуют различные фазирующие секции. В качестве фази­рующей секции можно, например, использовать отрезок волновода с квадратным поперечным сечением, возбуждаемый прямоугольным волноводом с волной Н10. Возбуждающий волновод соединяется с фа­зирующей секцией плавным пирамидальным переходом. Поперечные сечения возбуждающего волновода и фазирующей секции повернуты относительно друг друга на 45° (рис. 6).

Рис. 6 – Фазирующие секции

В результате вектор Е поля в фазирующей секции будет иметь составляющие Е_х и Е_у, параллельные взаимно перпендикулярным стенкам. Таким образом, поле в секции можно рассматривать как суперпозицию волн Н₁₀ и Н₀₁.

Для создания необходимого сдвига фаз между составляющими Е_х и Е_у в фазирующую секцию (1) устанавливают тонкую диэлектри­ческую пластинку (2), причем так, чтобы большой размер ее попереч­ного сечения был параллелен либо составляющей Е_х, либо Е_у. Такая пластинка влияет в основном на фазовую скорость той волны, линии вектора Е которой параллельны поверхности пластины. Толщина пла­стинки выбирается достаточно малой по сравнению с рабочей длиной волны. Тем самым она не оказывает заметного влияния на фазовую скорость волны, вектор Е которой перпендикулярен поверхности пла­стины.

При квадратном раскрыве пирамидального рупора ширина глав­ного лепестка ДН в двух взаимно перпендикулярных плоскостях по­лучается неодинаковой из-за различных амплитудных распределений возбуждающего поля в Е- и Н-плоскостях. В Н-плоскости ДН (по ну­лям) примерно в 1,5 раза шире, чем в Е-плоскости. Между тем в ряде случаев желательно иметь одинаковые ДН в обеих плоскостях. Это особенно важно при круговой поляризации излучаемого поля.

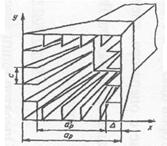
Один из способов получения одинаковых ДН состоит в том, что в квадратном раскрыве устанавливаются металлические ребра высо­той ∆ на расстоянии с

Рис. 7 – Реализация способа получения одинаковых ДН

Источник

Основные теоретические сведения. Направленные свойства рупорных антенн

Направленные свойства рупорных антенн

В диапазоне сантиметровых волн широкое применение находят рупорные антенны. Чаще всего эти антенны используются в качестве облучателей более сложных антенн, таких как параболические, рупорно-линзовые. Рупорные антенны применяются также как элементы антенных решеток. Рупорные антенны конструктивно просты и работают в широком диапазоне частот.

Рупорные антенны представляют собой волновод с плавно увеличивающимися размерами поперечного сечения. В зависимости от формы раскрыва рупоры бывают прямоугольные или конические.

Применяются два типа прямоугольных рупоров: секториальные и пирамидальные (рис.3.1). Секториальными называются рупоры, у которых расширяется только одна пара стенок. В зависимости от того, в какой плоскости происходит расширение, различают Е-секториальные (рис.3.1,а) и Н-секториальные (рис.3,б) рупоры. Если расширение происходит одновременно в плоскости Е и в плоскости Н, то рупор называется пирамидальным (рис.3.1,в).

Рис.3.1.Типы рупорных антенн

Рупоры круглого сечения обычно расширяются равномерно во всех направлениях. Такие рупоры называются коническими (рис. 3.1,г). В данной работе исследуются рупоры с прямоугольным раскрывом.

При анализе направленных свойств рупорных антенн можно считать, что излучение происходит только с поверхности раскрыва рупора (апертуры). В действительности, выходящая из волновода волна дифрагирует на краях раскрыва и наводит токи на наружной поверхности стенок рупора. Однако практически без больших погрешностей излучением за счет этих токов можно пренебречь. Причем, как следует из законов геометрической оптики, погрешность будет тем меньше, чем больше размеры раскрыва по отношению к длине волны.

Поверхность раскрыва рупора можно представить как плоскостную решетку, состоящую из элементов Гюйгенса. В этом случае формулу для диаграммы направленности в плоскостях Е можно записать в следующем виде:

, (3.1)

где F₁(j) –диаграмма направленности элемента Гюйгенса,

F_c(φ) – множитель системы (решетки).

В плоскости Е выражение для F₁(j) имеет вид:

. (3.2)

В плоскости Н диаграмма направленности элемента Гюйгенса аналогична (3.2).

Диаграмма направленности элемента Гюйгенса при практических расчетах обычно не учитывается, как мало влияющая на результирующую ДН рупорной антенны.

Для удобства расчетов раскрыв рупора как излучающую поверхность можно представить в виде непрерывной плоскостной решетки, состоящей из элементов Гюйгенса.

Множитель F_с(j,θ), определяющий направленные свойства этой решетки, зависит от распределения амплитуды и фазы поля в раскрыве рупора. Для достаточно длинного рупора с относительно малыми размерами раскрыва, поле в раскрыве можно в первом приближении считать синфазным.

Распределение амплитуды поля в раскрыве рупора такое же, как в сечении питающего волновода. Для основного типа волны Н₁₀ распределение поля в плоскостях Е и Н показано на рис.3.2.

Как видно на рис. 3.2, в плоскости Е раскрыва рупора распределение амплитуды поля равномерное, и множитель системы без учета фазовых искажений определяется по формуле:

В плоскости Н амплитуда распределяются по закону

, (3.4)

т.е. амплитуда поля в центре раскрыва максимальна, а на краях равна нулю. В соответствии с этим множитель системы для плоскости Н:

. (3.5)

Максимальные значения множителя системы в плоскости Е (3.3) соответствуют значениям аргумента синуса в числителе кратным :

, (3.6)

где m = 0,1,2,3…, а минимальные значения соответствуют значениям аргумента синуса кратные p :

. (3.7)

Соответственно, для плоскости Н максимумы множителя системы (3.5) соответствуют условию :

(3.8)

а минимумы – условию

. (3.9)

Следует отметить, что уменьшение амплитуды поля к краям раскрыва рупора в плоскости Н ведет к расширению основного лепестка диаграммы направленности, что объясняется уменьшением размера эквивалентного раскрыва в этой плоскости. Расширение главного лепестка сопровождается значительным снижением интенсивности бокового излучения. При синусоидальном распределении амплитуды уровень первого бокового лепестка составляет примерно 2%, а при равномерном распределении – 7% от максимального уровня основного лепестка.

Из сказанного следует, что, если рупор имеет квадратный раскрыв (L_Е = L_Н), то в плоскости Е ширина главного лепестка диаграммы направленности будет меньше, чем в плоскости Н, а уровень боковых лепестков в плоскости Е больше, чем в плоскости Н.

Определим условие, при котором ширина основного лепестка в плоскостях Е и Н будет одинаковой. Для этого приравняем аргумент синуса в формуле (3.3) к величине π, а в формуле (3.5) аргумент косинуса к величине равной :

(3.10)

откуда , .

Таким образом, для того, чтобы j_{0 =}θ₀ необходимо, чтобы размер раскрыва в плоскости Н был в 1,5 раза больше, чем в плоскости Е.

Если размеры раскрыва рупора составляют несколько длин волн, то направленными свойствами элемента Гюйгенса можно пренебречь и учитывать только множитель системы.

Расчет диаграммы направленности следует начинать с определения углов j и θ, соответствующих максимальным и минимальным (нулевым) значениям множителей F_c (j) или F_с (θ). Затем в пределах основного лепестка и первого бокового лепестка выбирают дополнительно 4-5 значений углов j или θ.

По выбранным значениям j и θ рассчитываются диаграммы направленности F(j) или F(θ).

Удобнее и проще диаграмму направленности рассчитывать, воспользовавшись ЭВМ. В этом случае шаг углов можно выбрать сколь угодно малым.

При рассмотрении влияния амплитудного распределения поля в раскрыве антенны на ее направленные свойства мы полагали, что поверхность раскрыва рупора возбуждена синфазно. Однако, поле в раскрыве рупора в принципе не синфазно. В рамках лучевой трактовки, это можно объяснить тем, что центральный и периферийные лучи проходят разные пути от горловины до раскрыва рупора (рис.3.3).

За счет этого фаза поля на краях рупора будут отличатся от фазы в центре. Возникают, так называемые «фазовые искажения» («фазовые ошибки»).

Рис.3.3. К вопросу о причинах фазовых искажений в раскрыве рупора

Чем больше угол раскрыва рупора, тем больше разность хода между центральным лучом и лучом периферийным, приходящим к краю раскрыва, и тем больше фазовые искажения Dj = kDr на его краях. Фазовые искажения в раскрыве рупора приблизительно подчинены квадратичному закону. Нарушение синфазности излучающей поверхности приводит к искажениям диаграммы направленности антенны. Искажения, вызванные квадратичным фазовым распределением, сводятся к расширению главного лепестка диаграммы направленности, увеличению интенсивности боковых лепестков и к исчезновению нулевых провалов между лепестками. Причем степень искажений диаграммы направленности зависит также от амплитудного распределения поля в раскрыве антенны.

При равномерном амплитудном распределении (плоскость Е) диаграмма направленности исказится больше, чем при косинусоидальном (плоскость Н). Поэтому в рупорной антенне для плоскости Е допускаются меньшие фазовые искажения, чем в плоскости Н.

Коэффициент направленного действия (КНД) рупорной антенны зависит от его размеров. С увеличением угла раскрыва увеличивается площадь раскрыва и соответственно увеличивается КНД. Однако при этом увеличивается фазовые искажения поля в раскрыве, из-за чего КНД уменьшается. Поэтому максимальному КНД соответствует определенное соотношение угла раскрыва рупора и его площади. Если зафиксировать длину рупора и увеличивать угол раскрыва, то при определенном угле γ_опт КНД становится максимальным. Такой рупор называется оптимальным. При этом в плоскости Е длина оптимального рупора может быть определена из соотношения:

, (3.11)

а в плоскости Н из соотношения:

. (3.12)

В случае оптимального рупора фазовые искажения на его краях в плоскости Е: , а в плоскости Н: .

Согласование рупорных антенн с питающим волноводом

Основная часть электромагнитной энергии излучается рупором в окружающее пространство. При этом некоторая часть энергии отражается обратно к генератору. Коэффициент отражения зависит от соотношения фазовой скорости волны в раскрыве рупора и фазовой скорости волны в свободном пространстве (т.е. скорости света). Если в волноводе фазовая скорость волны равна

, (3.13)

где а – размер широкой стенки волновода, то в раскрыве рупора:

. (3.14)

В Н – секториальном рупоре (рис.3.4) размер L постепенно изменяется от величины «а» в волноводе до L_Н в раскрыве. В соответствии с этим плавно изменяется и фазовая скорость от V_фв до V_фр = с, обеспечивая тем самым хорошее согласование волновода со свободным пространством.

В Е – секториальном рупоре размер L остается неизменным (L= L_Н = в) по всей его длине и поэтому фазовая скорость в таком рупоре остается постоянной и изменяется скачком при переходе волны из рупора в свободное пространство (рис.3.5). Это приводит к отражению значительной части энергии от раскрыва рупора в питающий волновод.

Таким образом, Е – секториальный рупор хуже согласован с волноводом по сравнению с Н – секториальным рупором. Пусть а = 0.7l.

Тогда Ом,

а коэффициент отражения от раскрыва рупора равен

.

Коэффициент бегущей волны в волноводе определится из формулы

КБВ = ,

что существенно меньше по сравнению с Н – секториальным рупором.

Коэффициент направленного действия,

коэффициент использования поверхности

и коэффициент усиления рупорной антенны

Коэффициент направленного действия любой реальной поверхностной антенны, в том числе и рупорной, определяется по формуле:

, (3.15)

где s – геометрическая площадь поверхности раскрыва антенны,

Величина n определяется неравномерностью распределения амплитуды и фазовыми искажениями в раскрыве рупора. Чем больше поля вторичных источников в центре раскрыва и на краю отличаются по амплитуде и фазе, тем меньше значение КИП и соответственно меньше КНД.

В оптимальных рупорах n = 0,61. В случае, когда размеры рупоров отличны от оптимальных, коэффициент направленного действия пирамидального рупора может быть выражен из условия:

, (3.16)

где L_E – размер раскрыва в плоскости Е,

L_H – размер раскрыва в плоскости Н,

D_E – КНД Е – секториального рупора.

Рис.3.6. Определение КНД Н-секториального рупора	Рис.3.7. Определение КНД Е-секториального рупора

На рис.3.6 и на рис.3.7 изображены семейства кривых, показывающих зависимость КНД Н – секториального и Е – секториального рупоров от их размеров. Из рисунков следует, что с увеличением раскрыва при неизменной длине рупора КНД сначала возрастает, достигая максимума, а затем уменьшается. При этом величина максимума увеличивается с ростом длины рупора R. Под длиной рупора R подразумевается расстояние по нормали от плоскости ракрыва до горловины рупора (рис.3.3).

Произведение Sn называется эффективной площадью антенны, т.е.

, (3.17)

Отсюда . (3.18)

Понятие эффективной площади имеет общий характер и может быть распространено на антенны любых типов (одиночные вибраторы, антенные решетки, поверхностные антенны). Исходя из общих позиций эффективную площадь антенны можно определить как некоторую воображаемую часть фронта плоской электромагнитной волны, через которую проходит вся мощность, извлекаемая приемной антенной из окружающего пространства. Это понятие справедливо и для передающей антенны, так как и приемная и передающая антенны имеют идентичные электрические характеристики. Особенно удобно этот параметр вводить в случае поверхностных антенн (излучающих поверхностей). В этом случае эффективную площадь антенны можно определить как площадь эквивалентной по излучаемой мощности антенны, у которой амплитуда и фаза поля по раскрыву постоянные. Отсюда непосредственно вытекает, что эффективная площадь раскрыва у реальных антенн меньше геометрической площади, а коэффициент использования поверхности n всегда меньше единицы.

Коэффициент усиления рупорной антенны связан с коэффициентом направленного действия соотношением

где D – коэффициент направленного действия;

G_A – коэффициент усиления;

Практически на СВЧ h » 1 и G_А = D.

Измерение коэффициента усиления антенны

методом сравнения (замещения)

Метод сравнения чаще всего применяется при лабораторных измерениях антенн.

. (3.20)

В качестве эталонной антенны в лабораторной работе используется пирамидальный рупор 2.

Процесс измерений выполняется следующим образом. Вначале в режиме передачи устанавливается эталонный рупор и с помощью аттенюатора, включенного последовательно с рупором, подбирается уровень сигнала на индикаторе приемника, удобный для измерений. Затем вместо эталонного рупора устанавливается исследуемый рупор и аттенюатором восстанавливается прежний уровень на индикаторе приемника. Коэффициентом усиления рупора будет величина, равная отношению показаний по шкале аттенюатора (в разах) DU, умноженная на коэффициент усиления эталонной антенны. В децибелах формула для коэффициента исследуемого рупора имеет вид:

Коэффициент усиления эталонного рупора определяется по формуле (3.16).

Источник