Чем занимается техническая механика

Техническая механика

Что такое Техническая механика?

Учебная дисциплина «Техническая механика», изучаемая студентами Каменского агротехнического техникума в пределах рабочих программ для технических специальностей, включает следующие разделы:

Теоретическая механика

Раздел «Теоретическая механика» состоит из подразделов:

«Статика» является частью Теоретической механики, изучающей условия, при которых тело находится в равновесии. При этом равновесием считается такое состояние тела, когда оно находится в покое или движется прямолинейно и равномерно.
Методы и приемы, применяемые для решения задач Статики, позволяют определить внешние силовые факторы, благодаря которым тело находится в состоянии равновесия, т. е. по известным значениям внешних сил или моментов, приложенных к телу, осуществить расчет неизвестных силовых факторов (сил, моментов), воздействующих на данное тело.
Выполнение таких расчетов необходимо для осуществления оценки работоспособности конструкций различных сооружений или механизмов при помощи методов и приемов, применяемых в науке «Сопротивление материалов».

«Кинематика» является частью Теоретической механики, и изучает законы движения материальных тел без учета силовых факторов, вызывающих это движение, т. е. с геометрической точки зрения.
Задачи Кинематики сводятся к определению положения тела в пространстве относительно какой-либо системы отсчета в определенный момент времени или через временной промежуток.
Методы и приемы, применяемые при решении задач Кинематики, позволяют производить кинематические расчеты сложных механизмов машин, в которых отдельные детали и узлы совершают относительные перемещения при работе.

«Динамика», в отличие от Кинематики, изучает законы движения материальных тел с учетом силовых факторов, вызывающих это движение.
Методы и приемы, применяемые в Динамике, позволяют производить расчеты движения и перемещения деталей, узлов и механизмов машин, вызываемых приложенными нагрузками и реакциями.

Сопротивление материалов

Детали и механизмы машин

Раздел «Детали и механизмы машин» является прикладным разделом Технической механики. Он изучает возможность практического применения методов и приемов Теоретической механики и Сопротивления материалов при конструировании и проектировании машин, механизмов, сооружений и других инженерных конструкций.

Структура раздела «Детали машин» складывается из составных частей, включающих основные понятия о надежности и работоспособности машин и механизмов, классификацию видов соединений деталей, их свойства и особенности с точки зрения сопротивления материалов, типы и виды механизмов (муфты, опоры, передачи, редукторы и т. п.), а также изучение методов расчета соединений и механизмов по основным критериям работоспособности.

В высших технических учебных заведениях разделы «Сопромат» и «Детали машин» выделены в отдельные предметы, изучаемые студентами по углубленным программам. Обучающимся техническим специальностям среднего профессионального образования (СПО) эти предметы обычно преподаются по упрощенным программам и объединяются в разделы общего курса Технической механики.

Билеты для проверки усвоения знаний при промежуточной аттестации по разделу «Детали машин» можно скачать здесь (документ в формате Word, 600 кБ)

Методические рекомендации и контрольные задания для студентов заочных отделений технических и машиностроительных специальностей:

Примечание: Документы размещены в формате Word, и могут быть сохранены на компьютере или распечатаны на принтере.

Экзаменационные вопросы по Технической механике для студентов:

Источник

Черчение

Общие сведения

Достижения технической механики позволяют не только улучшать кон­струкции машин и механизмов, но и совершенствовать производственные процессы. Сегодня на многих предприятиях широко используются маши­ны-автоматы, автоматические поточные линии, которые без прямого учас­тия человека обеспечивают выпуск готовой продукции, начиная с обработ­ки сырья и кончая упаковкой готовых изделий.

Область применения законов механики для решения конкретных техни­ческих задач очень обширна. Наша эпоха научно-технического прогресса с особенной силой подтверждает необозримость практического приложения этой науки.

Техническая механика — это наука об общих законах меха­нического движения и применения их в современной технике.

Техническая механика состоит из двух частей: теоретичес­кой и прикладной. Первая часть посвящена изучению теоретических основ механического движения, вторая — использованию положений теоретиче­ской механики для практических целей: проектирования механизмов, рас­чета деталей машин, строительных конструкций и сооружений.

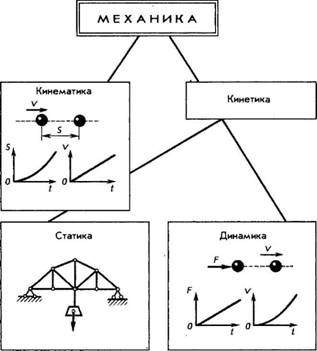
Теоретическую механику принято подразделять на три тесно связанных раздела: статику, кинематику и динамику (рис. 1). В за­дачи теоретической механики входит определение условий, при которых соблюдаются условия равновесия тел. Этот раздел механики называют статикой. Изучением движения тел на основании законов геометрии занимается раздел механики, называемый кинематикой. Раздел ме­ханики, в котором изучается движение тел и рассматриваются причины, его вызвавшие, называют динамикой. Статика, кинематика и динами­ка охватывают все вопросы, связанные с механическим движением тел, и позволяют решать многочисленные практические задачи.

Понятие «тело» является обобщающим. В механике под телом принято понимать все предметы окружающего нас мира: строения, оборудование це­хов заводов, лабораторий и т. д. Твердое тело — физическое тело, характеризующееся стабильностью формы. Механическим движением тела называется изменение его положения по отношению к другим телам с течением времени.

Прикладная механика также состоит из трех крупных разделов: тео­рии механизмов и машин, сопротивления материалов, деталей машин.

В «Теории механизмов и машин» на основании законов теоретической механики рассматриваются принципы анализа и проектирования механиз­мов, «Сопротивление материалов» позволяет установить условия прочнос­ти и устойчивости проектируемых конструкций и сооружений. «Детали ма­шин» посвящены изучению принципов расчета и конструирования деталей и сборочных единиц машин общего назначения.

Последовательное изучение всех этих разделов и является предметом технической механики.

Источник

iSopromat.ru

Техническая механика (сокр. — техмех) — часть общей механики, изучающая механическое движение и различные виды взаимодействия материальных тел.

Курс технической механики состоит из разделов:

Для изучения данного курса и успешной сдачи экзаменов на нашем сайте Вы можете:

Содержание разделов технической механики

Лекции по технической механике не вошедшие в данный список можно найти, пройдя по ссылке на соответствующий раздел или воспользовавшись поиском по сайту.

Теоретическая механика

Кинематика

Статика

Динамика

Сопротивление материалов

Теория механизмов и машин

Детали машин

Цели освоения предмета «Техническая механика»

Целью освоения дисциплины «Техническая механика» является обобщение знаний механических дисциплин, необходимых для расчета и конструирования простейших деталей механизмов, приборов, и формирование фундамента для изучения дисциплин профессионального цикла, а также последующего обучения в магистратуре, аспирантуре.

Задания, выдаваемые для самостоятельной работы, способствуют развитию умения пользоваться типовыми методами расчета и проектирования машин.

В сумме со всеми предшествующими дисциплинами «Техническая механика» является завершающим курсом в подготовке бакалавров технологических специальностей.

В результате освоения дисциплины «Техническая механика» студент должен:

Место техмеха в структуре ООП ВПО

Дисциплины, предшествующие изучению данной дисциплины: «Высшая математика», «Физика», «Инженерная графика», «Информатика».

Предметы, для которых освоение данной дисциплины необходимо как предшествующее: «Надежность технических систем и техногенный риск» и другие специальные дисциплины.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Техническая механика

Содержание

Предмет механики и её разделы

Таким образом, по предмету изучения механика подразделяется на:

Другой важнейший признак, используемый при подразделении механики на отдельные разделы, основан на тех представлениях о свойствах пространства, времени и материи, на которые опирается та или иная конкретная механическая теория. По данному признаку в рамках механики выделяют такие разделы:

Механическая система

Механика занимается изучением так называемых механических систем.

Являясь одним из классов физических систем, механические системы по характеру взаимодействия с окружением разделяются на замкнутые (изолированные) и незамкнутые, по принципу изменения свойств во времени — на статические и динамические.

Наиболее важными механическими системами являются:

Важнейшие механические дисциплины

Стандартные («школьные») разделы механики: кинематика, статика, динамика, законы сохранения. Кроме них, механика включает следующие (во многом перекрывающиеся по содержанию) механические дисциплины:

Некоторые курсы механики ограничиваются только твёрдыми телами. Изучением деформируемых тел занимаются теория упругости (сопротивление материалов — её первое приближение) и теория пластичности. В случае, когда речь идёт не о жёстких телах, а о жидкостях и газах, необходимо прибегнуть к механике жидкостей и газов, основными разделами которой являются гидростатика и гидрогазодинамика. Общей теорией, изучающей движение и равновесия жидкостей, газов и деформируемых тел, является механика сплошных сред.

Основной математический аппарат классической механики: дифференциальное и интегральное исчисление, разработанное специально для этого Ньютоном и Лейбницем. К современному математическому аппарату классической механики относятся, прежде всего, теория дифференциальных уравнений, дифференциальная геометрия (симплектическая геометрия, контактная геометрия, тензорный анализ, векторные расслоения, теория дифференциальных форм), функциональный анализ и теория операторных алгебр, теория катастроф и бифуркаций. В современной классической механике используются и другие разделы математики. В классической формулировке, механика базируется на трёх законах Ньютона. Решение многих задач механики упрощается, если уравнения движения допускают возможность формулировки законов сохранения (импульса, энергии, момента импульса и других динамических переменных).

Различные формулировки механики

Все три закона Ньютона для широкого класса механических систем (консервативных систем, лагранжевых систем, гамильтоновых систем) связаны с различными вариационными принципами. В этой формулировке классическая механика таких систем строится на основе принципа стационарности действия: системы движутся так, чтобы обеспечить стационарность функционала действия. Такая формулировка используется, например, в лагранжевой механике и в гамильтоновой механике. Уравнениями движения в лагранжевой механике являются уравнения Эйлера — Лагранжа, а в гамильтоновой — уравнения Гамильтона.

Независимыми переменными, описывающими состояние системы в гамильтоновой механике, являются обобщённые координаты и импульсы, а в механике Лагранжа — обобщённые координаты и их производные по времени.

Если использовать функционал действия, определённый на реальной траектории системы, соединяющей некую начальную точку с произвольной конечной, то аналогом уравнений движения будут уравнения Гамильтона — Якоби.

Следует отметить, что все формулировки классической механики, основанные на голономных вариационных принципах, являются менее общими, чем формулировка механики, основанная на уравнениях движения. Не все механические системы имеют уравнения движения, представимые в виде уравнения Эйлера — Лагранжа, уравнения Гамильтона или уравнения Гамильтона — Якоби. Тем не менее, все формулировки являются как полезными с практической точки зрения, так и плодотворными с теоретической. Лагранжева формулировка оказалась особенно полезной в теории поля и релятивистской физике, а гамильтонова и Гамильтона — Якоби — в квантовой механике.

Классическая механика

Границы применимости классической механики

В настоящее время известно три типа ситуаций, в которых классическая механика перестаёт отражать реальность.

Источник

Основные определения и понятия технической механики

Основные определения и понятия технической механики.

1. Теоретическая механика – это наука о равновесии тел в пространстве, о системах сил, и о переходе одной системы в другую.

2. Сопротивление материалов – наука о расчетах конструкций на прочность, жесткость и устойчивость.

3. Детали машин – это курс, изучающий назначение, классификацию и основы расчета деталей общего типа.

Механические движения – это изменение положения тела в пространстве и во времени.

Материальная точка – это тело, формами и размерами которого можно пренебречь, но которое обладает массой.

Абсолютно твердое тело – это тело, у которого расстояние между любыми двумя точками остается неизменным при любых условиях.

Сила – мера взаимодействия тел.

Сила – векторная величина, которая характеризуется:

1. точкой приложения;

2. величиной (модулем);

1. Изолированная точка – это материальная точка, которая под действием сил движется равномерно прямолинейно, либо находится в состоянии относительного покоя.

2. две силы равны, если они приложены к одному телу, действуют вдоль одной прямой и направлены в противоположные стороны, такие силы называются уравновешивающими.

3. Не нарушая состояния тела к нему можно приложить или от него отбросить уравновешивающую систему сил.

Следствие: всякую силу можно переносить вдоль линии её действия, не изменяя действия силы на данное тело.

4. Равнодействующая двух сил приложенных в одной точке, приложена в той же точке и является по величине и направлению диагональю параллелограмма, построенных на данных силах.

5. Всякому действию есть равное по величине и направлению противодействие.

Связи и их реакции.

Свободное тело – это такое тело, перемещение которого в пространстве ничего не меняет.

Те тела, которые ограничивают перемещение выбранного тела называются связями.

Силы, с которыми связь удерживают тело называются реакциями связей.

При решении задач мысленно связи отбрасываются и заменяются реакциями связей.

1. Связь в виде гладкой поверхности

3. Связь в виде жесткого стержня.

4. Опора в точке или опора углу.

5. Шарнирно подвижная опора.

6. Шарнирно неподвижная опора.

Система сил – это совокупность.

Сходящиеся Параллельные Сходящиеся Параллельные

Плоская система сходящихся сил.

Плоская система сходящихся сил – это система сил линии действия, которых сходятся в одной точке называются сходящимися.

Пусть дана система сходящихся сил F1, F2, F3, линии, действия которых сходятся в точке О. для того, чтобы заменить эту систему сил равнодействующей силой необходимо:

1. Перенести силы в точку О (на основании следствия из аксиом).

2. Почленно сложить вектора сил (на основании аксиомы 4). Равнодействующая всегда направлена из начала первого вектора в конец последней. В результате векторного сложения образуется силовой многоугольник.

Плоская система сходящихся сил имеет два условия равновесия:

1. Геометрическое условие: плоская система сходящихся сил находится в равновесии, если силовой многоугольник замкнут, т. е. равнодействующая равна нулю.

2. Аналитическое условие: плоская система сходящихся сил находится в равновесии если алгебраические суммы проекций всех сил системы на оси х и у равны нулю.

Пара сил – это система двух равных сил, лежащих на параллельных прямых и направленных в противоположные стороны.

Действие пары на тело определяется моментом на пару.

Момент – это произведение модуля силы на плечо.

Плечо – кратчайшее расстояние между линиями действия силы.

Если пара поворачивает плечо по ходу часовой стрелки, то момент считается положительным, а если против хода, то отрицательным.

Пара сил обладает свойствами:

1. не нарушая действия пары на тело можно её переносить в любую точку плоскости.

2. Две пары сил являются эквивалентными, если их моменты равны.

Система пар сил находится в равновесии, если сумма моментов всех пар системы равно нулю.

Произвольная плоская система сил.

Момент силы относительно точки.

Плечо – это кратчайшее расстояние от выбранной точки до линии действия силы.

Момент силы относительно точки может быть равен нулю, если сила проходит через выбранную точку.

Между моментом пары и моментом силы есть разница: момент пары есть величина постоянная, а момент силы относительно точки по знаку зависит от выбора точки.

Три формы равновесия произвольной плоской системы сил.

1. Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси х и у равны нулю, а также равна нулю сумма моментов всех сил относительно любой точки.

2. Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на одну из осей х или у равна нулю, а также, если равны нулю алгебраические суммы моментов всех сил относительно любых двух точек.

3. Произвольная плоская система сил находится в равновесии, если алгебраические суммы моментов всех сил относительно любых трех точек, не лежащих на одной прямой.

Пространственная система сил.

Пространственная система сил – это система сил, как угодно расположенных в пространстве.

Суммой трех сил, сходящихся в одной точке является сила по величине и направлению, совпадающая с диагональю параллелепипеда, построенного на заданных силах.

Момент силы относительно оси равен произведению модуля силы на кратчайшее расстояние от выбранной оси до линии действия силы.

Момент может равняться нулю, если:

1. Сила лежит на выбранной оси.

2. Сила пересекает выбранную ось.

3. Сила параллельна оси.

При приведении пространственной системы сил к точке, её можно заменять на эквивалентную систему с главным вектором и главным моментом.

Главный вектор – это геометрическая сумма всех сил системы.

Главный момент – это сумма моментов, компенсирующих пар.

Пространственная система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси x, y, z равны нулю, а также равны нулю моменты всех сил относительно этих же осей.

Кинематика изучает виды движения.

Плоско – параллельное движение.

Плоско – параллельное движение – это такое движение, при котором фигура полученная пересечением данного тела с выбранной плоскостью остается параллельной самой себе за все время движения.

При плоско – параллельном движении всегда существует точка, абсолютная скорость которой в данный момент времени равна нулю. Каждый последующий момент – это будет другая точка.

Динамика изучает виды движения тела в зависимости от приложенных сил.

1. всякая изолированная точка находится в состоянии относительного покоя, или равномерного прямолинейного движения до тех пор, пока приложенные силы не выведут её из этого состояния.

2. Ускорение тела прямопропорциональных действующей на тело силе.

3. Если на тело действует система сил, то его ускорение будет складываться из тех ускорений, которые бы тело получало от каждой силы в отдельности.

4. Всякому действию есть есть равное по величине и противоположно направлению противодействие.

Центр тяжести – это точка приложения силы тяжести, при повороте тела центр тяжести не меняет своего положения.

Сила инерции – всегда направлена в противоположную сторону ускорению и приложена к связи.

При равномерном движении, т. е. когда а=0 сила инерции равна нулю.

При криволинейном движении раскладывается на две составляющие: на нормальную силу и на касательную.

Метод кинематики: условно прикладывают к телу силу инерции можно считать, что внешние силы реакции связей и сила инерции образуют уравновешенную систему сил. F+R+Pu=0

Трение делится на два вида: трение скольжения и трение качения.

Законы трения скольжения:

1. Сила трения прямопропорциональной нормальной реакции опоры и направлена вдоль соприкасающихся поверхностей в противоположную сторону движению.

2. Коэффициент трения покоя всегда больше коэффициента трения движения.

3. Коэффициент трения скольжения зависит от материала и физически – механических свойств трущихся поверхностей.

Трение приводит к снижению срока службы деталей к их износу и нагреву. Для того, чтобы этого избежать необходимо вести смазку. Повысить качество обработки поверхности деталей. В трущихся местах применять другие материалы.

4. По возможности заменить трение скольжения трением качения.

Сопротивление материалов – это наука, изучающая методы расчета конструкций на прочность, жесткость и устойчивость.

Прочность – это способность конструкции выдерживать заданную нагрузку в течение срока службы без разрушения и появления остаточных деформаций.

Жесткость – это способность конструкции сохранять первоначальную форму упругого равновесия.

Устойчивость – это способность конструкции сохранять первоначальную форму упругого равновесия.

Все тела разделены на 3 группы:

1. Брус – это тело, один из размеров которого (длина) во много раз больше двух других.

2. Оболочка – это тело, один из размеров которого (толщина) во много раз больше двух других.

3. Массив – это тела, все размеры которого равны.

1. По характеру действия:

2. По способу приложения:

Мысленно разрезаем нагруженный силами груз, для того, чтобы определить внутренние силовые факторы, для этого отбрасываем одну часть груза. Заменяем межмолекулярную систему сил эквивалентной системой с главным вектором и главным моментом. При разложении главного вектора и главного момента по осям x, y, z. устанавливаем вид деформации.

Внутри сечения бруса может возникать внутри силовых факторов, если возникает сила N (продольная сила), то брус растянут или сжат.

Если возникает Мк (крутящий момент) то деформация кручения, сила Q (поперечная сила) то деформация сдвига среза или изгиба. Если возникает Мих и Миz (изгибающий момент) то деформация изгиба.

Метод сечения позволяет определить напряжение в сечении груза.

Напряжение – это величина, показывающая, сколько нагрузки приходится на единицу площади сечения.

Эпюра – это график изменения продольных сил, напряжений, удлинений, крутящих моментов и т. д.

Растяжение (сжатие) – это такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила.

Правила знаков для нагрузки.

Если нагрузка направлена от сечения бруса, то продольная сила будет равна ей со знаком «плюс», если нагрузка направлена к сечению, то продольная сила будет со знаком «минус».

В пределах упругих деформаций нормальное напряжение прямо – пропорционально продольным деформациям.

Е – модуль Юнка, коэффициент, который характеризует жесткость материала при напряжениях, зависит от материала, образца из справочных таблиц.

Нормальное напряжение измеряется в Паскалях.

Расчет на прочность.

np – расчетный коэффициент запаса прочности.

[n] – допустимый коэффициент запаса прочности.

бmax – расчет максимального напряжения.

Кручение – такой вид деформации, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор – крутящий момент. Кручению повергаются валы, оси. И пружины. При решении задач строятся эпюры крутящих моментов.

Источник