Формула стерджесса для чего
Определение величины интервала. Формула Стерджесса.
Статистическим распределением выборки.
Статистическим распределением выборкиназывают перечень вариант и соответствующих им частот (или относительных частот).
Статистическое распределение выборки
| Варианты хi | x1 | x2 | x3 | … | xi | … | xk |
| Число наблюдений (частота) ni | n1 | n2 | n3 | … | ni | … | nk |
| Относительная частота Pi | P1 | P2 | P3 | … | Pi | … | Pk |
Интервальными называются вариационные ряды, в которых значения признаков, положенных в основу их образования, выражены в определенных пределах (интервалах). Частоты в этом случае относятся, не к отдельным значениям признака, а ко всему интервалу.
Интервальные ряды распределения строятся по непрерывным количественным признакам, а также по дискретным признакам, варьирующим в значительных пределах.
Интервальный ряд можно представить статистическим распределением выборки с указанием интервалов и соответствующих им частот. При этом в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал.
При группировке по количественным непрерывным признакам важное значение имеет определение размера интервала.
Определение величины интервала. Формула Стерджесса.

Часто строят ряды с равновеликими интервалами. При построении вариационного ряда с равными интервалами определяют число групп (к) и величину интервала (h).
Оптимальное число групп (интервалов) может быть определено по формулеСтерджесса:
Сами интервалы могут быть закрытыми(с указанием нижней и верхней границ) и открытыми(с указанием лишь одной из границ интервала).
При количественных группировках следует обращать внимание на правильное обозначение нижней и верхней границ интервала. При образовании интервалов по дискретным признакам это достигается посредством обозначения верхней и нижней границ смежных интервалов значениями признаков, отличных на единицу.
При построении интервальных вариационных рядов по непрерывным признакам необходимо указать, в какой интервал входит значение признака, являющегося границей смежных интервалов. То есть для устранения неопределенности необходимо решить вопрос о том, считать ли верхние границы каждой группы «включительно» или «исключительно».
После того как в результате сводки, материал статистического наблюдения сгруппирован, он, как правило, представляется в виде таблиц.
Статистическая таблица (подлежащее статистической таблицы, сказуемое статистической таблицы, групповая таблица, комбинационная таблица, простая таблица, сложная таблица).
Статистическая таблица— форма наиболее рационального, наглядного и систематического изложения числовых результатов сводки и группировки статистических, материалов в виде ряда строк и столбцов. Основными элементами статистической таблицы являются подлежащее и сказуемое.
В зависимости от характера построения подлежащего различают простые, групповые и комбинационные таблицы.
Простой называется таблица, в подлежащем которой содержится перечень объектов наблюдения, например перечень работников предприятия.
Групповойназывается таблица, в подлежащем которой объекты наблюдения разгруппированы по одному признаку, например по профессиям работников предприятия. Комбинационной называется таблица, в подлежащем которой объекты наблюдения разгруппированы по двум и более признакам в комбинации, например, по категориям работников, в том числе и по полу.
По структуре сказуемого различают простые и сложные таблицы.
Простая таблицапредусматривает разработку показателей, характеризующих изучаемые объекты независимо друг от друга.
Сложная таблица предусматривает разработку показателей, характеризующих изучаемые объекты в комбинации.
Например, при характеристике объема перевозок в сказуемом таблицы можно дать перечень признаков, характеризующих объем перевозок по типам тяги и по видам движения. Это будет таблица с простой разработкой сказуемого.
Можно построить таблицу, сказуемое которой будет содержать перечень признаков по типам тяги и в том числе по видам движения. Это будет таблица со сложной разработкой сказуемого.
Наряду с таблицами, для наглядного изображения данных наблюдения и сводки, в статистике используются графики.
Статистика. Статистическое наблюдение.
Статистика. Статистическое наблюдение.
Вопросы
Задай свой вопрос по этому материалу!
Поделись с друзьями
Комментарии преподавателя
Наблюдаемые значения xi есть варианты, а последовательность вариант, записанных в возрастающем порядке, есть вариационный ряд. Числанаблюдений ni, есть частоты, а их отношение к объему выборки 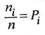
Вариационные ряды распределения подразделяются на дискретные и интервальные.
Дискретными называются вариационные ряды, в которых значения признаков, положенных в основу их образования, являются дискретными; и часто выражены целыми числами. Примерами дискретных вариационных рядов являются распределение рабочих по тарифному разряду; распределение отделов по числу работников и т.п.
Дискретные ряды распределения строятся по дискретным признакам, которые варьируются в ограниченных пределах.
Дискретный ряд распределения обычно оформляется в виде статистического распределения выборки.
2. Статистическим распределением выборки называют перечень вариант и соответствующих им частот (или относительных частот).
Статистическое распределение выборки
| Варианты хi | x1 | x2 | x3 | … | xi | … | xk |
| Число наблюдений (частота) ni | n1 | n2 | n3 | … | ni | … | nk |
| Относительная частота Pi | P1 | P2 | P3 | … | Pi | … | Pk |
Интервальными называются вариационные ряды, в которых значения признаков, положенных в основу их образования, выражены в определенных пределах (интервалах). Частоты в этом случае относятся, не к отдельным значениям признака, а ко всему интервалу.
Интервальные ряды распределения строятся по непрерывным количественным признакам, а также по дискретным признакам, варьирующим в значительных пределах.
Интервальный ряд можно представить статистическим распределением выборки с указанием интервалов и соответствующих им частот. При этом в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал.
При группировке по количественным непрерывным признакам важное значение имеет определение размера интервала.
3. Величина интервала— разность между наибольшим и наименьшим значениями признака в каждой группе, называемыми границами интервала.
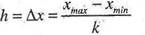
Часто строят ряды с равновеликими интервалами. При построении вариационного ряда с равными интервалами определяют число групп (к) и величину интервала (h).
Оптимальное число групп (интервалов) может быть определено по формуле Стерджесса:
K=1+3.322 lg n,
Сами интервалы могут быть закрытыми(с указанием нижней и верхней границ) и открытыми(с указанием лишь одной из границ интервала).
При количественных группировках следует обращать внимание на правильное обозначение нижней и верхней границ интервала. При образовании интервалов по дискретным признакам это достигается посредством обозначения верхней и нижней границ смежных интервалов значениями признаков, отличных на единицу.
При построении интервальных вариационных рядов по непрерывным признакам необходимо указать, в какой интервал входит значение признака, являющегося границей смежных интервалов. То есть для устранения неопределенности необходимо решить вопрос о том, считать ли верхние границы каждой группы «включительно» или «исключительно».
После того как в результате сводки, материал статистического наблюдения сгруппирован, он, как правило, представляется в виде таблиц.
4. Статистическая таблица— форма наиболее рационального, наглядного и систематического изложения числовых результатов сводки и группировки статистических, материалов в виде ряда строк и столбцов. Основными элементами статистической таблицы являются подлежащее и сказуемое.
В зависимости от характера построения подлежащего различают простые, групповые и комбинационные таблицы.
Простой называется таблица, в подлежащем которой содержится перечень объектов наблюдения, например перечень работников предприятия.
Групповойназывается таблица, в подлежащем которой объекты наблюдения разгруппированы по одному признаку, например по профессиям работников предприятия. Комбинационнойназывается таблица, в подлежащем которой объекты наблюдения разгруппированы по двум и более признакам в комбинации, например, по категориям работников, в том числе и по полу.
По структуре сказуемого различают простые и сложные таблицы.
Простая таблицапредусматривает разработку показателей, характеризующих изучаемые объекты независимо друг от друга.
Сложная таблица предусматривает разработку показателей, характеризующих изучаемые объекты в комбинации.
Например, при характеристике объема перевозок в сказуемом таблицы можно дать перечень признаков, характеризующих объем перевозок по типам тяги и по видам движения. Это будет таблица с простой разработкой сказуемого.
Можно построить таблицу, сказуемое которой будет содержать перечень признаков по типам тяги и в том числе по видам движения. Это будет таблица со сложной разработкой сказуемого.
Наряду с таблицами, для наглядного изображения данных наблюдения и сводки, в статистике используются графики.
5. Графическим способом изображения статистических данных называют их условное изображение при помощи точек, линий, плоскостей, геометрических фигур и условных знаков. Графики в статистике применяются для: сравнения одноименных показателей, относящихся к различным объектам; наглядного представления структуры совокупности и ее изменения; характеристики динамики и степени распространения явления; отображения взаимосвязи явлений.
В зависимости от назначения используют различные виды графиков: линейные, столбиковые, ленточные, секторные, фигурные.
Линейные диаграммыобычно применяют для характеристики динамики явлений, их взаимосвязи.
Столбиковые, ленточные диаграммыиспользуются для сравнения значений статистических показателей, характеризующих изучаемые объекты в разные моменты времени (за разные периоды времени).
Секторные диаграммыиспользуются для характеристики структуры совокупности.
Фигурные диаграммыиспользуют при сравнении различных явлений по степени их распространения.
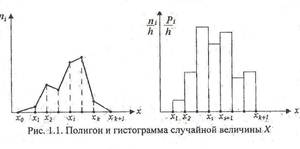
Дискретные вариационные ряды изображают в виде полигона (многоугольника) распределения.
Полигон распределения строится в прямоугольной системе координат. На оси абсцисс откладываются варианты, а на оси ординат наносится шкала частот. На оси абсцисс отмечаются точки, соответствующие величинам вариант, и из них восстанавливаются перпендикуляры, длины которых соответствуют частотам конкретных вариант. В результате соединения концов перпендикуляров отрезками прямой, получают полигон распределения. При этом первую точку следует соединить с точкой на оси абсцисс, соответствующей предшествующей варианте, частота которой равна нулю. Последнюю точку следует также соединить с точкой на оси абсцисс, соответствующей варианте, следующей за последней (частота ее также равна нулю). Таким образом получается многоугольник, изображающий распределение признака (рис. 1.1).
Интервальный ряд графически изображается в виде гистограммы (клеточного графика) распределения.
Если частоты отнести к серединам интервалов и соединить ординаты прямыми, то получится полигон распределения.
Источник видео: https://www.youtube.com/watch?v=rpbYIciRzpU
Источник конспекта: http://studopedia.ru/2_87781_graficheskiy-sposob-izobrazheniya-statisticheskih-dannih.html
Файлы
Нет дополнительных материалов для этого занятия.
Памятка по экономическим формулам
Среднее арифметическое (простое среднее 1-го порядка)
Простая средняя 1-го порядка (среднее арифметическое) применяется для определения наиболее вероятного значения нормально распределенного числового ряда и является важнейшим понятием в математической и прикладной статистике. Кстати, случай, описанный в бородатом анекдоте про температуру в больнице, для средней арифметической величины неприменим, поскольку распределение здесь не является нормальным. В «случае с больницей» необходимо применять цензурирование данных или т.н. структурные средние
Простая средняя 1-го порядка расчитывается по формуле
хi – значение признака;
n – обьем совокупности;В MS Excel для вычисления среднего арифметического применяется функция СРЗНАЧ().
Среднее арифметическое взвешенное
Наряду с простой средней арифметической величиной применяют и среднюю арифметическую взвешенную, которую используют, когда, к примеру, значения вариантов встречаются по нескольку раз или каждое значение ряда имеет какой-то определенный индивидуальный вес:
хi — элементы признака;
Среднее гармоническое
хi — элементы признака;
fi— частота или вес i-го признака (равен 1 для простого гармонического среднего).
Среднее геометрическое
Среднее геометрическое применяется, к примеру, в тех случаях, когда имеется n коэффициентов роста, а индивидуальные значения признака представляют собой относительные показатели динамики, достроенные в виде цепных величин (как отношение к предыдущему уровню). Этот вид срднего характери¬зует средний коэффициент роста и рассчитывается по формуле:
хi – значение признака;
Среднее геометрическое взвешенное
Среднее геометрическое взвешенное при абсолютных значениях уровней ряда (простое среднее геометрическое применяется при текущих коэффициентах или темпах роста).Формула среднего геометрического взвешенного имеет следующий вид:
хi — элементы признака;
fi— частота i-го признака.
Индекс Герфиндаля (Херфинделя)
Индекс Герфиндаля (Херфинделя) показывает степень рыночной концентрации
Модифицированный индекс Герфиндаля, более удобный для практического применения рассчитывается по формуле:
Индекс Джини
Индекс Джини численно равен площади под кривой Лоренца (залитая область на рис.). Очевидно, что он может принимать значения от 0 до 1, и будет отражать степень неравномерности распределения.
Формула Стерджесса
Оценка оптимального количества групп с равными интервалами для нормальных распределений по формуле Стерджесса:
Размер интервала частот
Для группировок с равными интервалами величина интервала составляет:
Если в результате деления получится дробное число и возникнет необходимость в округлении, то округлять нужно, как правило, в большую сторону.
Точка безубыточности
Определение рекламного бюджета в процентах от объемов прдаж
В этом методе объем рекламного бюджета оценивается относительно реально существующего на данный момент объема прдаж компании:
Определение объема рекламного бюджета с учетом целей и задач
Rb = p * n0 * S / S max,
Рекламный бюджет по формуле Юла
Rb = p * n0 * ( 1 / ( k0 * k ) * ( N / N max ),
Рекламный бюджет по формуле Видаля-Вольфа
Текущая стоимость будущих денежных потоков инвестиционного проекта, рассчитанная с учетом дисконтирования, за вычетом инвестиций. Рассчитывается с использованием прогнозируемых денежных потоков, связанных с планируемыми инвестициями, по следующей формуле:
Для вычисления NPV в среде электронных таблиц MS Excel удобнее всего пользоваться функциями XNPV или ЧИСТНЗ.
Ставка дисконтирования, при которой суммарная приведенная стоимость доходов от осуществляемых инвестиций равна стоимости этих инвестиций. Определяет максимальную стоимость привлекаемого капитала, при которой инвестиционный проект остается выгодным. В другой формулировке, это средний доход на вложенный капитал, обеспечиваемый данным инвестиционным проектом, т.е. эффективность вложений капитала в данный проект равна эффективности инвестирования под IRR процентов в какой-либо финансовый инструмент с равномерным доходом. IRR рассчитывается как значение ставки дисконтирования, при которой NPV=0. Как правило, значения IRR находят либо графическими методами (построив график зависимости NPV от ставки дисконтирования), либо с помощью специализированных программ. В MS Excel для расчета IRR используется функция XIRR или ВНДОХ. IRR не всегда может быть корректно получен из уравнения NPV=0, при определенных значениях денежных потоков это уравнение может не иметь решений или иметь несколько решений. В таких ситуациях IRR проекта считается неопределенным. Для того, чтобы исключить эти сложности, иногда используется модифицированная внутренняя норма рентабельности, хотя этот показатель распространен значительно меньше, чем IRR.
Вариант показателя IRR, модифицированный таким образом, чтобы устранить возможные неопределенности при расчетах. Характеризует ставку дисконтирования, при которой суммарная приведенная стоимость доходов от осуществляемых инвестиций равна стоимости этих инвестиций. Поскольку метод, используемый для расчета IRR, иногда приводит к неопределенностям, модифицированное значение IRR рассчитывается несколько иначе.Методика расчета:
1. Все значения доходов, формируемых инвестициями, приводятся к концу проекта. Для приведения используется ставка, равная средневзвешенной стоимости капитала (WACC).
2. Все инвестиции и реинвестиции приводятся к началу проекта. Для приведения используется ставка дисконтирования.
3. MIRR определяется как норма дохода, при которой все ожидаемые доходы, приведенные к концу проекта, имеют текущую стоимость, равную стоимости всех требуемых затрат:
ПОСТРОЕНИЕ С ПОМОЩЬЮ ФОРМУЛЫ СТЕРДЖЕССА
При использовании электронно-вычислительных машин и персональных компьютеров для обработки статистических данных группировка единиц объекта проводится с помощью стандартных процедур.
Одна из таких процедур основана на использовании следующей формулы Стерджесса для определения оптимального числа групп:
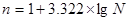
где n – число групп;
N – число единиц совокупности.
Построим группировку с помощью данного метода для таблицы 1.2. Для этого:
1. данные таблицы 1.2 проранжируем и представим в таблице 3.1:
Ранжированный ряд количества магазинов по розничному товарообороту в республике Калмыкия, млн. руб.
| 121 | 208 | 234 | 234 | 238 | 239 | 256 | 280 | 299 | 309 |
| 341 | 342 | 388 | 390 | 400 | 456 | 547 | 469 | 490 | 555 |
| 560 | 562 | 567 | 653 | 689 | 690 | 743 | 764 | 780 | 789 |
| 863 | 870 | 876 | 877 | 890 | 900 | 1100 | 1234 | 1238 | 1345 |
| 1357 | 1790 | 1800 | 2000 | 2345 | 2369 | 2478 | 2580 | 3567 | 4565 |
| 4609 | 5689 | 5789 | 5909 | 6000 | 7890 | 8776 | 8877 | 9000 | 12098 |
2. определим число групп по формуле Стерджесса:
найдем шаг интервала по формуле:


где h – шаг интервала;
R – размах вариации;
Xmin – минимальное значение признака в совокупности.
h= 

Результаты расчетов сведем в таблицу:
Группировка магазинов по розничному товарообороту в республике Калмыкия, млн. руб.
| Группы магазинов по розничному товарообороту, млн. руб. | Количество магазинов | середина интервалов Xi |
| 121-1814 | 42 | 957 |
| 1814 – 3528 | 7 | 2671 |
| 3528 – 5242 | 2 | 4385 |
| 5242 – 6956 | 4 | 6099 |
| 6956 – 8670 | 2 | 7813 |
| 8670 – 12092 | 3 | 10381 |
Особенностью построения групп является то, что у всех групп имеются закрытые интервалы. Из данной таблицы мы видим, что в интервал (121-1814) входит 42 магазинов, в интервал (1814-3528) входит 7 магазинов, в (3528-5242) 2 магазина, в (5242-6956) 4 магазина, в (6956-8670) 2 магазин, в (8670-12092) 3 магазина.
Построим ряд распределения для таблицы 1.3. Для этого:
1. проранжируем ряд чисел, представленный в таблице 1.3, и представим в таблице 3.3.
Ранжированный ряд транспортных организаций по грузообороту транспорта общего пользования в республике Калмыкия, млн. т. км
| 2.78 | 5.0 | 7.43 | 7.89 | 9.43 | 10.9 | 11.0 | 12 | 12.1 | 12.34 |
| 12.36 | 12.38 | 13.57 | 17.90 | 18 | 18.4 | 20 | 20.8 | 21.1 | 23.4 |
| 23.4 | 23.8 | 23.9 | 23.9 | 23.09 | 25.0 | 25.80 | 28 | 29.9 | 30.9 |
| 33.0 | 34.2 | 34.7 | 38.9 | 39.7 | 45 | 45.6 | 46.09 | 46.9 | 48.0 |
| 49.0 | 55.5 | 56.7 | 56.89 | 57.89 | 59.9 | 60 | 69.0 | 76.4 | 78.0 |
| 78.90 | 80.9 | 87 | 87.6 | 87.8 | 89 | 87.76 | 88.77 | 89.0 | 98.8 |
2.определим число групп по формуле (3.1):
3.найдем шаг интервала по формуле (3.2):
h= 
Результаты расчетов сведем в таблицу:
Группировка транспортных организаций по грузообороту транспорта общего пользования в республике Калмыкия, млн. т. км
| Группы транспортных организаций по грузообороту транспорта общего пользования, млн. т. км | Количество транспортных организаций | середина интервалов, Xi |
| 2.78-16.49 | 13 | 9.63 |
| 16.49-30.21 | 17 | 23.35 |
| 30.21-43.93 | 6 | 37.07 |
| 43.93-57.64 | 9 | 50.79 |
| 57.64-71.36 | 14 | 64.50 |
| 71.36-85.08 | 4 | 78.22 |
| 85.08-98.8 | 7 | 91.94 |
По данной таблице видно, что в интервал (2,78-16,49) входит 13 транспортных организаций; в интервал (16,49-30,21) входит 17 транспортных организаций; в интервал (30,21-43,93) 6 транспортных организаций; в интервал (43,93-57,64) 9 транспортных организаций; в интервал (57,64-71,36) 14 транспортных организаций; в интервал (71,36-85,08) 4 организации; в интервал (85,08-98,8) 7 организаций.