Как сделать диаметр окружности
Как вычислить диаметр окружности?
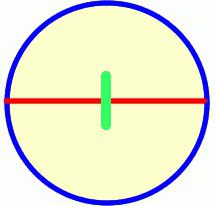
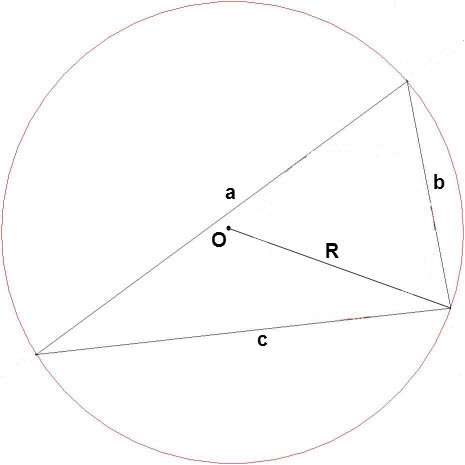
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
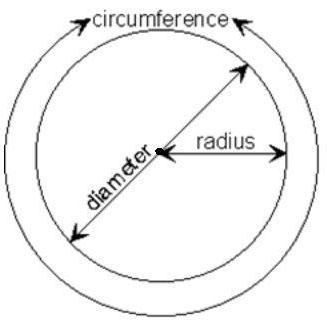
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить длину окружности. Формула L = 2 Пи * R, где 2 – это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
S – в данном случае площадь фигуры. Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
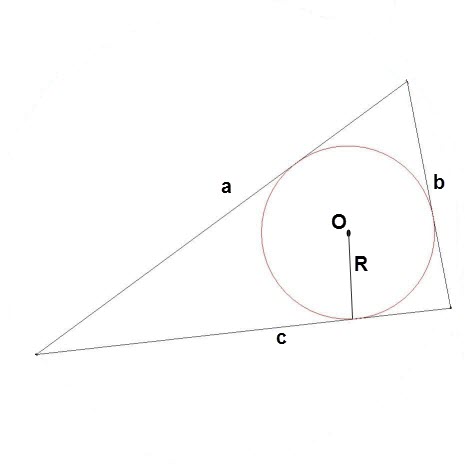
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
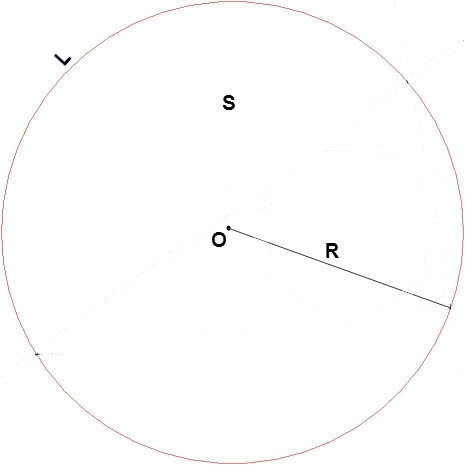
R = S / p (S – площадь заданного треугольника, а p – периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении размера кольца, что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Как вычислить диаметр окружности: формула и пояснения
Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?
Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.
Круг и окружность
Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.
А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.
Что такое длина окружности?
После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.
Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.
Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.
Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.
Формула окружности через диаметр
Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π. Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.
Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π.
Как вычислить диаметр: формула
На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π. Это будет выглядеть так d = C / π.
Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.
Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.
Как вычислить диаметр по длине окружности
Инструкция
2. Сейчас в любом утилитарном случае, когда вам потребуется узнать диаметр какой-то окружности, скажем: крышки на бак, люка, зонтовой крыши, котлована, округлого оврага и так дальше, вы можете, замерив длину окружности, стремительно высчитать ее диаметр.Для этого только нужно применить формулу длины окружности.L = п DЗдесь:L – длина окружности,п – число Пи, равное 3.14,D – диаметр окружности.Переставьте в формуле длины окружности желанное в левую часть и получите:D = L/п
3. Разберем фактическую задачу. Представим, вам нужно изготовить крышку на круглый дачный колодец, доступа к которому в данный момент нет. Не сезон, и неподходящие погодные данные. Но у вас есть данные по длине его окружности. Представим, это 600 см.В указанную формулу подставляем значения:D = 600/3,14 = 191.08 см.Выходит, 191 см составляет диаметр вашего колодца.Увеличивайте диаметр до 2-х метров с учетом припуска за края. Устанавливайте циркуль на радиус 1 м (100 см) и вычерчивайте окружность.
Совет 2: Как узнать диаметр окружности
Инструкция
2. В частных случаях радиус окружности дозволено обнаружить, если она описана либо вписана в треугольник.Если окружность вписана в треугольник, то её радиус находится по формулеR = S/p, где S – площадь треугольника, p = (a + b + c)/2 – полупериметр треугольника.
Совет 3: Как поделить окружность на части
В курсе планиметрии средней школы, представление окружность определяется как геометрическая фигура, состоящая из всех точек плоскости лежащих на расстоянии радиуса от точки, называемой её центром. Внутри окружности дозволено провести уйма отрезков, разным образом соединяющих её точки. В зависимости от построения этих отрезков, окружность дозволено поделить на несколько частей различными методами.
Инструкция
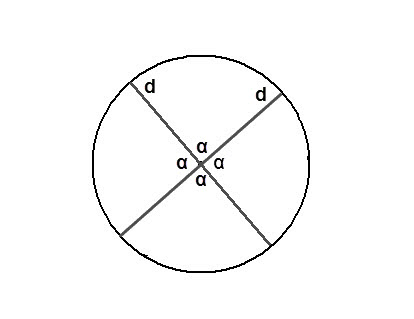
1. Дабы поделить окружность на две равные части, нужно провести её диаметр – отрезок соединяющий точки окружности и проходящий через её центр. С поддержкой диаметров, окружность дозволено поделить на всякое число равных частей, для этого углы между радиусами обязаны быть идентичными.
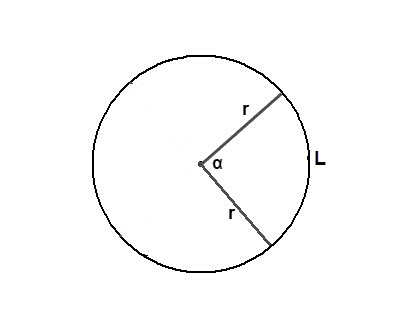
2. Иным методом деления окружности на части является построение секторов. Сектор это часть окружности, состоящая из 2-х радиусов и дуги окружности. Так же как и в случае с диаметрами, с поддержкой секторов окружность дозволено поделить на всякое число равных частей.
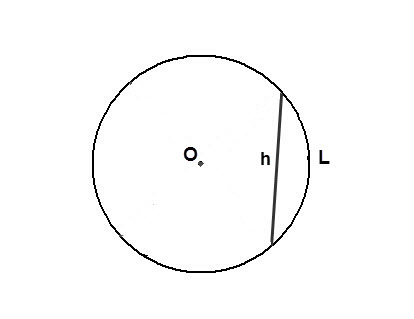
3. Наконец, окружность дозволено поделить построением секций. Сегментом именуется часть окружности, составленная из хорды и дуги окружности. Хордой в этом случае является отрезок, соединяющий всякие две точки окружности. С поддержкой секций окружность дозволено поделить на безмерное уйма частей с образованием либо без многоугольника в его центре.
Видео по теме
Обратите внимание!
Полученные перечисленными методами фигуры – многоугольники, секции и сектора, дозволено также поделить, использую соответствующие способы, скажем, диагонали многоугольников либо биссектрисы углов.
Совет 4: Как вычислить диаметр круга
Кругом называют плоскую геометрическую фигуру, а линию, ее ограничивающую, принято называть окружностью. Основное качество круга заключается в том, что всякая точка на этой линии находится на идентичном расстоянии от центра фигуры. Отрезок с началом в центре круга и окончанием на всякий из точек окружности именуется радиусом, а отрезок, соединяющий две точки окружности и проходящий через центр – диаметром.
Инструкция
1. Обнаружьте длину диаметра круга удвоением длины его радиуса, если эта длина вестима. Это самый примитивный вариант начальных данных при необходимости определить длину диаметра.
2. Используйте число Пи для нахождения длины диаметра по знаменитой длине окружности. Эта константа выражает непрерывное соотношение между этими двумя параметрами круга – самостоятельно от размеров круга, деление длины его окружности на длину диаметра неизменно дает одно и то же число. Из этого вытекает, что для нахождения длины диаметра следует длину окружности поделить на число Пи. Как водится, для фактических вычислений длины диаметра бывает довольно точности до сотых долей единицы, то есть до 2-х знаков позже запятой, следственно число Пи дозволено считать равным 3,14. Но потому что эта константа является числом иррациональным, то имеет безграничное число знаков позже запятой. Если возникнет надобность в больше точном определении диаметра окружности, то необходимое число знаков для числа пи дозволено обнаружить, скажем, по этой ссылке – http://www.math.com/tables/constants/pi.htm.
3. При вестимой площади круга (S) для нахождения длины диаметра (d) удваивайте квадратный корень из отношения площади к числу Пи: d=2∗√(S/π).
4. При вестимой длине стороны описанного вблизи круга прямоугольника, длина диаметра будет равна этой вестимой величине.
5. При вестимых длинах сторон (a и b) прямоугольника, вписанного в круг, длину диаметра (d) дозволено вычислить, обнаружив длину диагонали этого прямоугольника. От того что диагональ тут является гипотенузой в прямоугольном треугольнике, катеты которого образуют стороны вестимой длины, то по теореме Пифагора длину диагонали, а совместно с ней и длину диаметра описанной окружности, дозволено рассчитать, обнаружив квадратный корень из суммы квадратов длин вестимых сторон: d=√(a? + b?).
Совет 5: Как поделить окружность на равные части
Деление окружности на несколько равных частей — зачастую встречающаяся задача. Так дозволено возвести положительный многоугольник, начертить звезду либо подготовить основу для схемы. Есть несколько методов решения этой увлекательной задачи.
Вам понадобится
Инструкция
1. Самый легкой метод поделить окружность на равные части — при помощи транспортира. Поделив 360° на надобное число частей, вы получите угол поворота. Начните с всякий точки на окружности — соответствующий ей радиус будет нулевой отметкой. Начиная с него, делайте по транспортиру отметки, соответствующие вычисленному углу.Данный метод рекомендуется, если вам необходимо поделить окружность на пять, семь, девять и т.д. частей. Скажем, для построения верного пятиугольника его вершины обязаны располагаться через всякие 360/5 = 72°, то есть на отметках 0°, 72°, 144°, 216°, 288°.
Обратите внимание!
Для деления окружности на равные части традиционно используют делительные головки либо делительные столы, дозволяющие поделить окружность на равные части с высокой точностью. Когда нужно поделить окружность на равные части пользуются приведенной ниже таблицей. Для этого необходимо умножить диаметр делимой окружности на показатель, приведенный в таблице: К х D.
Полезный совет
Деление окружности на три, шесть и двенадцать равных частей. Проводят две перпендикулярные оси, которые пересекая окружность в точках 1,2,3,4 делят ее на четыре равные части; Применяя вестимый прием деления прямого угла на две равные части при помощи циркуля либо угольника строят биссектрисы прямых углов, которые пересекаясь с окружностью в точках 5, 6, 7, и 8 делят всякую четвертую часть окружности напополам.
Совет 6: Как узнать диаметр круга
При проведении построений разных геометрических фигур изредка требуется определить их колляции: длину, ширину, высоту и так дальше. Если речь идет о круге либо окружности, то зачастую доводится определять их диаметр. Диаметр представляет собой отрезок прямой, тот, что соединяет две особенно удаленных друг от друга точки, расположенные на окружности.
Вам понадобится
Инструкция
1. В самом простом случае определите диаметр по формуле D = 2R, где R – радиус окружности с центром в точке О. Такая формула комфортна, если вы вычерчиваете круг с заблаговременно оговоренным радиусом. Скажем, если при построении фигуры вы установите раствор ножек циркуля равным 50 мм, то диаметр круга, полученного в итоге, будет равен удвоенному радиусу, то есть 100 мм.
2. Если вам знаменита длина окружности, составляющей внешнюю рубеж круга, то используйте для определения диаметра формулу:D = L / p, гдеL – длина окружности;p – число «пи», равное примерно 3,14.Скажем, если длина окружности равна 180 мм, то диаметр будет равняться примерно: D = 180 / 3,14 = 57,3 мм.
3. Если вы имеете заблаговременно вычерченный круг с незнакомыми радиусом, диаметром и длиной окружности, то для примерного измерения диаметра используйте циркуль и измерительную линейку с делениями. Трудность заключается в том, дабы обнаружить на окружность две точки, максимально вдалеке отстоящие друг от друга, то есть такие, которые будут располагаться именно на диаметре.
4. При помощи линейки проведите прямую линию, дабы она пересекала окружность в любом месте. Точки пересечения линии и окружности подметьте как А и В. Сейчас Установите раствор циркуля таким образом, дабы он был огромнее половины отрезка АВ.
5. Установите иглу циркуля в точку А и проведите дугу, пересекающую отрезок АВ либо даже окружность. Сейчас, не меняя раствор циркуля, установите его в точку В и проделайте то же самое. В итоге вы получите точки пересечения 2-х окружностей по обе стороны от отрезка АВ. Объедините их по линейке прямой линией, дабы она пересекла окружность в точках C и D. Отрезок CD и будет желанным диаметром.
6. Сейчас измерьте диаметр при помощи измерительной линейки, приложив ее к точкам C и D. 2-й метод определения диаметра: приложить ножки циркуля сначала к точкам C и D, а после этого перенести раствор циркуля на измерительную шкалу линейки.
Совет 7: Как по длине окружности узнать диаметр
Определение диаметра окружности может сгодиться не только для решения геометрических задач, но и подмогнуть на практике. Скажем, зная диаметр горлышка банки, вы верно не ошибетесь в выборе крышки для нее. То же заявление объективно и для больше габаритных окружностей.
Инструкция
1. Представим, требуется приобрести крышку для колодца, но точный диаметр вам неведом, а из знаменитых компонентов только длина окружности.
2. Выходит, введите обозначения величин. Пускай d – диаметр колодца, L – длина окружности, п – число Пи, значение которого примерно равно 3,14, R – радиус окружности. Длина окружности (L) вестима. Представим, что она равна 628 сантиметрам.
3. Дальше для нахождения диаметра (d) воспользуйтесь формулой длины окружности: L=2пR, где R – неведомая величина, L=628 см, а п=3,14. Сейчас воспользуйтесь правилом нахождения незнакомого множителя: «Дабы обнаружить незнакомый множитель, необходимо произведение поделить на вестимый множитель». Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
4. Позже того как радиус окружности обнаружен (R=100 см), воспользуйтесь дальнейшей формулой: диаметр окружности (d) равен двум радиусам окружности (2R). Получается: d=2R.
5. Сейчас, дабы обнаружить диаметр, подставьте в формулу d=2R значения и вычислите итог. Потому что радиус (R) вестим, получается: d=2×100, d=200 см.
Полезный совет
Окружности относительно огромных диаметров в домашних условиях комфортно вычерчивать циркулем, тот, что стремительно дозволено изготовить. Делается это так. В рейку вбивается два гвоздя на расстоянии друг от друга, равному радиусу окружности. Один гвоздь неглубоко вбейте в заготовку. А иной используйте, вращая рейку, в качестве маркера.