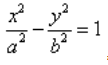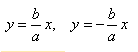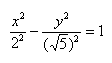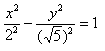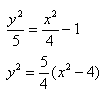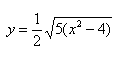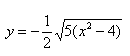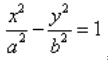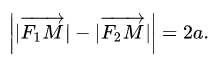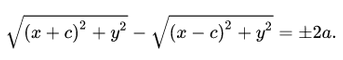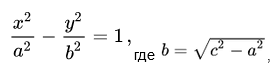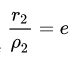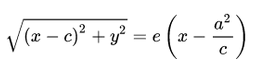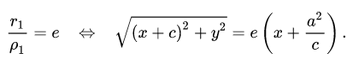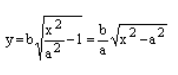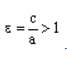Как сделать таблицу гиперболы
Построение графика обратной зависимости – гиперболы (ЕГЭ – 2021)
Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое обратная зависимость.
Давай проверим? Ответь быстро на эти вопросы:
Если что-то из этого забыл, просмотри сначала вот эти темы:
Когда по этим темам все будет понятно, читай далее.
ШПОРА ПРО ГРАФИК ОБРАТНОЙ ЗАВИСИМОСТИ (ГИПЕРБОЛЫ)
Определение
Функция, описывающая обратную зависимость – это функция вида \( \displaystyle y=\frac
График обратной зависимости – гипербола.
Коэффициенты \( \displaystyle k\), \( \) и \( b\).
\( \displaystyle k\) – отвечает за «пологость» и направление графика: чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).
Знак коэффициента \( \displaystyle k\) влияет на то, в каких четвертях расположен график.
Правило построения графика функции \( \displaystyle y=\frac
Обратная зависимость. Функция. Коэффициенты. График
Итак, ты уже умеешь обращаться с обратной зависимостью, анализировать ее график и строить график по точкам.
Напоминаю: обратная зависимость в общем виде задается функцией
\( \displaystyle y=\frac
Давай вкратце вспомним, что делают коэффициенты.
\( \displaystyle k\) – отвечает за «пологость» и направление графика.
Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).
Знак коэффициента \( \displaystyle k\) влияет на то, в каких четвертях расположен график.
— если \( \displaystyle k>0\), то ветви гиперболы расположены в \( \displaystyle I\) и \( \displaystyle III\) четвертях.
— если \( \displaystyle k
Дальше – число \( \displaystyle a\).
Если внимательно посмотреть на знаменатель, видим, что \( \displaystyle a\) – это такое число, которому не может равняться \( \displaystyle x\).
То есть \( x=a\) – это вертикальная асимптота, то есть вертикаль, к которой стремится график (на рисунке выше↑ такой вертикалью является ось \( \displaystyle Oy\)):
ОК, осталось еще одно число: \( \displaystyle b\).
C ним все еще проще: если у нас уже есть гипербола \( \displaystyle y=\frac
То есть нужно просто весь график сместить вверх на \( \displaystyle b\):
Как видим, теперь график стремится по горизонтали к прямой \( y=2\) вместо оси \( Ox\), как было раньше.
Такая прямая называется горизонтальной асимптотой.
Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.
Регистрируйся здесь и приходи!
Принципы построения гиперболы
Теперь давай научимся строить простейшую гиперболу – \( \displaystyle y=\frac
Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.
Например, построим гиперболу \( \displaystyle y=\frac<3>
Составим таблицу из \( 4\) точек, которые принадлежат одной ветке (например, правой):
Отмечаем точки на рисунке:
Проводим через них плавную линию, которая краями приближается к осям:
Это одна ветвь гиперболы.
Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат:
Его автор, Алексей Шевчук, ведет наши курсы подготовки к ЕГЭ по математике и информатике.
Приходи, научишься решать задачи любой сложности с самого нуля. Шаг за шагом.
От 2000 до 3990 руб / месяц, 3 раза в неделю по 2 часа.
Отлично, осталось вспомнить, что собой представляет вторая ветвь?
Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.
Еще один полезный факт.
Для функций, у которых \( k\) – точный квадрат (например, \( 1\), \( 4\) или \( \displaystyle \frac<1><4>\)), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить.
В этом случае достаточно даже трех точек, чтобы построить график.
Например, построим график функции \( \displaystyle y=\frac<4>
Как и в прошлый раз, начнем с правой ветви.
Точка симметрии: \( \displaystyle x=y=2\). Выберем еще одну точку, например, \( \displaystyle x=1\), \( \displaystyle y=4\). У третьей точки координаты будут наоборот: \( \displaystyle x=4\), \( \displaystyle y=1\).
И теперь симметрично отображаем эту ветвь в третью координатную четверть:
Теперь выясним, что будет, если \( \displaystyle k
Ну что же, осталось объединить все то, что мы уже выяснили в один алгоритм:
Алгоритм построения гиперболы
Алгоритм построения графика функции \( \displaystyle y=\frac
Шесть примеров построения графиков гиперболы
Примеры
Решения
Зарегистрируйся один раз и ты откроешь все 100 статей учебника
А также получишь доступ к видеоурокам и другим бесплатным материалам курса «Подготовка к ЕГЭ с репетитором»
* Если не понравятся бесплатные материалы, ты сможешь отписаться в любой момент
Пример 1. Пойдем по порядку по пунктам.
1) \( \displaystyle k=2\); \( \displaystyle a=1\); \( \displaystyle b=1\)
2) \( \displaystyle y=\frac<2>
Пример 2. Сначала преобразуем выражение:
Теперь ясно, что \( \displaystyle k=-1\); \( \displaystyle a=2\); \( \displaystyle b=-1\):
Пример 3.
Пример 4.
\( k=1\), \( a=-3\), \( b=0\). Дополнительное условие \( x\ne 3\) означает, что на графике появится выколотая точка c абсциссой \( x=3\):
Пример 5.
Ты уже, наверное, догадался, что вместо того, чтобы смотреть на эту функцию квадратными глазами и говорить «Что это?!», нужно просто взять и упростить выражение. Если не знаешь, как это делать, то тебе прямая дорога в тему «Преобразование выражений». Да-да, прямо сейчас, все бросай и переходи по ссылке!
Итак, если ты уже усвоил тему «Преобразование выражений», то тебе не составит труда упростить нашу функцию. Вот что должно получиться:
\( \displaystyle k=-\frac<1><2>\), \( \displaystyle a=-\frac<3><2>\), \( b=1\), выколотая точка \( \displaystyle x\ne \frac<5><2>\):
Пример 6. \( \displaystyle y=\frac<2
Здесь нужно не то чтобы упростить, тут нужно привести выражение к виду обратной зависимости.
Мы такие штуки делали в теме «Обратная зависимость»:
Ну вот и все, ты научился строить любую гиперболу.
Замечу также, что правила построения гиперболы оказались немного проще, чем для параболы, ведь каждое число просто сдвигает график в какую-то одну сторону.
И коэффициенты не связаны друг с другом.
P.S. Последний бесценный совет!
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут. Почему? Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем большинство твоих сверстников. Проблема в том, что этого может не хватить…
Для успешной сдачи ЕГЭ и поступления в ВУЗ мечты на бюджет и, самое главное, для жизни. Я не буду тебя ни в чем убеждать, просто скажу одну вещь… Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил.
Это статистика. Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Что нужно, чтобы сдать наверняка ЕГЭ, поступить в ВУЗ мечты и быть в конечном итоге… более счастливым? Две вещи.
Первое, тебе нужно набить руку, решая задачи
На экзамене у тебя не будут спрашивать теорию. Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка. “Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
И сейчас будет честная реклама наших курсов подготовки к ЕГЭ, потому что они решают обе эти проблемы.
Тебе же понятен этот учебник? Так вот наши курсы такие же понятные как этот учебник.
Потому что их подготовил и ведет автор этого учебника Алексей Шевчук.
Он буквально разжевывает все на вебинарах. Вы решаете задачи. Много задач. У вас будет проверка домашки и марафон «Год за месяц» в мае, чтобы «упаковать» ваши знания и улучшить результат на 20-30%.
Курсы очень бюджетные: от 2000 до 3990 тыс/мес за 12 двухчасовых занятий с Алексеем.
Кликайте по этим кнопкам и читайте условия, там все очень подробно описано:
Гипербола
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Функция заданная формулой \(y=\frac
Определение гиперболы.
График функции \(y=\frac
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=\frac<1>
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: База знаний, Уроки Tag: Гипербола Leave a comment
Что такое гипербола
Понятие гиперболы
Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы выглядит так:
, где a и b — положительные действительные числа.
Кстати, канонический значит принятый за образец.
В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.
Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.
Вспомним особенности математической гиперболы:
Если гипербола задана каноническим уравнением, то асимптоты можно найти так:
Давайте решим несколько примеров, а лучше — приходите тренироваться в детскую школу Skysmart. Ученики решают захватывающие задачки вместе с красочными героями на интерактивной платформе, чертят вместе с учителем на онлайн-доске и не боятся школьных контрольных.
Запишите ребенка на бесплатный вводный урок математики и начните заниматься в удовольствие уже завтра!
Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:
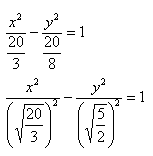
Важно! Без этого шага ветви гиперболы «вылезут» за асимптоты.
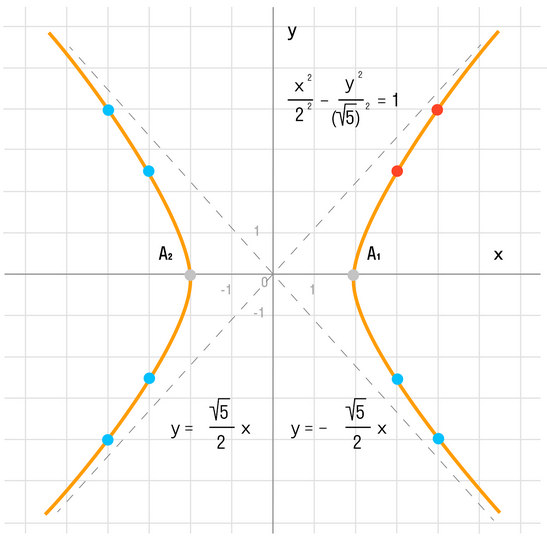
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).
В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.
Способ такой же, как при построении эллипса. Из полученного канонического уравнения
на черновике выражаем:
Уравнение распадается на две функции:
— определяет верхние дуги гиперболы (то, что ищем);
— определяет нижние дуги гиперболы.
Далее найдем точки с абсциссами x = 3, x = 4:
Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.
Действительная ось гиперболы — отрезок А1А2.
Расстояние между вершинами — длина |A1A2| = 2a.
Действительная полуось гиперболы — число a = |OA1| = |OA2|.
Мнимая полуось гиперболы — число b.
В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.
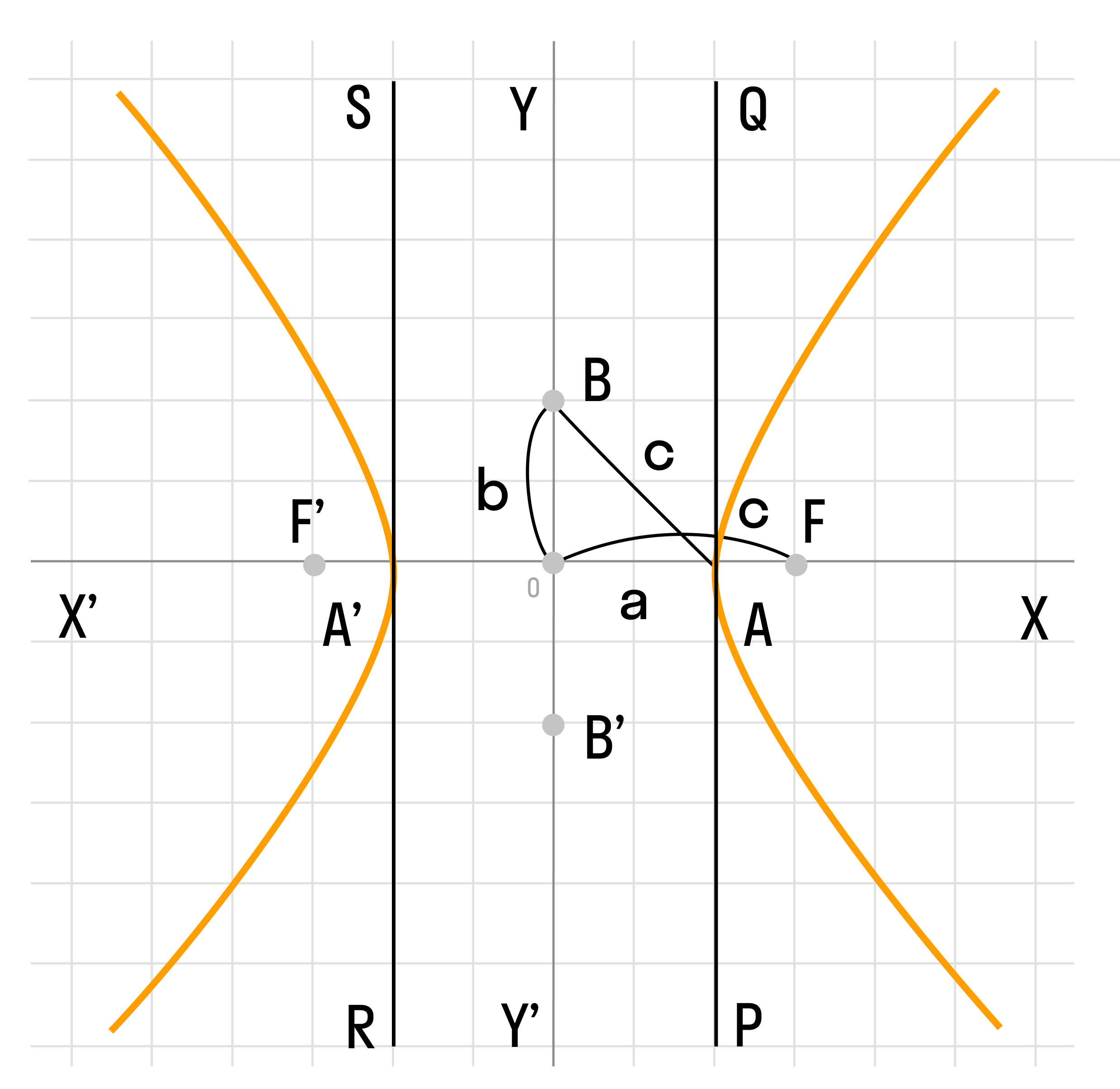
Форма гиперболы
Повторим основные термины и узнаем, какие у гиперболы бывают формы.
Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.
Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.
Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.
Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.
Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.
Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.
Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.
Фокальное свойство гиперболы
Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).
Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:
Рассмотрим, как это выглядит на прямоугольной системе координат:
Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:
Запишем это уравнение в координатной форме:
Избавимся от иррациональности и придем к каноническому уравнению гиперболы:
, т.е. выбранная система координат является канонической.
Директориальное свойство гиперболы
Директрисы гиперболы — это две прямые, которые проходят параллельно оси.
ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.
Директориальное свойство гиперболы звучит так:
Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.
Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
На самом деле для фокуса F2 и директрисы d2 условие
можно записать в координатной форме так:
Построение гиперболы
Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.
Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.
В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:
Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:
Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.
По определению эксцентриситет гиперболы равен
Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.
Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.
Теперь мы знаем, как построить гиперболу. А чтобы знания превратились в практический навык — запишите ребенка на бесплатный вводный урок математики в Skysmart. На занятии покажем, как все устроено, решим пару задачек и дадим рекомендации по программе обучения для вашего ребенка.