Как сделать задачу с дробями
Задачи на дроби
Выражение части в долях целого
Чтобы выразить часть в долях целого, нужно часть разделить на целое.
Задача. В классе 30 учащихся, отсутствуют четверо. Какая часть учащихся отсутствует?
Ответ: В классе отсутствует 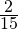
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей, 
Решение: Чтобы найти 
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей, 
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее 
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение числа по его дроби
Для решения задач, в которых требуется найти целое по его части справедливо следующее правило:
Если часть искомого целого выражена дробью, то чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель.
Задача 1. Потратили 50 рублей, это составило 
Решение: Из описания задачи мы видим, что 50 рублей в 6 раз меньше первоначальной суммы, т. е. первоначальная сумма в 6 раз больше, чем 50 рублей. Чтобы найти эту сумму, надо 50 умножить на 6:
Ответ: Первоначальная сумма — 300 рублей.
Задача 2. Потратили 600 рублей, это составило 
Решение: Будем считать, что искомое число состоит из трёх третьих долей. По условию две трети числа равны 600 рублей. Сначала найдём одну треть от первоначальной суммы, а затем сколько рублей составляют три третьих (первоначальная сумма):
Ответ: Первоначальная сумма — 900 рублей.
Второй способ нахождения целого по его части:
Чтобы найти целое по величине выражающей его часть, можно разделить эту величину на дробь, выражающую данную часть.
Задача 3. Отрезок AB, равный 42 см, составляет 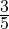
Ответ: Длина отрезка CD 70 см.
Задача 4. В магазин привезли арбузы. До обеда магазин продал 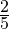
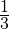
Решение: Сначала узнаем, какую часть от привезённых арбузов составляет число 80. Для этого примем за единицу общее количество привезённых арбузов и вычтем из неё то количество арбузов, которое получилось реализовать (продать):
Итак, мы узнали, что 80 арбузов составляет 

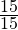
2) 80 : 4 · 15 = 300 (арбузов).
Ответ: Всего в магазин привезли 300 арбузов.
Урок математики в 4-м классе по теме: «Дроби»
формирование знаний, умений, навыков действий с дробями;
развитие памяти логического мышления, воображения, внимания, речи, математических навыков вычисления;
воспитание чувства ответственности, коллективизма, взаимопомощи, аккуратности, самостоятельности, дисциплины, наблюдательности.
Оборудование: модели долей демонстрационная и раздаточная, заготовка-круг, танграмм, схемы задач, таблицы с дробями.
I. Организационный момент.
II. Сообщение темы урока.
– Тема нашего урока. Вот беда. Пропала тема. Никто не видел? Придется вам ее восстановить. Давайте решим примеры, и ответы запишем в порядке возрастания.
Расположить примеры в порядке возрастания ответов и прочесть получившееся слово.
О 12000 : 4000 х 7 х 10 = (210);
Б 720 : 90 x 10 x 8 = (640);
И 90 x 30 : 100 x 1000 = (27000);
На доске появляется название темы: «Дроби».
IV. Постановка цели урока
Сценка “ Буратино на уроке у Мальвины.”
– А сейчас Буратино мы займемся арифметикой.
– Вот вам яблоко (дает). Представьте, что к вам подошел Некто просит поделиться яблоком. Сколько достанется каждому?
– Нисколько! Я не дам Некто яблока, хоть он со мной дерись!
– Буратино, подумайте внимательно. Вам не надо отдавать яблоко, вам надо его поделить. (Буратино думает.)
– Никак не делится. Вот если бы у меня было 2 яблока, то может быть и можно было бы поделить, и то вряд ли, а одно, ну ни как не делится.
– Нет в арифметике такого действия, чтобы одно яблоко на двоих делить.
– Буратино, у вас нет никаких способностей к арифметике. Придется вас отправить в 4 “А” класс. У них как раз это изучают.
– Что, ребята, поможем Буратино?
V. Формирование знаний, умений и навыков.
Нам часто в жизни приходится делить целое на части. Представьте, что к вам пришли гости, а у вас 1 торт. Как быть? Надо делить его поровну. Возьмите на столе модель “торта” (круг).
Учитель показывает, дети повторяют.
К I-у варианту пришло 3 гостя + хозяин. Делим на 4 части. А ко II-у варианту пришло 7 гостей + хозяин. Делим на 8 частей. Разрезаем по линии сгиба на части. Доли получили, а как это записать? С помощью, каких таких знаков? Для звуков мы используем буквы, для записи чисел – цифры, а как записать доли? Доли мы запишем с помощью дробей.
Дробь – это одна или несколько равных долей, записанных с помощью двух натуральных чисел, разделенных чертой
, где – m числитель, а n – знаменатель.
Вывешивается запись на доске, а дети записывают в тетрадь.
– Теперь давайте запишем дроби.
– На сколько частей делили? Записываем под чертой.
– Сколько таких частей взяли? Пишем над чертой.
– На сколько равных частей поделена фигура?
– Сколько частей закрашено?
– Сколько частей незакрашено?
– Как записать с помощью дроби?
3) Закрашивание дробей.
– На сколько частей поделена фигура?
– Сколько надо закрасить?
– Что вам об этом говорит? (Числитель и знаменатель)
– На что указывает числитель дроби? (Сколько частей взято.)
– На что указывает знаменатель дроби? (На сколько частей поделили.)
5) Запись дробей с помощью знака «% «. Запись % с помощью дробей.
6) Сравнение дробей.
1 вариант: возьмите 1/4 часть;
2 вариант: возьмите 1/8 часть;
– У кого больше? Что мы видим?
Дети сравнивают в парах способом наложения. Учитель на модели
Вывод: чем больше знаменатель, при одинаковом числителе, тем меньше дробь, чем меньше знаменатель, при одинаковом числителе, тем больше дробь.
VI. Соревнование по рядам у доски.
Таблицы с дробями вывешиваются на доску. Детям предлагается только поставить знак между парой дробей.
| 1/7 1/10; 1/100 > 1/1000; | 1/4 > 1/5; 1/9 > 1/13; 1/17 2/9; 7/16 > 3/16; 9/2 1 5/40. |
Таблицы с дробями вывешиваются на доску. Детям предлагается только поставить знак между парой дробей.
7) Сложение и вычитание дробей.
Вывод: при одинаковых знаменателях дроби складывают и вычитают как натуральные числа.
Таблицы с дробями вывешиваются на доску. Детям предлагается только записать ответ. От каждого ряда выходят ученики по очереди и записывают ответы. Проверка.
1/8 + 1/4
6/9 + 1/9
7/10 + 3/10
5/15 + 10/15
– Что известно?
– Что надо найти?
– Как найти?
VIII. Самостоятельная работа по рядам.
– Что нового узнали?
– Что такое дробь?
– Какая дробь больше?
– Как складывают и вычитают дроби?
– Сегодня получили оценки 20/4 и 20/5.
Х. Дополнительный материал. Танграмм.
– Определите сколько частей каждого цвета на рисунке и составьте свой рисунок.
Детям раздаются карточки, где изображён с помощью 8 разноцветных треугольников рисунок, и даны отдельно ещё 8 разноцветных треугольников, что бы дети сами составили свой рисунок.
“ Пришел из школы ученик
И папе с мамой говорит:
“Задачку задали у нас,
Ее решал я целый час.
И вышло у меня в ответе
Два землекопа и две трети!”
Решение задач на дроби и проценты
Разделы: Математика
В последние годы понятие «проценты» все чаще встречается в повседневной жизни. Повышение и снижение тарифов на услуги, инфляция, проценты по кредитам, сезонные распродажи- все эти словосочетания, а главное то, что стоит за ними, должны быть понятны каждому, начиная с детского возраста. Очевидно, отвечая требованиям времени, составители вариантов ГИА и ЕГЭ по математике включили задачи на проценты в основную часть заданий. Между тем тема «Проценты. Задачи на проценты» изучается в 6-м классе, а во всех последующих классах проценты появляются периодически в текстовых задачах, вызывая явно отрицательные эмоции у большинства учеников. Большая часть учащихся помнит, что для нахождения процента от числа нужно составить пропорцию и решить ее. Но как составить пропорцию, если в задаче сказано, что во второй день туристы прошли на 20 % меньший путь, чем в первый день, а сколько прошли в первый тоже неизвестно? Для того чтобы справиться с заданием типа В9 в демоверсии ЕГЭ 2009 года, нужно достаточно глубоко разобраться в теме «Задачи на проценты». Как научить детей решать задачи на проценты различного уровня сложности и когда?
На основании собственной практики работы авторам представляется, что использование метода решения задач на дроби и проценты, предложенного в учебнике Г.В.Дорофеева и Л.Г.Петерсон, при определенном изложении материала дает оптимальный результат. О нашем подходе к изучению темы «Задачи на дроби и проценты» и будет рассказано ниже.
На первом уроке темы «Задачи на дроби» в пятом или шестом классе (в зависимости от программы) говорится, что все задачи на дроби делятся на три типа:
Затем каждый тип задач отрабатывается в течение одного-двух уроков по одинаковой схеме. Покажем ее на примере задач первого типа.
Учитель: Мы с вами уже умеем решать задачи, в которых нужно найти какую-то часть от числа. Давайте решим такую: В классе 20 человек. Из них 2\5 девочки. Сколько девочек в классе?
Приходим к правилу: Чтобы найти часть от числа, выраженную дробью, надо это число умножить на дробь.
К задаче составляется схема, по которой ясно видно, какая величина принимается за единицу («целое») и что является ее частью.
Затем каждая следующая задача решается аналогично: составляется схема, вслух проговаривается правило, по нему составляется выражение. Нужно пресекать попытки учащихся решать задачи так, как они решали раньше, т.е. сначала разделить на знаменатель дроби, а затем умножить на числитель. Мы объясняем, что «новый» способ легче для решения более сложных задач. Кроме того, показываем детям аналогию действия по нахождению дробной части числа с действием по нахождению числа в n раз больше данного. Пример: В классе 20 человек. Сколько человек в двух таких классах? 20 умножить на 2. А в трех? 20 умножить на 3. А в 2\5 класса? 20 умножить на 2\5.
Два других типа задач разбираются аналогично. В учебнике Г.В. Дорофеева, Л.Г. Петерсон «Математика 5,часть 2» даны формулировки соответствующих правил и схем к задачам. Затем проводится обобщающий урок по теме. На нем еще раз разбираются все типы задач на примере одной прямой и двух обратных к ней задач. Учитель просит какого-нибудь ученика придумать несложную задачу на нахождение части от числа, выраженной дробью.
Простой пример: В корзине лежало 16 грибов, Из них 3\4 белые. Сколько белых грибов было в корзине? На доске чертится схема, а затем записывается решение в соответствии с нужным правилом.
Теперь учитель предлагает составить задачу другого типа по тем же данным. В случае затруднения он сам произносит текст этой задачи. В корзине лежало 12 белых, что составляет 3\4 всех грибов, лежащих в корзине. Сколько всего грибов было в корзине? Опять составляется схема и записывается решение.
С составлением задачи третьего типа дети обычно уже справляются самостоятельно. В корзине лежало 16 грибов, из них 12 белых. Какую часть всех грибов составляют белые?
На дом задается творческая работа. Каждому ученику нужно самому придумать, записать и красиво оформить 3 задачи: прямую и 2 обратные. Обязательные условия оформления работы:
О чем только не придумываются задачи: часть красных роз в саду и часть «Мерседесов» на автосалоне, часть гнилых помидоров среди купленных и часть золотых монет среди найденного старинного клада. Детская фантазия безгранична. Но практика показала, что дети на годы запоминают придуманные задачи, а заодно и их решения.
В последующем при решении более сложных комбинированных задач на дроби учитель постоянно акцентирует внимание на том, что нужно найти в каждом промежуточном действии, т.е. какой тип задачи и по какому правилу действуем. Правила каждый раз проговариваются вслух. Вспомогательные схемы уже можно не чертить. Постепенно даже слабые ученики усваивают решение задач на дроби, ошибок становится все меньше.
Когда начинается тема: «Проценты. Задачи на проценты», учащимся достаточно четко разъяснить, что проценты – это те же дроби со знаменателем 100.
Снова вспоминаем три типа задач и теперь формулируем правила, как считать:
Формулировка правил, формулы и схемы даны в учебнике «Математика 6, часть 1» тех же авторов.
Задачи всех трех типов опять последовательно отрабатываются на уроках. Снова проводится обобщающий урок по теме «Задачи на проценты», на котором дети вспоминают свои задачи на дроби. Те же три задачи формулируем иначе. В корзине лежало 16 грибов. Из них 75% составляли белые. Сколько белых грибов было в корзине? В корзине лежало 12 белых, что составляло 75% всех грибов, лежащих в корзине. Сколько всего грибов в корзине? И наконец: В корзине из 16 грибов было 12 белых. Какой процент составляют белые от всех грибов в корзине? На дом учащимся опять задается творческая работа. Предлагается переделать свои задачи в задачи на проценты, сохранив по возможности не только условия, но и все числа, переведя дроби в соответствующие проценты. Задачи оформляются по прежним правилам, только без красивых картинок.
В качестве заключительного урока хорошо провести устный зачет. На нем каждый ученик должен ответить одно из правил (кому какое достанется), рассказать условие своей задачи, которую нужно решать, действуя по этому правилу, начертить схему и записать решение.
Далее можно переходить к решению более сложных, комбинированных задач.
Следует обратить внимание на задачи типа: «На сколько процентов 72 меньше, чем 18?». Мы советуем, особенно на первых порах, решать их только со схемами. Кроме того, учащиеся должны твердо усвоить и запомнить, что то, с чем сравнивается, принимается за 100%. Поэтому решение любой задачи нужно начинать с вопроса: «Что мы принимаем за 100%?». Далее чертится схема:
По ней ясно видно, что задачу можно решать двумя способами. Первый способ:
При решении сложных задач на дроби и проценты, на наш взгляд, очень полезно (особенно для сильных учащихся) пытаться решать задачу несколькими способами. Если дети видят эти способы, это значит, что они действуют не автоматически, по заученному правилу, а разбираются в сути задачи.
Большая часть класса, в конце концов, усваивает алгоритмы решения задач различных типов. Поэтому, когда через некоторое время в теме: «Пропорции» начинаем разбирать решение задач на проценты методом пропорции, ученики часто говорят, что им легче «считать по правилам». Но мы объясняем учащимся, что это – еще один способ решения таких задач, который им очень пригодится в будущем на уроках химии.
Практика показала, что благодаря тщательному разбору тем в 5-6 классах: многократному вычерчиванию схем и проговариванию вслух правил, выполнению творческих заданий по составлению прямых и обратных задач разного типа – принципы решения задач на дроби и проценты не только хорошо усваиваются, но и не забываются с годами.
В 7-8 классах при решении текстовых задач достаточно большая часть учащихся может составить математическую модель ситуации, описанной в начале статьи. Если в первый день туристы прошли x км, а во второй на 20% меньше, чем в первый, то x- это 100%- (то с чем сравнивают). А путь во второй день составляет 80% от пути в первый день, т.е. от x, что можно вычислить по правилу нахождения процента от числа и получить 0,8x км.
На факультативных занятиях теми же методами решаются задачи на сплавы и растворы. В 9 классе при подготовке к экзамену по сборнику С.А.Шестакова мы снова вспоминаем три типа задач, схемы и правила их решения, которые теперь записываются в общем виде.
В заключение хочется отметить, что выбранная нами методика вовсе не предполагает работу по программе Г.В.Дорофеева и Л.Г.Петерсон, тем более что она теперь исключена из списка рекомендованных программ. Задачи на дроби и на проценты решаются в 5 и 6 классах при работе по любой программе: Н.Я. Виленкина, С.М. Никольского и др. Просто при изучении данной темы можно воспользоваться предложенным выше методом и соответствующим образом разбирать задачи на уроках математики на протяжении всего курса. Такой подход кажется авторам оптимальным для подготовки учащихся по данной теме.
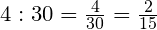
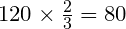


 , где – m числитель, а n – знаменатель.
, где – m числитель, а n – знаменатель.



