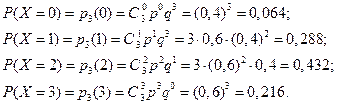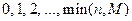Как сделать закон распределения
Формулы: законы распределения случайных величин
В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.
Каталог формул по теории вероятности онлайн
Законы распределения на этой странице
Дискретные случайные величины
Биномиальное распределение ДСВ
| $x_k$ | 0 | 1 | . | k | . | n |
| $p_k$ | $q^n$ | $n\cdot p \cdot q^ | $C_n^k \cdot p^k \cdot q^ | $p^n$ |
Здесь вероятности находятся по формуле Бернулли:
Числовые характеристики биномиального распределения:
Пуассоновское распределение ДСВ
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Ряд распределения по закону Пуассона имеет вид:
| $x_k$ | 0 | 1 | . | k | . |
| $p_k$ | $e^<-\lambda>$ | $\lambda e^<-\lambda>$ | . | $\frac<\lambda^k> | . |
Вероятности вычисляются по формуле Пуассона:
Числовые характеристики для распределения Пуассона:
Геометрическое распределение ДСВ
Формула для вероятностей:
Ряд распределения геометрического закона:
| $x_k$ | 0 | 1 | 2 | . | k | . |
| $p_k$ | $p$ | $q\cdot p$ | $q^2 \cdot p$ | . | $q^k \cdot p$ | . |
Гипергеометрическое распределение ДСВ
$$M(X)=\frac
Непрерывные случайные величины
Показательное распределение НСВ
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Числовые характеристики можно найти по формулам:
Равномерное распределение НСВ
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
Числовые характеристики равномерно распределенной случайной величины:
График плотности вероятностей:
Нормальное распределение или распределение Гаусса НСВ
Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.
Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Числовые характеристики для нормального распределения:
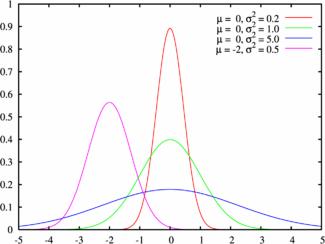
Пример графика плотности распределения для различных значений среднего и СКО:
Функция Лапласа определяется как:
Решенные задачи по теории вероятностей
Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике:
Основные законы распределения
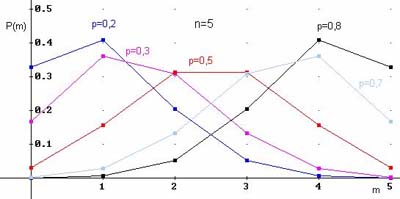
1.Биномиальный закон распределения.
Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.
Например, отдел продаж магазина бытовой техники в среднем получает один заказ на покупку телевизоров из 10 звонков. Составить закон распределения вероятностей на покупку m телевизоров. Построить полигон распределения вероятностей.
2.Геометрическое распределение.
Геометрическое распределение случайной величины имеет следующий вид:
Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей.
3.Гипергеометрическое распределение.
Гипергеометрическое распределение случайной величины имеет следующий вид:
Из таблицы видно, что вероятность угадывания одного числа m=1 выше, чем при m=0. Однако затем вероятность начинает быстро снижаться. Таким образом, вероятность угадывания 4-х чисел уже составляет менее 0,005, а 5-ти ничтожно мала.
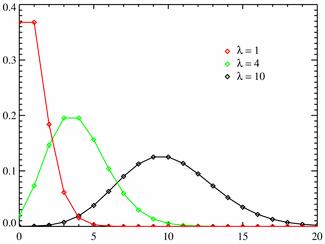
4.Закон распределения Пуассона.
Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид:
Из условия имеем: m=100, λ 1 =8, λ 2 =6, λ 3 =4 ( ≤10 )
(таблица дана не полностью)
Если n достаточно большое и стремится к бесконечности, а значение p стремится к нулю, так что произведение np стремится к постоянному числу, то данный закон является приближением к биномиальному закону распределения. Из графика видно, что чем больше вероятность р, тем ближе кривая расположена к оси m, т.е. более пологая. (Рис.4)
Необходимо отметить, что биномиальный, геометрический, гипергеометрический и закон распределения Пуассона выражают распределение вероятностей дискретной случайной величины.
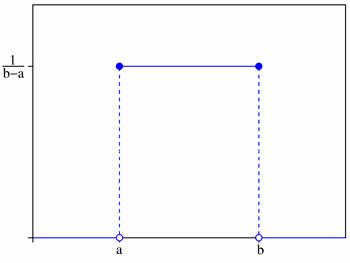
5.Равномерный закон распределения.
Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a,b], то закон распределения называется равномерным. На рис.5 изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения.
6.Нормальный закон распределения (закон Гаусса).
Среди законов распределения непрерывных случайных величин наиболее распрастраненным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид:
График плотности вероятности случайной величины, имеющей нормальный закон распределения, симметричен относительно прямой х=а, т.е х равному математическому ожиданию. Таким образом, если х=а, то кривая имеет максимум равный:
При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины.
Функция, которая выражает распределение случайной величины на интервале (-∞,х), и имеющая нормальный закон распределения, выражается через функцию Лапласа по следующей формуле:
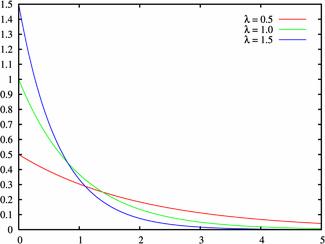
7.Показательный закон распределения.
Закон распределения случайной величины Х называется показательным (или экспоненциальным), если плотность вероятности имеет вид:
График плотности вероятности с параметрами
λ = 2, λ = 4, λ =6 изображен на рис.8
Функция распределения случайной величины Х, которая имеет показательное распределение, имеет вид:
График функции изображен на рис.9
Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:
8.Логарифмически-нормальное распределение.
Если логарифм непрерывной случайной величины изменяется по нормальному закону, то случайная величина имеет логарифмически-нормальное распределение. Функция логаривмически-нормального распределения имеет вид.
Из графика видно, что чем меньше σ и больше математическое ожидание а, тем кривая становится более пологая и больше стремится к симметрии. Данный закон, чаще всего, используется для описания распределения поступления денежных средств (доходов), банковских вкладов, износа основных средств и т.д. (Рис.10)
9. χ ² распределение
Сумма квадратов k независимых случайных величин, которые распределены по нормальному закону, называется χ ² распределением.
χ ² распределение имеет вид:
Плотность вероятности случайной величины, распределенной по распределению χ ² имеет вид:
Из графика видно, что чем больше n=k, тем кривая стремиться к нормальному распределению. Рис.11.
Распределение непрерывной случайной величины называется распределением Стьюдента, если оно имеет вид:
Плотность вероятности распределения Стьюдента имеет вид:
На рис.12 изображена плотность вероятности распределения Стьюдента. Из графика можно увидеть, что чем больше k, тем больше кривая приближается к нормальному распределению.
11. Распределение Фишера-Снедекора.
Распределение случайной величины Фишера-Снедекора имеет вид:
Плотность вероятности случайной величины имеет вид:
При стремлении n к бесконечности распределение Фишера-Снедекора стремится к нормальному закону распределения.(Рис.13)
Закон распределения



Случайной величинойназывают числовую величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретнойназывают случайную величину, которая принимает отдельные, изолированные возможные значения. Непрерывнойназывают случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Законом распределения случайной величиныназывают соответствие между возможными значениями и их вероятностями. Для дискретной случайной величины его можно задать таблично, аналитически (в виде формулы) и графически.
Ряд распределения дискретной случайной величины – это таблица, в первой строке которой перечислены все возможные значения случайной величины, а во второй – вероятности, с которыми она принимает эти значения:
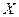 | 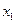 | 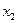 | … | 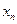 |
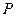 | 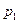 | 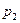 | … | 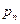 |
Сумма вероятностей должна при этом равняться числу 1.
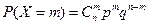
где 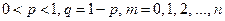
Биномиальный закон распределения представляет собой закон распределения числа наступлений события A в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p.
Пример 30.Составить закон распределения вероятностей числа появлений события А в трех независимых испытаниях, если вероятность появления события в каждом испытании равна 0,6.
Решение. Вероятность появления события в каждом испытании равна 0,6, следовательно, вероятность того, что событие не появится в одном испытании 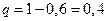
В трех независимых испытаниях событие А может появиться либо 3 раза, либо 2 раза, либо 1 раз, либо совсем не появиться. Таким образом, возможные значения таковы: 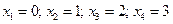
Искомый закон распределения:
| Х | ||||
| Р | 0,064 | 0,288 | 0,432 | 0,216 |
Контроль: 0,216 + 0,432 + 0,288 + 0,064 = 1.
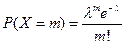
Закон распределения Пуассона является предельным случаем биномиального закона при 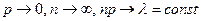
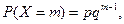
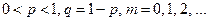
Вероятности 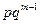
Случайная величина, имеющая геометрическое распределение, представляет собой число m испытаний, проведенных по схеме Бернулли, с вероятностью p наступления события в каждом испытании до первого положительного исхода.
Пример 32.Вероятность поражения цели равна 0,6. Производится стрельба по мишени до первого попадания (число патронов не ограничено). Требуется составить ряд распределения числа сделанных выстрелов.
Решение. Случайная величина X – число сделанных выстрелов – имеет геометрическое распределение с параметром p = 0,6. Ряд распределения X имеет вид:
| Х | … | m | … | |||
| Р | 0,6 | 0,24 | 0,096 | … | 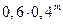 | … |
Дискретная случайная величина X имеет гипергеометрическое распределение, если она принимает значения
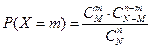
Гипергеометрическое распределение имеет случайная величина X – число объектов, обладающих данным свойством, среди n объектов, случайно извлеченных (без возврата) из совокупности N объектов, M из которых обладают этим свойством.
Пример 33.В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных.
Решение. Случайная величина число стандартных деталей среди отобранных деталей – имеет следующие возможные значения: 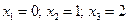
Найдем вероятности возможных значений X:
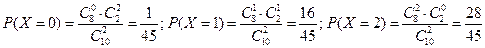
Составим искомый закон распределения:
| Х | |||
| Р | 1/45 | 16/45 | 28/45 |
Контроль: 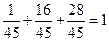
Закон распределения дискретной случайной величины
Закон распределения дискретной случайной величины (ДСВ) представляет собой соответствие между значениями х1, х2,…,хn этой величины и их вероятностями p1, p2,…,pn
Может быть задан аналитически, графически или таблично.
Самый простой способ представления закона распределения дискретной случайной величины — в виде таблицы ряда распределения, то есть
| X | x1 | x2 | …… | xn |
| P | p1 | p2 | …… | pn |
х1, х2,…,хn — значения дискретной случайной величины;
p1, p2,…,pn — вероятности значений X дискретной случайной величина.
Также должно выполняться условия, что сумма вероятностей равна 1, то есть
∑p=p1+p2+ … +pn=1
Графически закон распределения ДСВ задается в виде многоугольника распределения см. здесь., а аналитически, например, с применением формулы Бернулли. Рассмотрим примеры
Пример 1
Монета подбрасывается 10 раз, герб выпал 6 раз, а орел — 4 раза. Составить закон распределения дискретной случайной величины.
Решение
Вероятности равны:
p1(6)=6/10=0,6;
p2(4)=4/10=0,4
| X | 6 | 4 |
| P | 0.6 | 0.4 |
Пример 2
Из корзины извлечено 4 белых шара, 6 черных, 8 синих и 2 красных шара. Найти закон распределения случайной величины X возможного выигрыша на один билет.
Решение
Объем выборки равен
n=4+6+8+2=20
X принимает следующие значения:
x1=4; x2=6; x3=8; x1=2
Найдем их вероятности:
p1(4)=4/20=0,2;
p2(6)=6/20=0,3;
p3(8)=8/20=0,4;
p4(2)=2/20=0,1
Получаем таблицу закона распределения дискретной случайной величины
| X | 4 | 6 | 8 | 2 |
| P | 0.2 | 0.3 | 0.4 | 0.1 |
Пример 3
По контрольной работе по математике школьники получили оценки:
удовлетворительно — 5 человек;
хорошо — 13 человек;
отлично — 7 человек.
Составьте таблицу закона распределения ДСВ
Решение
n=5+13+7=26
| X | 5 | 13 | 8 | 2 |
| P | 0.2 | 0.52 | 0.28 | 0.1 |
Пример 4
Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение
Для составления закона распределения воспользуемся формулой комбинаторики сочетание без повторений, то есть всего 8 изделия, а отобрать необходимо 3 изделия получаем: 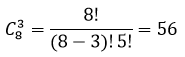
при P(X=0) — вероятность того, что среди трех отобранных изделий не окажется ни одного стандартного;
при P(X=1) — вероятность того, что среди трех отобранных изделий окажется одно стандартное и два нестандартных изделия;
при P(X=2) — вероятность того, что среди трех отобранных изделий окажется два стандартных и одно нестандартное изделие;
при P(X=3) — вероятность того, что среди трех отобранных изделий все три изделия стандартные. 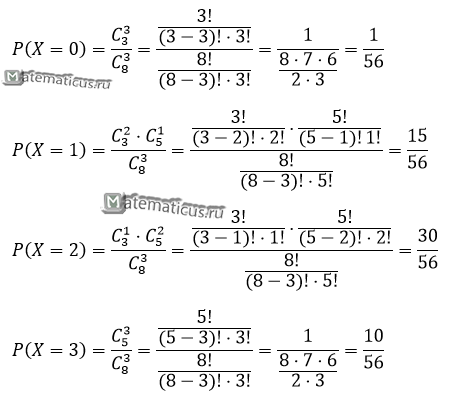
Составим таблицу распределения
| X | 0 | 1 | 2 | 3 |
| P | 0.018 | 0.268 | 0.536 | 0.178 |
Пример 5
В партии из шести деталей имеется четыре стандартных. Наудачу отобраны три детали. Составить закон распределения дискретной случайной величины X — числа стандартных деталей среди отобранных.
Решение
Возможные варианты значений СВ X: 1, 2, 3
$n=C_6^3$ — числу способов, которыми можно выбрать три детали из шести;
$C_4^x$ — число способов, которыми из четырех деталей выбирают х деталей.
$C_2^<3 — x>$ — общее число способов отбора нестандартных деталей
Тогда вероятности события A вычисляются по формуле
Закон распределения дискретной случайной величины X для составления ряда распределения: